树、二叉树和查找等知识点的总结

思维导图

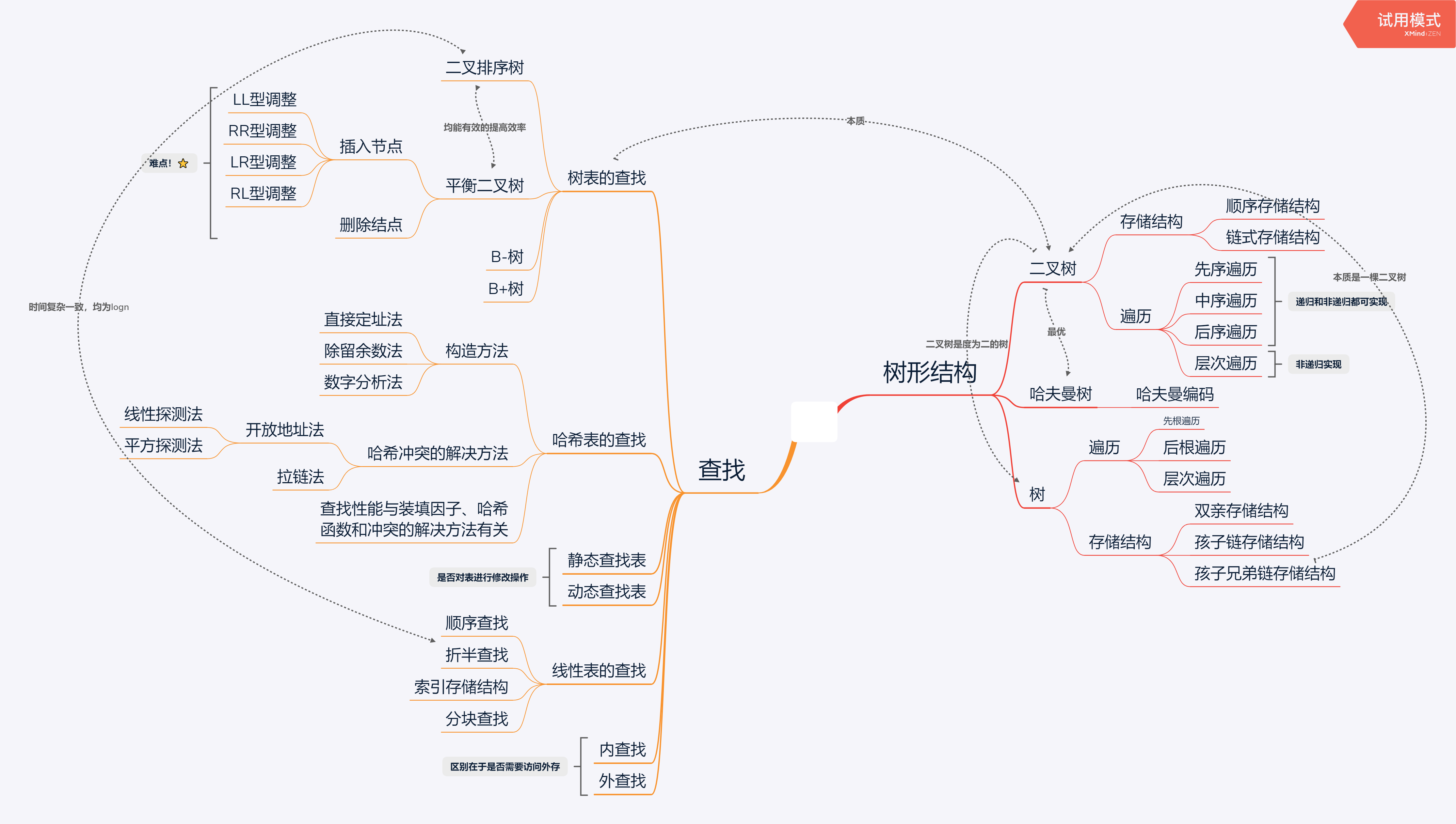
树的存储结构

双亲存储结构

typedef struct 
{
    Elemtype data;
    int parent;       //存放双亲位置
}PTree[MaxSize];

孩子链存储结构

typedef struct node
{
    ElemType data;
    struct node* sons[MaxSize];    //指向孩子结点
}TSonNode;

孩子兄弟链存储结构

typedef struct tnode
{
    Elemtype data;
    struct tnode *hp;    //指向兄弟
    struct tnode *vp;    //指向孩子结点
}TSBNode;

二叉树

存储结构

顺序存储结构

类型声明：

typedef Elemtype SqBSTree[MaxSize];

![image-20200426165155756]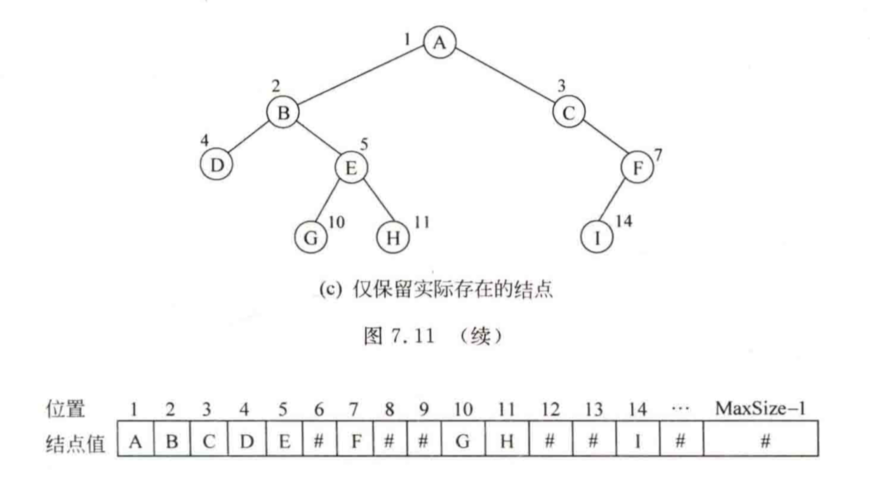

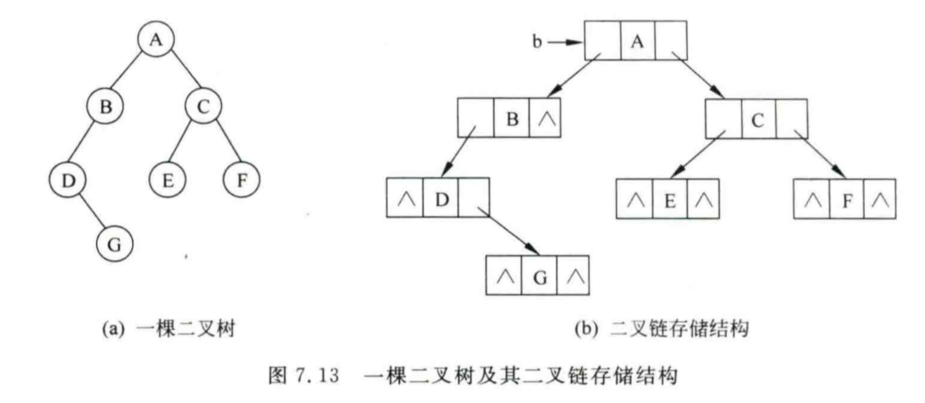
链式存储结构

typedef struct node
{
    ElemType data;
    struct node*lchild;    //指向左孩子节点
    struct node*rchild;    //指向右孩子结点
}BTNode;

基本运算算法实现

创建二叉树（CreateBTree）

void CreateBSTree(BTNode*& b, char* str)
{
	BTNode* St[MaxSize], * p;
	int top = -1, k, j = 0;
	char ch;
	b = NULL;
	ch = str[j];
	while (ch != '')
	{
		switch (ch)
		{
		case'(': top++; St[top] = p; k = 1; break;
		case')': top--; break;
		case',': k = 2; break;
		default:
			p = new BTNode;
			p->data = ch;
			p->lchild = p->rchild = NULL;
			if (b == NULL)
				b = p;
			else
			{
				switch (k)
				{
				case 1:St[top]->lchild = p; break;
				case 2:St[top]->rchild = p; break;
				}
			}

		}
		j++;
		ch = str[j];
	}
}

销毁二叉树(DestroyBTree)

void DestroyBTree(BTNode*& b)
{
	if (!b)
	{
		DestroyBTree(b->lchild);
		DestroyBTree(b->rchild);
		free(b);
	}
}

查找结点(FindNode)

BTNode* FindNode(BTNode* b, ElemType x)
{
	BTNode* p;
	if (b) return NULL;
	else if (b->data == x) return b;
	else
	{
		p = FindNode(b->lchild, x);
		if (p)
			return p;
		else 
			return FindNode(b->rchild, x);
	}
}

求高度(BTHeight)

int BTHeight(BTNode* b)
{
	int lchildh, rchildh;
	if (b == NULL)return (0);
	else {
		lchildh = BTHeight(b->lchild);
		rchildh = BTHeight(b->rchild);
		return (lchildh > rchildh) ? (lchildh + 1) : (rchildh + 1);
	}
}

二叉树的遍历

先序遍历

访问根结点->先序遍历左子树->先序遍历右子树

中序遍历

中遍历左子树->访问根结点->中序遍历右子树

后序遍历

后遍历左子树->后序遍历右子树->访问根结点

代码实现：(递归实现)

/*先序递归遍历*/
void PreOrder(BiTree b)
{
	if (b != NULL)
	{
		cout << b->data;
		PreOrder(b->lchild);
		PreOrder(b->rchild);
	}
	else return;
}

/*中序遍历*/
void InOrder(BiTree b)
{
	if (b != NULL)
	{
		InOrder(b->lchild);
		cout << b->data
		InOrder(b->rchild);
	}
	else return;
}

/*后序遍历*/
void PostOrder(BiTree b)
{
	if (b != NULL)
	{
		PostOrder(b->lchild);
		PostOrder(b->rchild);
		cout << b->data;
	}
	else return;
}

层次遍历(非递归实现)

void LevelOrder(BTree T)
{
	if (T == NULL)
	{
		return;
	}
	queue<BTree>Q;
	BTree BT;
	Q.push(T);
	int flag = 0;    //定义个标志，使输出第一个元素前不带空格
	while (!Q.empty())
	{
		if (flag == 0)
		{
			flag = 1;
		}
		else
		{
			cout << " ";
		}
		BT = Q.front();
		Q.pop();
		cout << BT->data;
		if (BT->lchild != NULL)
		{
			Q.push(BT->lchild);
		}
		if (BT->rchild != NULL)
		{
			Q.push(BT->rchild);
		}

	}
	return;
}

哈夫曼树

结点类型：

typedef struct
{
    char data;
    double weight;    //权重
    int parent;
    int lchild;
    int rchild;
}

查找

折半查找

折半查找又称二分查找，它是一种效率较高的查找方法。但是折半查找的要求线性表是有序表。折半查找的查找过程如图：

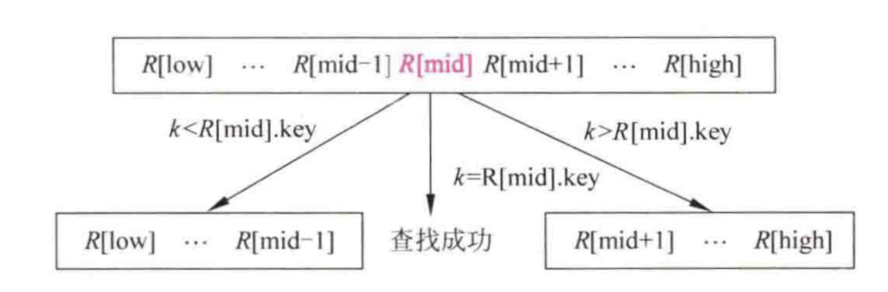
算法实现：

int BinSearch(ReeType R[], int n, KeyType k)     //R为有序表R[0,n-1]
{
	int low = 0;
	int high = n - 1;
	int mid;
	while (low <= high)
	{
		mid = (low <= high) / 2;
		if (k == R[mid].key)
			return mid + 1;
		if (k < R[mid].key)
			high = mid - 1;
		else
			low = mid + 1;
	}
	return 0;
}

ASL计算

假设如此一棵判定树，在查找成功时会找到图中某个内部结点，在查找不成功时会找到图中某个外部结点

[ASL_{成功}=frac {1*1+2*2+4*3+4*4}{11}=3 ]

[ASL_{不成功}=frac {4*3+8*4}{12}=3.67 ]

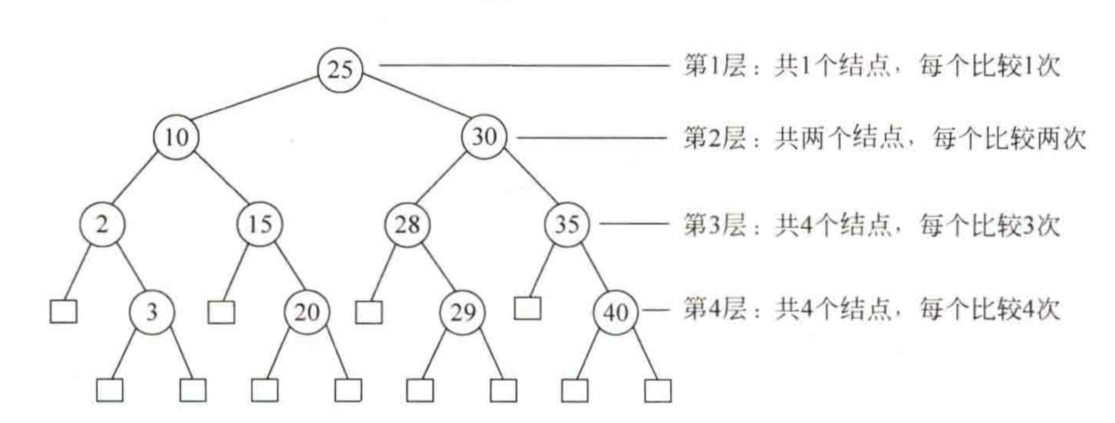
二叉排序树

定义

二叉排序树又称二叉搜索树，它或者是空树或者是满足如下条件的树：

若根节点的左子树非空，则左子树上的所有结点关键字均小于根结点的关键字；
若根节点的右子树非空，则右子树上的所有结点关键字均大于根结点的关键字；
根结点的左右子树本身又各是一棵二叉排序树。

声明节点类型

typedef struct node
{
    KeyType key;
    InfoType data;
    struct node*lchild,*rchild;
}BSTNode;

疑难点解决

二叉树与树、森林之间的转换

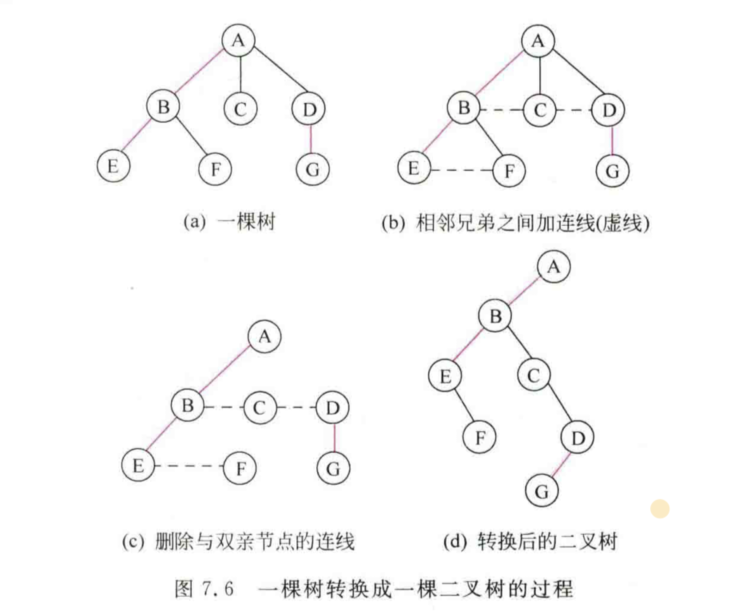
树转换为二叉树

过程如下：

树中所有相邻兄弟之间加一条连线；
对树中的每个结点只保留它与长子之间的连线，删除与其他孩子之间的连线
以树的根结点为轴心，将整棵树顺时针转动45°，使之结构层次分明。

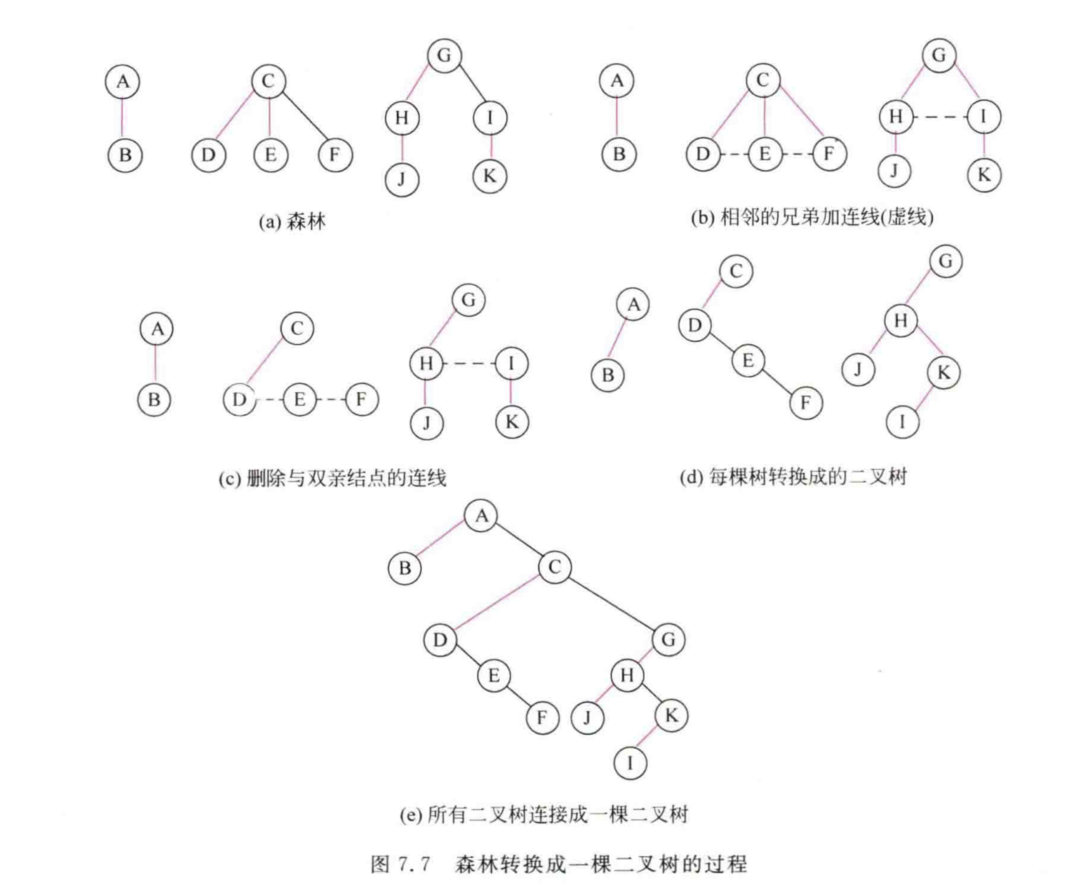
森林转换为二叉树

过程如下：

将森林中每棵树转换成相应的二叉树。
第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的左孩子结点，当所有二叉树连在一起后，此时得到的二叉树就是森林转换得到的二叉树。

二叉树还原为树或者森林

过程如下：

若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子等都与该结点的双亲结点用连线连起来。
删除原二叉树中所有双亲结点与右孩子结点之间的连线。
整理由前面两步得到的树，即以根结点为轴心，逆时针转动45°，使之结构层次分明。

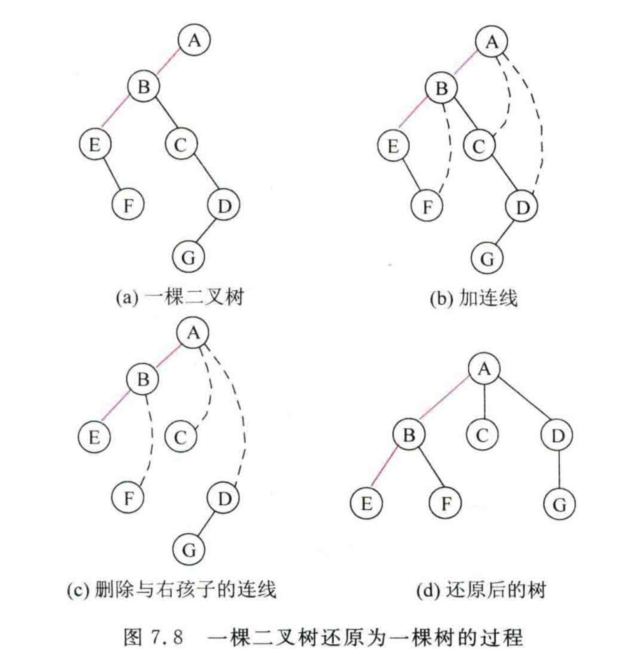
（实际上，二叉树的还原就是将二叉树中的左分支保持不变，将二叉树中的右分支还原成兄弟关系）

平衡二叉树的插入结点

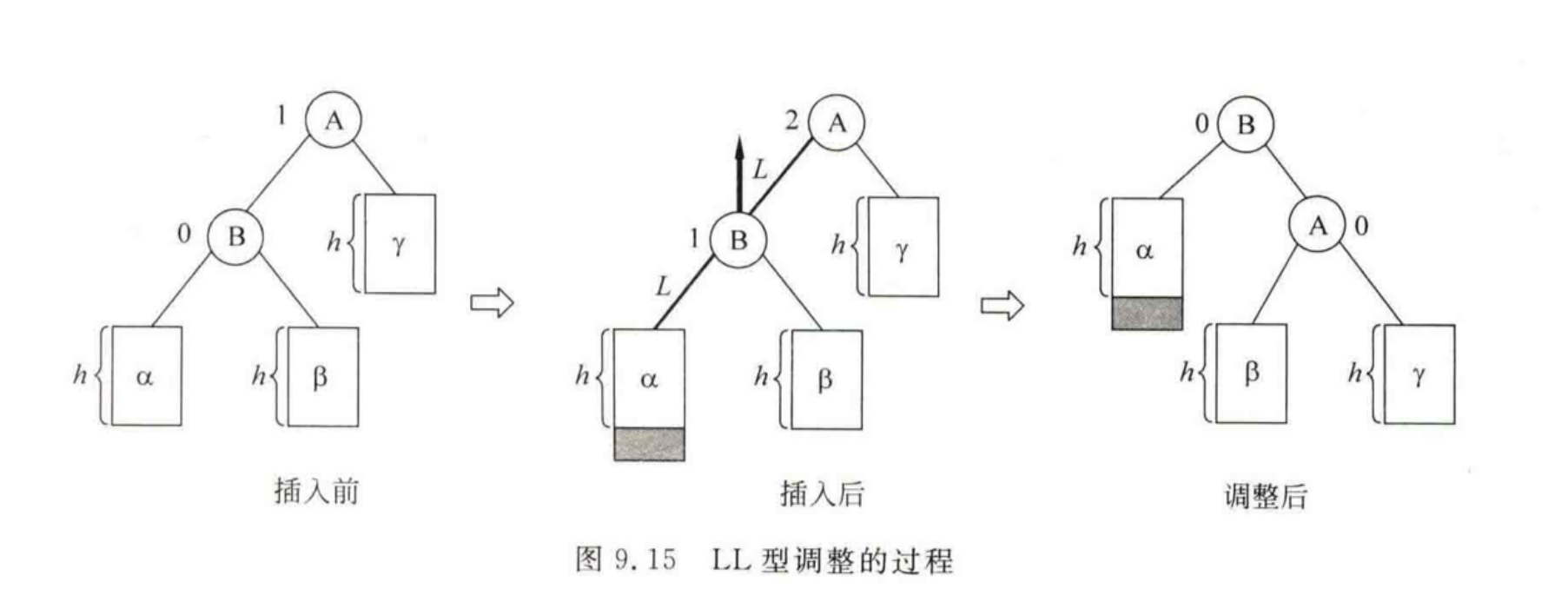
LL型调整

将B结点向上升替代A结点成为根结点，A结点作为B结点的右孩子，而B结点的原右子树β作为A结点的左子树。
RR型调整

将B结点向上升替代A结点成为根结点，A结点作为B结点的左孩子，而B结点的原左子树β作为A结点的右子树。
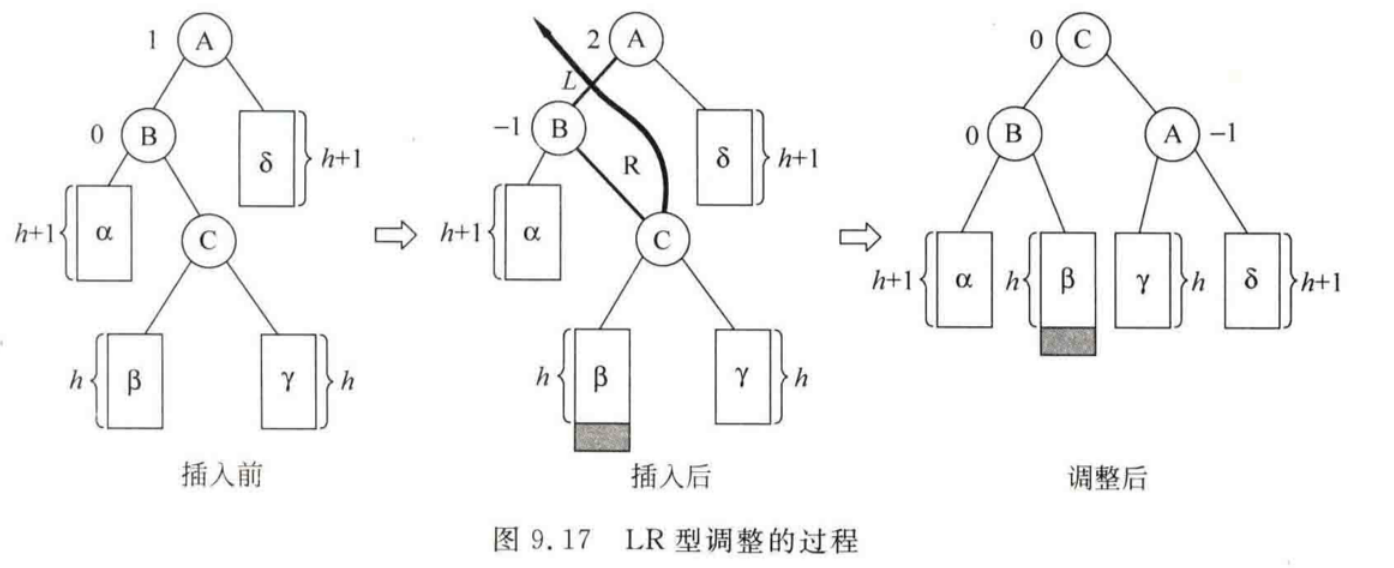
LR型调整

将C结点向上升作为为根结点，B结点作为C结点的左孩子，A结点作为C结点的右孩子，而C结点的原左子树β作为B结点的右子树，而C结点的原右子树γ作为A结点的左子树。
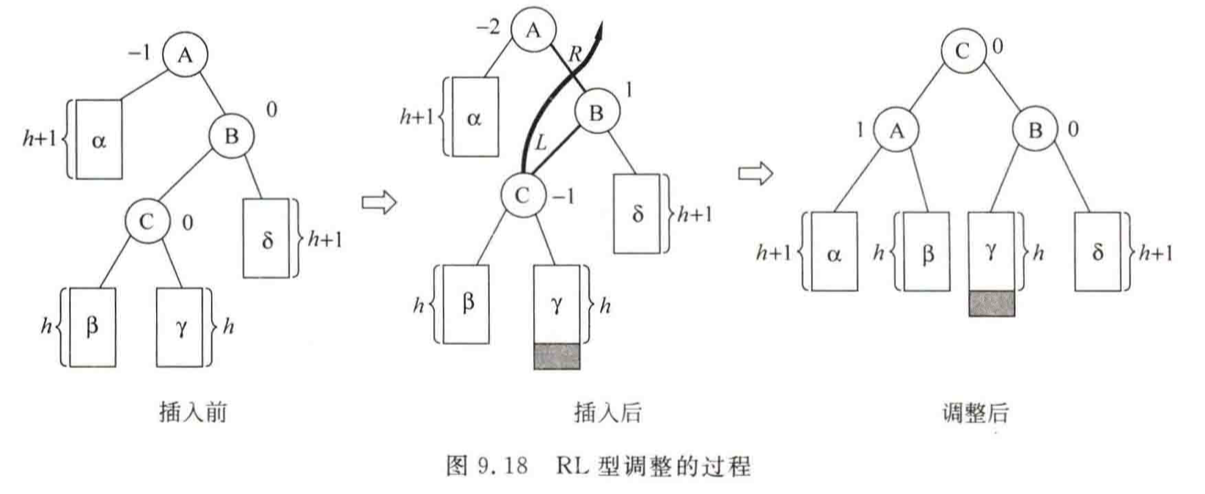
RL型调整

将C结点向上升作为为根结点，A结点作为C结点的左孩子，B结点作为C结点的右孩子，C结点的原左子树β作为A结点的右子树，而C结点的原右子树γ作为B结点的左子树。

平衡二叉树的删除结点

过程如下：

查找。先在平衡二叉树中查找到关键字为k的结点p。
删除。删除p结点分为一下几种情况：

1）叶子结点：直接删除该结点。

2）单分支结点：用该结点的左或右孩子代替该结点。

3）双分支结点：用该结点的中序前驱结点替换待删除的结点的值，再删去前驱结点。
调整。若删除的是结点q，则从结点q向根结点方向查找第一个失去平衡的结点；

1）若所有结点都是平衡的，则不需要调整。

2）假设找到某个平衡因子为-2：其右孩子的平衡因子是-1，则作RR型调整；其右孩子的平衡因子是1，则作RL型调整；其右孩子的平衡因子是0，则作RR型或RL型调整均可。

3）假设找到某个平衡因子为-2：其左孩子的平衡因子是-1，则作LR型调整；其右孩子的平衡因子是1，则作LL型调整；其右孩子的平衡因子是0，则作LR型或LL型调整均可。