动态规划算法：0/1背包问题 (0/1 Knapsack Problem)

一、问题描述

给定一堆物品，其重量是一个一维数组 wt，其对应的价值为另一个一维数组 vals。

给你一个背包，背包容量为w，如何选择物品，使其最后累加的重量不超过背包容量，同时价值最大。(每种重量的物品只有一件)

0/1的意思是，每件物品只有选择或不选择两种状态，而不能拆分物品的重量。

二、状态分析

假设给定的数值分别为： wt = {1, 3, 4, 5}; vals = {1, 4, 5, 7}; w = 7

设二维数组 c[i][j] 表示前 i 个物品放入容量为 j 的背包，所获得的最大价值

这里我们需要对几种情况进行讨论

1. 如果当前的物品重量大于背包的容量，即wt[i] > j，此时物品不能放入背包中，所以此时 c[i][j] 等于取前一次物品放入容量为j的背包时的值，即

c[i][j] = c[i-1][j]

2. 当wt[i] <= j 时，表示当前物品可以放入背包中，但你还是可以选择不放入，

所以在这里我们需要对放入与不放入进行判断，判断是放入产生的价值大还是不放入产生的价值大

当选择不放入时此时的价值为 c[i-1][j]；当选择放入时价值为：当前物品的价值vals[i] + 当前背包总重量减去当前物品重量后剩余背包空间所能产生的最大价值c[i-1][j-wt[i]]

取 c[i-1][j-wt[i]] 而非 c[i][j-wt[i]] 原因在于每一样物品只能放一次

我们需要在这两个值之间取产生的价值最大的

c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i])

所以上面的式子即我们需要的状态转移方程。

如果没看懂，没关系。我下面再通过对具体例子一步步分析，看这个式子为什么是这样子的

首先我们设置一个二维数组，如图，横坐标表示取到当前的物品，纵坐标表示背包容量，每个二维数组的值表示取当前坐标时背包对应的价值。

我们需要定义一些初值，当背包容量或者物品价值为0时，获得的价值都为0

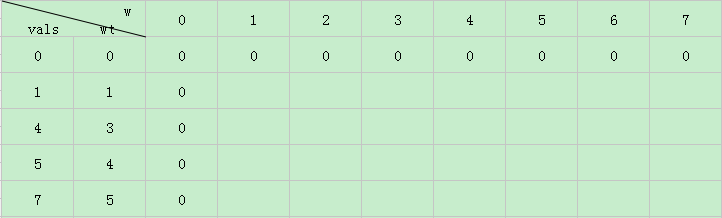
我们来看第一行

1. 当 j = 1 时，wt <= j，所以我们需要判断 c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(0, c[i-1][0] + 1) = 1，所以此处应填入1；

2. 当 j = 2 时，与前面一样判断 c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(0, c[i-1][1] + 1) = 1，填入1；

之后同理可以得到第一行的数据为

接着来看第二行

1. 因为第二行的 wt = 3，所以所有小于3的背包都不能装此时的物品，所以根据状态转移方程 c[i][j] = c[i-1][j]

2. j = 3 时，判断 c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(1, c[i-1][0] + 4) = 4

3. j = 4 时，c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(1, c[i-1][1] + 4) = 5

之后同理可得这行的数据如图

第三行，此时 wt = 4

1. 按照之前分析一样，当 j < 4 时，c[i][j] = c[i-1][j]

2. j = 4 时，c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(5, c[i-1][0] + 5) = 5

3. j = 5 时，c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(5, c[i-1][1] + 5) = 6

4. j = 6 时，c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(5, c[i-1][2] + 5) = 6

5. j = 7 时，c[i][j] = max(c[i-1][j], c[i-1][j - wt[i]] + vals[i]) = max(5, c[i-1][3] +5) = 9

如此，得到第三行的值为

同理可以得到最终的表格如下图

所以此二维数组最后一个值即为之后的结果：9

三、程序实现

public class Knapsack
{
    public int solution(int[] vals, int[] wt, int w)
    {
        int[][] c = new int[vals.length + 1][w + 1];

        for(int i = 0; i <= vals.length; i++)
        {
            for(int j = 0; j <= w; j++)
            {
                if(i == 0 || j == 0)
                {
                    c[i][j] = 0;
                    continue;
                }

                if(wt[i - 1] <= j)
                {
                    c[i][j] = Math.max(c[i-1][j], c[i-1][j - wt[i-1]] + vals[i-1]);
                }
                else
                {
                    c[i][j] = c[i-1][j];
                }
            }
        }

        return c[vals.length][w];
    }

    public static void main(String[] args)
    {
        int[] vals = {1, 4, 5, 7}, wt = {1, 3, 4, 5};
        int w = 7;
        Knapsack k = new Knapsack();
        System.out.println(k.solution(vals, wt, w));
    }
}

结果为