定义:给定正整数n,小于等于n的正整数之中,有多少个数与n互质
计算个数的公式 欧拉函数,φ(n)表示
欧拉函数证明:
1. n = 1, φ(1) = 1 。1与任何数(包括自身)互质
2. n为质数, φ(n)=n-1 。质数n与小于n的数互质(除了自身)
3. 如果n是质数的次方 n = p^k ( p 为质数,k 为大于等于1的整数)。

因为为p(质数)的k次方,则n的因子只有 p 。
小于(p^k)的数有(p^k - 1)个
所以p的倍数与n皆有(1,p)两个因子,除了p的倍数,其他数都与n互质
所以小于n的数中为p的倍数的个数为:(p^k)/p - 1
所以 φ(n) = (p^k - 1) - ((p^k)/p - 1)
= p^k - p^k)/p
= p^k - p^(k-1)
= p^k(1 - 1/p)
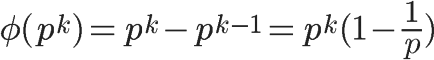
4. n = p * q (p, q互质)
φ(n) = φ(p*p) = φ(p)*φ(q)
5. 任意大于1的n
n可以写成多个质数次方的积




直接求n的欧拉函数φ(n)

ll Euler(ll n) { ll ans = 1; ans = ans * n; for(ll i = ; i * i <= n; i++) { if(n % i == 0) ans = ans / i * (i - 1); while(n % i == 0) n /= i; } if(n > 1) ans = ans / n * (n - 1); return ans; }
欧拉函数线性筛法证明:
性质:H(x * p) = H( x ) * (p - 1) / p
以下p均为素数情况下求取欧拉函数(所以线性筛法与素数筛法结合)
1. phi( p ) = p - 1
2. phi( p ^ k ) = p ^ k * (1 - 1 / p) = (p - 1) * p ^ (k - 1)
3. if( i % p == 0), phi( i * p ) = p * phi( i );
φ( i ) = i * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr)
因为 i 是 p 的倍数,且p为素数
φ( i * p ) = i * p * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr)
= p * i * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr)
= p * φ( i )
4. if( i % p != 0), phi( i * p ) = ( p - 1 ) * phi( i );
φ( i ) = i * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr)
因为 i 不是 p 的倍数,且p为素数,所以
φ( i * p ) = i * p * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr) * (1 - 1/p)
= i * (1-1/p1) * (1 - 1/p2)...(1 - 1/pr) * (p - 1)
= (p - 1) * φ( i )
欧拉函数φ(n)的线性筛法,求1 - n 中的欧拉值

1 const int maxn = 1e8; 2 int phi[maxn], prime[maxn], vis[maxn]; 3 int n, cnt = 0; 4 void getphi(int n) 5 { 6 memset(vis, 0, sizeof(vis)); 7 phi[1] = 1; 8 for(int i = 2; i <= n; i++) 9 { 10 if(!vis[i]) //i是素数 11 { 12 prime[++cnt] = i; 13 phi[i] = i - 1; 14 } 15 for(int j = 1; j <= cnt; j++) 16 { 17 if(i * prime[j] > n) 18 break; 19 vis[i*prime[j]]= 1; 20 if(i % prime[j] == 0) 21 { 22 phi[i*prime[j]] = prime[j] * phi[i]; 23 break; 24 } 25 else 26 { 27 phi[i*prime[j]] = (prime[j]-1) * phi[i]; 28 } 29 30 } 31 } 32 }
