计算几何二维几何前置基础知识

内容参考书籍——《算法竞赛入门经典训练指南》

　　在平面坐标系下，向量和点一样用两个数，x和y表示。判断相等使用“三态函数”dcmp，减少精度问题。另外，向量有一个所谓的“极角”，即从x轴正半轴旋转到该方向所需的角度。c标准库里的atan2函数就是用来求极角的，例如：向量（x,y）的极角就是atan2(y,x)(单位：弧度)。

　　点积，高中知识。

　　叉积。简单地说，两个向量的叉积等于两个向量组成的三角形的有向面积的两倍。(图中带箭头的向量为v，和v同一个起点的另外一条向量为w，忘记标v和w了尴尬)

         cross（v,w）>0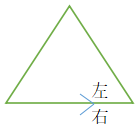                   cross(v,w)<0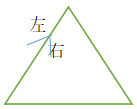 

 　　顺着第一个向量v看，，如果w在左边，那么v和w的叉积大于0，否则小于0.如果两个向量共线（方向相同），那么叉积等于0（三角形退化成为线段）。不难发现，叉积不满足交换律。事实上，cross(v,w)=-cross(w,v)。在坐标系下，两个向量的叉积等于x_Ay_B-x_By_A。

　　位置。当我们把叉积和点积组合在一起时，我们便可以细致地判断两个向量的位置关系。第一个向量v总是水平向右的，那么另外一个点就可以用这样的方式确定位置关系（点积符号，叉积符号）。例如，当w在第二象限时点积为负但叉积均为正，用（-,+）表示。

　　旋转。向量可以绕起点旋转，公式为x^，= xcosa-ysina , y^，= xsina+ycosa。其中a为逆时针旋转的角。

　　单位法线。旋转90°后把长度归一化即可。

　　以上内容采用如下代码实现：

struct Point
{
    double x,y;
    Point(double x=0, double y=0):x(x),y(y) {}//构造函数，方便编写代码
};
typedef Point Vector;//别名
//向量+向量=向量，点+向量=点
Vector operator + (Vector A, Vector B){return Vector(A.x+B.x,A.y+B.y);}
//点-点=向量
Vector operator - (Vector A, Vector B){return Vector(A.x-B.x,A.y-B.y);}
//向量*数=向量
Vector operator * (Vector A, double p){return Vector(A.x*p,A.y*p);}
//向量/数=向量
Vector operator / (Vector A, double p){return Vector(A.x/p,A.y/p);}

bool operator < (const Point& a, const Point& b){return a.x<b.x||(a.x==b.x&&a.y<b.y);}

const double eps = 1e-10;
int dcmp(double x)
{
    if (fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}

bool operator == (const Point& a, const Point &b){return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;}

//计算点积、向量长度、夹角函数
double Dot(Vector A, Vector B){return A.x*B.x+A.y*B.y;}
double Length(Vector A){return sqrt(Dot(A,A));}
double Angle(Vector A, Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}

//计算叉积
double Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
double Area2(Point A, Point B, Point C){return Cross(B-A,C-A);}

//计算旋转和单位法向量
//rad为弧度
Vector Rotate(Vector A, double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));}
Vector Normal(Vector A)
{
    double L =Length(A);
    return Vector(-A.y/L,A.x/L);
}

　　下面是2019.9.24更新

　　点和直线。采用参数方程表示直线(参数方程在表示直线，线段，射线时其方程的区别仅仅在于参数，射线t>0，线段在0-1之间，直线无限制) 。直线用直线上一点P₀和方向向量v表示，则直线上所有点P满足P=P₀+tv，其中t为参数。如果已知直线上两不同点A和B，则方向向量为B-A，所以参数方程为A+(B-A)t。

　　直线交点。设直线为P+tv和Q+tw，设向量u=P-Q，交点在第一条直线的参数为t₁，在第二条直线上的参数为t₂，则交点的x和y可以列出一个方程，解得：

\[{t_1} = \frac{{cross\left( {w,u} \right)}}{{cross\left( {v,w} \right)}},\quad {t_2} = \frac{{cross\left( {v,u} \right)}}{{cross\left( {v,w} \right)}}\]

此处需要注意的是，从上述公式可以看到在精度要求极高的情况下需要自定义分数类。

　　点到直线的距离。利用叉积计算，即平行四边形的面积除以底。

　　点到线段的距离。分两种可能：该点的投影在线段上和不在线段上。若P点的投影在线段(AB)上(Q)则距离为PQ；若不在线段上，则所求距离为PA否则为PB。判断Q的位置可以用前文提到的（点积符号，叉积符号）进行判断。

　　点的投影。尽管上面的方法避免了求投影点Q，但是有些时候我们不得不求出投影点Q。为此，我们把直线AB写成参数式A+tv(v为向量AB)，并且设Q的参数为t₀，那么Q=A+t₀v，接下来解出t₀就能得到Q点，根据PQ垂直于AB，两个向量的点积应该为0，因此Dot(v,P-(A+t₀v))=0。根据分配律，有：Dot(v,P-A)-t₀*Dot(v,v)=0，这样便解出t₀，从而得到Q点。

　　线段相交。判定两线段是否相交，我们定义“相交规范”为两线段恰好有一个公共点，且不在任何一条线段的端点。其充要条件为：每条线段的两个端点都在另一条线段的两侧(这里的“两侧”是指叉积的符号不同)。

　　如果允许在端点处相交呢？那么，情况就比较复杂了，c1和c2不都是0，表示两线段共线，这时可能还会出现部分重叠的情况哦~如果c1和c2不都是0，则只有一种相交方法，即某个端点在另外一条线段上。为了判断上述情况是否发生，还需要判断一个点是否在一条线段上(不包含端点)，见代码。

　　多边形有向面积。如果多边形是凸的，可以从第一个顶点出发，把凸多边形分成n-2个三角形，然后把面积加起来。事实上这个方法对非凸多边形也适用，因为三角形的面积是有向的，在外面的部分可以正负抵消。

　　取P[0]点为划分顶点，一方面可以少算两个叉积(0和任意向量的叉积都等于0)，另一方面也减少了乘法溢出的可能性，还不用特殊处理(i=n-1的时候，下一个顶点是P[0]而不是P[n]，因为P[n]不存在)。

　　更新内容代码如下：

//交点，注意精度问题
//调用该函数前请确保两条直线P+tv和Q+tw有唯一交点。当且仅当Cross(v,w)非0
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w)
{
    Vector u = P-Q;
    double t = Cross(w,u) / Cross(v,w);
    return P+v*t;
}
//点到直线的距离。用叉积计算。平行四边形的面积除以底
double DistanceToLine(Point P, Point A, Point B)
{
    Vector v1 = B-A,v2= P-A;
    return fabs(Cross(v1,v2)) / Length(v1);
}
//点到线段的距离
double DistanceToSegment(Point P, Point A, Point B)
{
    if (A==B) return Length(P-A);
    Vector v1 = B-A,v2 = P-A,v3=P-B;
    if (dcmp(Dot(v1,v2))<0) return Length(v2);
    else if (dcmp(Dot(v1,v3))>0) return Length(v3);
    else return fabs(Cross(v1,v2)) / Length(v1);
}
//计算投影点
Point GetLineProjection(Point P, Point A, Point B)
{
    Vector v = B-A;
    return A+v*(Dot(v,P-A) / Dot(v,v));
}
//按“相交规范”判断相交
bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2)
{
    double c1 = Cross(a2-a1,b1-a1),c2 = Cross(a2-a1,b2-a1),
    c3 = Cross(b2-b1,a1-b1),c4 = Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
//允许在端点处相交，判断是否发生加入下面一段判断一个点是否在一条线段上的代码
bool OnSegment(Point P,Point a1, Point a2)
{
    return dcmp(Cross(a1-P,a2-P)) == 0 && dcmp(Dot(a1-P,a2-P))<0; 
}
//多边形的有向面积
double PolygonArea(Point* p, int n)
{
    double area = 0;
    for (int i = 1; i < n-1; ++i)
    {
        area +=Cross(p[i]-p[0],p[i+1]-p[0]);
    }
    return area/2;
}