参考: LLE原理总结
个人理解
PCA 降维的缺陷:高维空间各个样本之间存在一些线性关系,降维之后并没有保留这些关系。比如,在高维空间中,其最短路径并不是三维空间中的两点之间直线最短,而是如下图的曲面距离,而我们降维后,就变成了投影距离。
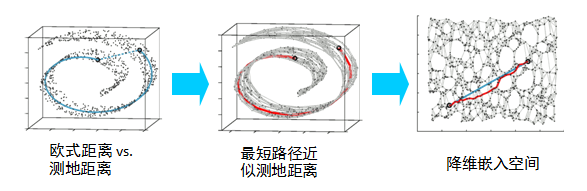
因此,我们希望能够保留原空间的距离(只是一个例子),如下图,是将原曲面展开,而不是直接投影到平面中。
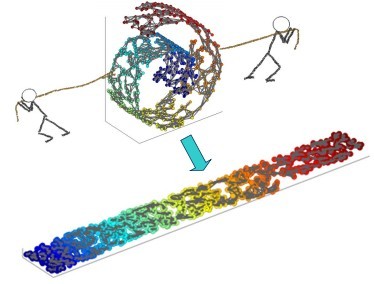
LLE 算法:
与 PCA 不同的是,LLE 保留了高维空间的局部线性关系。
LLE在降维之前,先训练出每个样本与其最近的k个样本的线性关系——weights,再把该线性关系套用在降维空间后的每个样本。
补充
【关于降维/冗余】
如何理解冗余?
如二维平面上,y=x 附近的数据点有很强的线性相关性,也就是说其中一维是冗余的,我们只要知道其中一维,就可以推出另一维,因此可以进行降维,对于本例可以进行平移+旋转,使其分布在x轴上。
如何用数学来表示这种思想?
方差/协方差最大化,即投影后的点之间方差最大。方差和协方差的关系:当数据点归一化和中心化后,二者最大化的方法是等价的,一般直接求协方差的最大化。具体参考链接的公式推导。
【kernel PCA】
假设K是已知的。
与上面的一样,我们同样要求协方差的最大化,
[egin{align}
C&=sum_{i=1}^{N}phi(x_i)phi(x_i^T)\
&=[phi(x_1),...,phi(x_N)]egin{bmatrix}phi(x_1)^T\...\phi(x_N)^Tend{bmatrix}\
&=X^TX\
end{align}
]
但是,Φ是未知的,或者难以计算的,因此我们设法借助核函数来求解.
[egin{align}
K&=XX^T\
&=egin{bmatrix}phi(x_1)^T\...\phi(x_N)^Tend{bmatrix}[phi(x_1),...,phi(x_N)]\
&=egin{bmatrix}phi(x_1)^Tphi(x_1) &... &phi(x_1)^Tphi(x_N)\
...&...&...\
phi(x_N)^Tphi(x_1)&...&phi(x_N)^Tphi(x_N)end{bmatrix}\
&=egin{bmatrix}K(x_1,x_1) &... &K(x_1,x_N)\
...&...&...\
K(x_N,x_1)&...&K(x_N,x_N)end{bmatrix}
end{align}
]
【注意】这里的K=XXT和要求的协方差XTX并不相等,但二者肯定存在某种关系:
[egin{align}
XX^Tu&=lambda u&u为单位化的特征向量\
X^TX(X^Tu)&=lambda (X^Tu) &X^Tu为特征向量,但不一定是单位化的\
end{align}
]
因此,要对特征向量X^Tu单位化:
[v=frac{X^Tu}{||X^Tu||}=frac{X^Tu}{sqrt{u^TXX^Tu}}=frac{X^Tu}{sqrt{u^Tlambda u}}=frac{X^Tu}{sqrt{lambda}}\
其中,u^Tu=1,v可以看作一个方向轴/维度\
记alpha=frac{u}{sqrt{lambda}},为一个列向量v,所以:v=sum_{i=1}^{N}alpha_iphi(x_i)
]
但是,X^T仍然是未知的,所以v也是未知的,即高维度的特征空间的方向轴未知,但是,我们可以直接求Φ(xj)在特征空间v方向上的投影(这才是我们最终目的):
[egin{align}
v^Tphi(x_j)&=frac{u^TXphi(x_j)}{sqrt{lambda}}\
&=frac{u^T}{sqrt{lambda}}egin{bmatrix}phi(x_1)^T\...\phi(x_N)^Tend{bmatrix}phi(x_j)\
&=frac{u^T}{sqrt{lambda}}egin{bmatrix}K(x_1,x_j)\...\K(x_N,x_j)end{bmatrix}
end{align}
]
因此,我们只要求出核函数的特征值及其对应的单位特征向量,就可以得到高维空间的投影。