这篇博客主要介绍一种最优化的方法:牛顿法,拟牛顿法的两种实现(DFP 和 BFGS)。
牛顿法
牛顿法是一个寻找方程根的算法,迭代计算的过程如图所示。这个算法如何和函数的最优化联系起来呢?
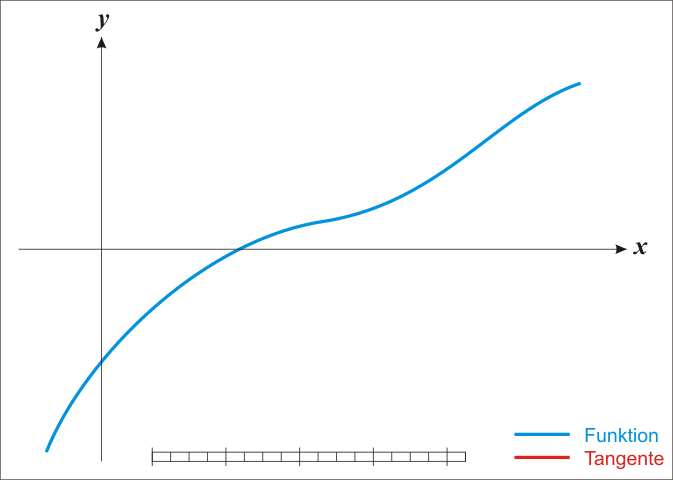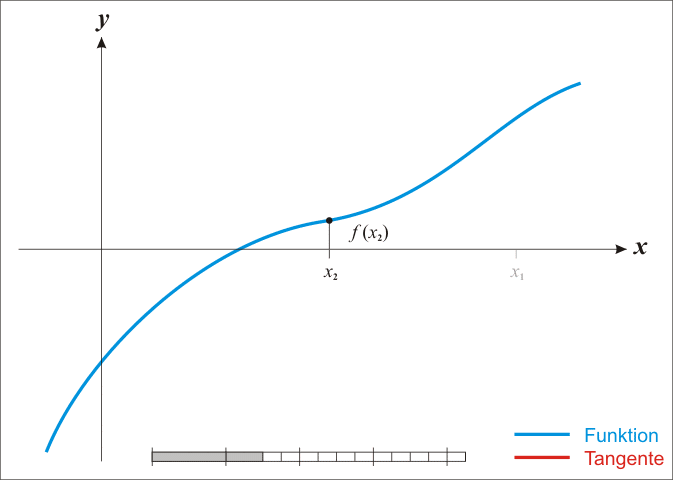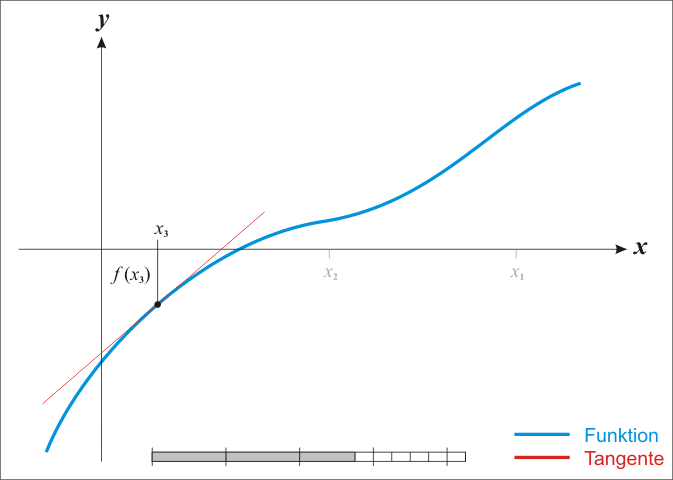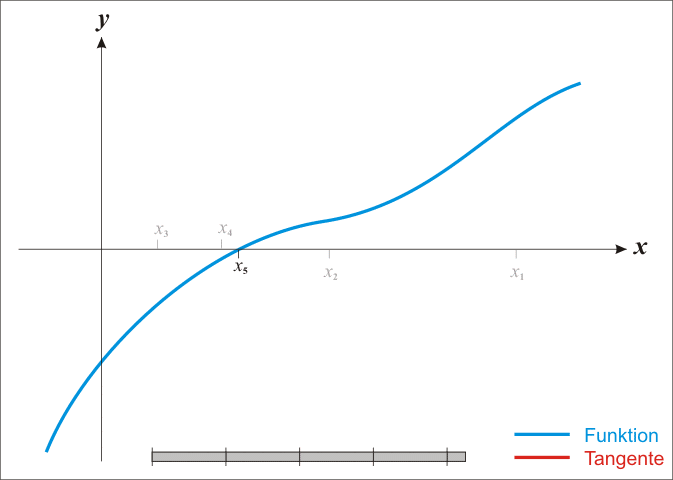
最优化
我们想要求解的问题如下:
假如 (f(x)) 是凸函数,那么我们只需要找到一阶导数为 (0) 的点,就可以得到局部最小值。因此,牛顿法在最优化问题中干的事情就是求解一阶导数的零点。接下来,类比方程求根的牛顿法,我们先将函数的一阶导数在 (x_k) 处展开。
这里 (g_k) 表示在 (x_k) 的梯度,(H_k) 表示海塞矩阵,它是向量 ( abla f(x)) 对向量 (x) 求导得出来的。
接下来令 ( abla f(x) = 0),我们可以求解出 (x)。
接下来迭代求解 (x),然后带入梯度公式去计算,如果小于 (epsilon),我们可以认为它的梯度已经够"平"了,可以停止迭代了。
拟牛顿法
思路分析
拟牛顿法主要是为了解决牛顿法中海塞矩阵求逆的问题,我们可以考虑用另外的矩阵来代替海塞矩阵。这样的一个矩阵需要满足两个条件:一,正定。二,拟牛顿条件。
拟牛顿条件是海塞矩阵需要满足的条件,如果考虑别的矩阵来替代,我们要求这样的矩阵也满足这样的条件。
将 (x=x_{k+1}) 带入下面公式,我们可以得到拟牛顿条件。
令 (y_k = g_{k+1} - g_k), (delta_{k} = x_{k+1} - x_k),代入上述式子得到:
考虑使用正定的矩阵 (G_k) 代替海塞矩阵的逆,那么我们能否保证替代之后函数值得到下降呢?
后面为了进行泰勒展开,所以这里在 (x) 的迭代公式中加入了步长 (lambda)。
在 (lambda) 足够小的情况下,可以进行在 (x) 处进行泰勒展开。
由于 (G_k) 是正定矩阵,所以 (g_{k}^{T} G_k g_k > 0)。因此在 (lambda) 足够小的情况下,(f(x)) 的函数值会在下降。使用 (B_k) 代替 (G_k) 的分析是一样的,只不过第一步要对 (B_k) 先求个逆。正定矩阵的逆也是正定的,后面的分析是一样的了。
DFP 算法
拟牛顿条件:(H_{k}^{-1} \, y_k = delta_{k})
DFP 算法使用 (G_k) 代替海塞矩阵的逆。它通过构造两个待定矩阵来迭代求解 (G_k)。构造矩阵如下:
令 (G_k \, y = -Q_k \, y) 和 (P_k \, y = delta_{k}),代入上式,可以证明下一个 (G_{k+1}) 也是满足拟牛顿条件的。
(P_k) 和 (Q_k) 的解由构造得到。(一开始我在想着两边同乘的思路呢...)
最后得到迭代公式:
在李航的书里,算法还有一步是搜索 (lambda),算法的整体步骤类似牛顿法。
BFGS 算法
拟牛顿条件:(y_k = H_{k} \, delta_{k})
我们可以使用 (G_k) 代替海塞矩阵的逆,亦可以使用矩阵 (B_k) 代替海塞矩阵。整个构造的思路类似 BFP,首先构造如下迭代公式:
接下来两边同乘 (delta_{k}):
同样令 (B_k \, delta_{k} = -Q_k \, delta_{k}) 和 (y_k = P_k \, delta_{k})。
同样可以构造出 (P_k) 和 (Q_k)
最后得到迭代公式:
总结
一句话总结:将牛顿法用于求解凸函数的一阶导数的零点,这个零点就是局部最优点。