问题来源
这个问题是在阅读一篇论文 [1] 的时候想到的。
[1] 讲的是知识图谱的正确率评估。我们将知识图谱的正确率定义为知识图谱中三元组表述正确的百分比。为了得到正确的比例,我们可以逐一判断是否正确,计算比例。可是这样需要的时间太多了,这就好比“统计一百万个人中身高大于1米8的人数”这样的问题。
对于这种调查对象非常多的情况,一般使用抽样调查。[1] 中使用的方法是,使用中心极限定理,对正确率做一个区间估计。
中心极限定理
中心极限定理讲的是,样本均值的分布趋于正态分布。
我们从知识图谱中抽样,我们得到 n 个样本:(X_1, X_2, ..., X_n, X_i = 0, 1)。
样本均值和样本方差为:(E(X_i) = mu, D(X_i) = sigma^2)
根据中心极限定理,我们有:
区间估计
改写正态分布为标准型:
使用概率形式表示置信区间:
因此我们可以说平均值 (1-alpha) 的置信区间是:
问题来了
问题是,我们并不知道总体方差是多少。我们想要求解的是总体的均值,即正确率。然而,我们既不知道总体均值,也不知道总体方差。论文中,为什么能够用未知的总体方差去求解置信区间呢?
答案
大数定律告诉我们,样本越多,估计量接近真实值,也就是说样本方差越接近真实方差。
对于大样本来说,样本方差和总体方差接近,所以我们可以使用样本方差直接替代总体方差。此外,只有样本量充分大(>30个),中心极限定理才能成立。在论文中,后面的公式都是用样本方差来替代总体方差的。
真正的问题
这里还原一下,我一开始思考的思路,因为这个思路,陷入了乱七八糟的思考。
一开始,我认为,需要抽样 n 次,每次抽样 m 个,产生 n 个随机均值,这 n 个随机均值服从正态分布。接着,我看到浙大概率论(文末有截图)中,有一个总体为正态分布的区间估计。于是,我将这 n 个随机均值套入到图中的公式。此时,还是不知道样本方差,于是我认为应该采用 t 分布才对。于是才有了题目“在方差未知的情况下,均值的区间估计问题”。总的思路是:应用中心极限定理,再应用正态总体的区间估计。但是我仍然困惑,为什么能使用正态分布,而不是 t 分布。
经过搜索,我得出如下结论:
在方差未知的情况下,均值的区间估计,根据样本量的多少,决定使用正态分布还是 t 分布。这里的样本量对应的是 n 个均值变量的多少。
- 样本量较大(>30),可以使用正态分布来做区间估计,并且直接用样本方差来代替总体方差。
- 样本量较小,使用 t 分布来做区间估计。
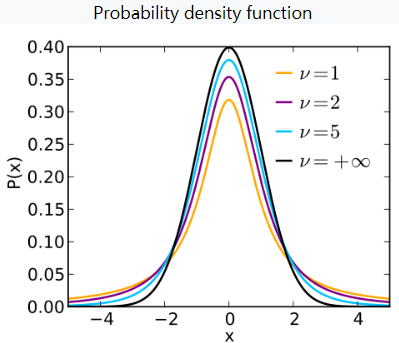
具体的原因是,t 分布随着自由度的增长,会不断趋近正态分布。t 分布的自由度为 样本容量-1。
真正的答案
其实,不需要抽样 n 次,每次抽样 m 个,这个思路我觉得没问题,但是麻烦。
我之所以产生这个思路,是因为对置信区间理解不够透彻。置信区间是,目标变量在随机区间的概率。
因此,当我们对一次采样应用中心极限定理之后,我们可以得到样本均值服从正态分布。将这个正态分布写成概率形式,于是我们可以求解置信区间了,而不是像一开始的想法那样先抽样 n 次,每次抽样 m 个。
总体流程
计算知识图谱的正确率,我们需要采样 n 个三元组。
采样 n 次产生的变量为: (X_1, X_2, ... X_n),这 n 个随机变量的均值分布服从正态分布。
我们可以得到置信区间,其中总体方差可以用样本方差来替代,n 为样本容量
参考文献
[1] Efficient Knowledge Graph Accuracy Evaluation
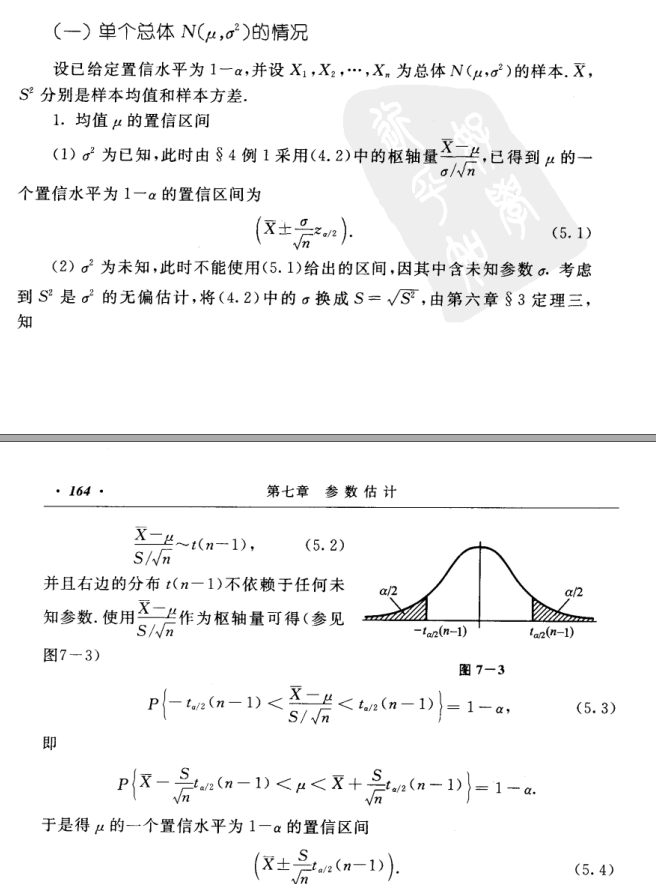
截图
来自浙大版概率论