Easy and Hard Problems:
NP完全理论是为了在可处理的问题和不可处理的问题之间画一条线,目前最重要的问题是是否这两者是本质不同的,而这个问题目前还没有被解决。典型的结果是一些陈述,比如“如果问题B有一个多项式时间的算法,那么C也会有一个多项式时间的算法”,或者逆否表述为“如果C没有多项式时间的算法,那么B也没有”。第二个表述是说,对于一些问题C以及一个新的问题B,我们先去找是否有这种关系,如果有的话我们可能不想去做问题B,先来看看C。为了描述这些东西,需要不少形式主义的记号,我们在这里尽可能地少涉及。
先来看什么是问题?一个抽象的做决定问题是从问题实例集合I到{0,1}的映射,其中0代表错误,1代表正确。为了更严谨,我们把问题实例写成I到{0,1}*,也就是0/1组成的字符串,一个具体的做决定问题是从比特串到{0,1}的映射,我们把那些没有意义的问题映射到0。举个例子来说,对于最短路径问题,一个问题事实例是一个图以及两个顶点,做决定的问题是是否存在这两个顶点之间长度至多为k的一条路径。要注意的是,做决定问题不会比相应的最优算法要复杂,也就是说其复杂度小于等于最优算法,因此为了去证明相应的最优化算法是hard的,如果我们可以证明做决定问题是hard的,那么就可以达成我们的目标。(相当于充分性)
接着来看什么是多项式时间,一个算法解决一个具体的decision问题Q时,如果对于每一个长度为n的比特串x,都可以在多项式时间内得出Q(x),那么称这个问题是多项式时间-可解的。我们的第一类问题就是P = 多项式时间可解的问题集合。P中的问题是简单的,可处理的;不在P中的问题是不可处理的,困难的。那些只需要多项式时间的算法是高效的,需要更多时间的是不高效的。一个lanuage L 是{0,1}*的子集,我们可以认为其中的元素是Q(x) = 1的,一个算法A把x映射到{0,1},A会接受那些Q(x) = 1的实例,拒绝Q(x) = 0的实例。不过language中被算法A接受的是那些Q(x) = 1的,要注意的是,在接受和决定之间有些微不同,后者包括接受和拒绝两个方面。

以哈密顿回路为一个例子,我们目前有证据表明L = {G|G有哈密顿回路}这个language应该不是P中的,但是要检验一条路径是不是哈密顿回路则可以在多项式时间内完成。所以L‘ = {(G,y) | y是G的一条哈密顿回路}是在P中的。
接着介绍一个非确定性多项式时间,更普遍地说,比起提出一个解,验证一个解更加简单,简而言之,这便是所谓NP-completeness涉及的东西。换句话说,是否接受和验证之间的不同点可以用来把复杂的问题分解成简单的问题。 NP = { L包含于{0,1}* | L被一个多项式时间算法所验证}。更加正式的说是,如果L在NP里的,那么对L里面的所有语言x以及一个待验证的y使得A(x,y)=1,其中A是一个在多项式时间内跑出来结果的算法。举个例子是,判断一个图是不是哈密顿图是NP问题,NP是non-deterministic polynomial time的缩写,非确定的计算机可以猜一个待验证的结果然后验证,但是这样的结果有很多(指数级别)。
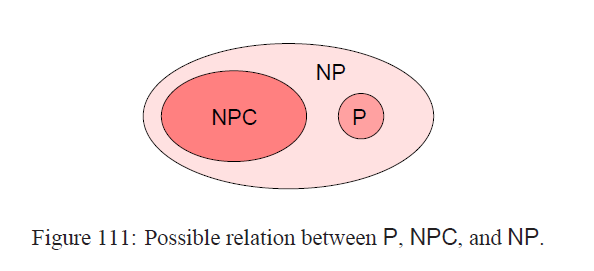
非确定机器至少和确定机器一样强大,因为每一个P中的问题都是NP中的,也就是P包含于NP,再定义co-NP问题的形式为{L|L的补命题是NP的},比如问题A“验证一个图是哈密顿图”是简单的(P问题),但是它的补B”一个图不是哈密顿图“
就看上去很麻烦,也就是说B的补是一个NP问题,那么B是一个co-NP问题。我们不难发现如果L是P问题的话,那么L的补问题也是P问题,L自然也就在co-NP中,所以P包含于co-NP,我们可以得到P,NP,co-NP之间的关系只可能有四种(见下图):
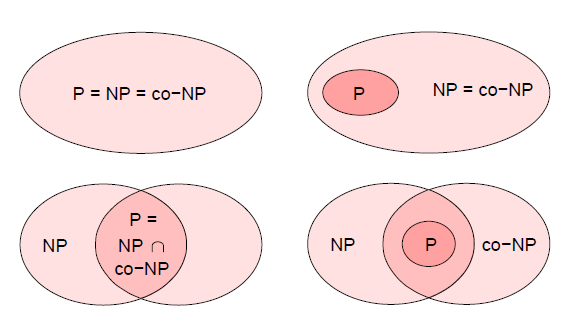
接下来介绍问题划归的概念,这是创建NP完全问题类的关键方法。想法是把第一个问题A的实例划归到B,然后把B的答案划归到A,对于判断性问题,解是一样的,而且不需要转化。如果说语言系统L1可以在多项式时间内转换到语言系统L2,那么我们记作L1 <= PL2,也就是说存在一个多项式时间内计算的函数f,把L1里面的实例一一映射到L2中的实例,现在假设L2存在一个多项式算法A我们就可以把两个算法合起来A。f,这样以来我们就得到了L1中的多项式算法,换句话说,我们得到一个划归定理,如果L1<= PL2,而且L2是一个P问题,那么L1也是一个P问题。现在定义NP-complete,一个语言系统是NP-complete的如果满足下面条件,(1)L是NP问题,(2)对每一个NP问题,都可以在多项式时间内转化到L。(2)说明L可能的确是个难问题,对于那些满足(2)但是不满足(1)的问题我们称为NP-hard问题,对于满足(1)(2)的问题全体构成了NPC问题。一个比较经典的NPC问题是逻辑满足问题,见下图:

具体的证明分两步,证明NP+所有的NP可以多项式时间内划归到它。有时间我去看看。
NP-Complete Problems:
在这一节里面,我们讨论一系列的NP完全问题,为了创造出关于困难的问题长得如何的想法。对于这类问题,去找一个多项式时间的算法看似时futile(徒劳的),我们打算进行回避并且近似地解决这类问题。一个逻辑式子,首先由若干括号组成,括号之间用且连接,括号内用或连接,一个括号里由3个命题,称这样地式子在3-CNF(conjunctive normal form)中,有结果表明判定一个3-CNF的满足性比一般的SAT问题不会简单。定义3-SAT = {x ∈ SAT | x in 3-CNF}。
首先有一个定理是SAT<=p 3-SAT。我们可以在3步内把一个命题公式转换成3-SAT满足的形式。第一步把这个命题公式写成二叉树的形式,内部节点上为符号,叶子是原子公式。以下面这个为例子:

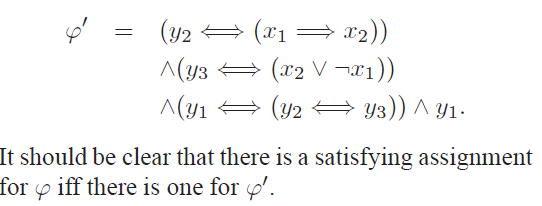
我们把原来的公式变成上面的带一撇的公式,不难发现第一个括号(y2双箭头(x1右箭头x2))的真值表如下:

由于四个式子中定会有成立的,所以我们可以用一个3-CNF中的式子来代替:
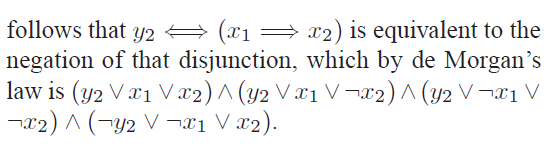
对那些小于三个原子命题的我们用下面的扩充方法:
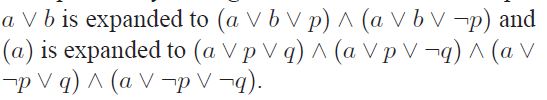
这样一来,我们就可以把SAT里面的任何一个元素转换到一个3-CNF中的元素,而且不难发现这样的转化是在多项式时间内完成的。事实上,对于3个原子命题的形式足够困难了,但是2个原子命题公式的形式(2-CNF)存在多项式算法。不难发现如果L1是NP-hard的,且可以在多项式时间内转换到NP问题L2,那么L2是NPC问题,这样我们就可以证明3-SAT是NPC问题。由于NPC问题的存在,通常认为P不等于NP,我们可以猜测P,NP,NPC的可能关系如下图:
我们可以证明最大团问题和最大独立集问题都是NPC问题,其中G的最大独立集就是G的补图的最大团,我们只要证明一个最大团问题是NPC就可以了,最大团问题的描述一般是,给定一个G={V,E}以及一个整数k,最大团问题问的是是否存在一个顶点数大于等于k的团。不难证明最大团问题是NP的,然后我们可以把3-SAT问题在多项式时间内转化到最大团,假设一个命题x有k个从句,我们创建一个图,使得每一个从句由三个顶点构成,两个顶点之间连一条边当且仅当他们不在同一个从句里面而且不互为否命题。如果说存在一个真的赋值,那么每个从句中至少都有正确的命题,也就是说,构造的图中(因为否命题不连接)至少存在一个k个顶点连接而成的团;同样的也可以反过来说,由此我们在多项式时间内完成了转换。
其他各种各样的NPC问题:k色染色问题,图的带宽问题(建立点到整数的双射,求相邻点差值的最小值),旅行商问题(完全图内找一个权重和小于等于k的圈),旅行商2(把权重映射到{1,2}),旅行商3(换成欧几里得距离)。
Approximation Algorithms:
很多问题是NP-hard的,忽视他们不是一个好方法。实际上我们可以做的事情有很多,对于小规模的问题,我们用指数级的算法都是高效的,而那些特殊化的困难问题可能存在多项式算法,我们考虑第三个选项——在多项式时间内用算法计算一个近似的解,比如说我们要最大化(或者最小化)一个cost,我们设一个a(n)-多项式算法,其中a(n)>=1(等号当且仅当产生最优解),如果实际的cost是C1,那么我们要保证我们的算法产生的C>=C1/a(n)【或者对于最小化cost的例子来说要使得C<=C1 * a(n)】。理想情况下a(n)为常数,但是有时候甚至多项式近似算法都没有。
第一个集合是点覆盖问题,也就说找出找出最小的一个顶点的集合,使得所有的边都被覆盖住,(每条边至少一个顶点在我们选出的集合里面),不难发现顶点集合V的子集V'为点覆盖集合当且仅当V-V'是一个独立集,然而后者我们在前面已经证明了寻找最大独立集是一个NPC问题,所以最小点覆盖也是NPC的。
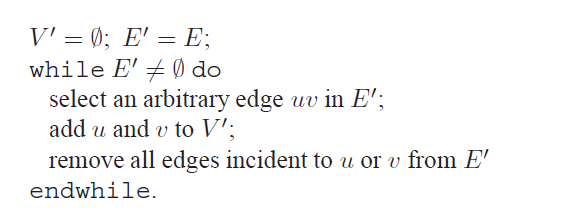
这是一个最小点覆盖的近似算法,我们可以得到a(n) = 2,也就是有C <= 2C1,实际上我们求得是一个匹配,对于二部图,有多项式算法来计算这个东西。
第二个问题是旅行商问题。一次旅行路径A是一条哈密顿回路,我们要使得cost(A)最小,我们先假设所有的代价都满足三角不等式,即w(uv) <= w(uw) + w(wv),(实际上即使有了一个条件还是NPC的),我们可以cost(A)至少是最小生成树的代价,使用prim算法需要O(n^2)的时间,而cost(A)不会超过两倍的MST代价,实际上我们可以把两倍的MST看成每条边来回两次,这样可以保证回到原处(根据三角不等式得到严格证明)。此处的常数是在三角不等式的条件下得到,否则我们可以构造下面这个反例,使得找到常数C是NP-HARD的:

第三个问题是集合覆盖问题,设F是一个集族,X是集合,如果F的广义并是X,我们的问题是找出F的最小子集A,使得A的广义并是X。下main是一个贪心方法,每一步选择一个集合,使得这个集合和没有被选择的交集最大:

最后我们来分析一下时间消耗,设Hd = 1+1/2 +...+1/d(调和级数前d项和),不难发现Hd <= 1 + lnd for d >= 1,令m为集族F中元素的元素个数最大值。我们断言,这个贪心算法有一个Hm的近似。证明如下:

Homework:
选几个把:



