欧拉函数Euler(x)
Euler(n)表示1-n之间与n互质的个数,例如Euler(4) = 2,其中1和3与4互质。(数论里面规定Euler(1) = 1,并且1与任何数互质)。
欧拉函数的通项表达式为:
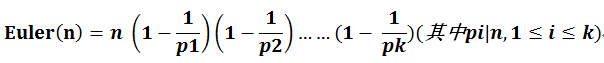
还有其一些推论:

当n >= 1时,1 - n中与n互质的整数和为nEuler(n)/2;
那欧拉函数怎么求呢?
首先我们再来学习下一个概念:积性函数。
函数f(x)对于任意正整数a, b,如果a,b互质并且满足f(ab) = f(a)f(b),则f(x)为积性函数。其中若a,b不互质仍满足f(ab) = f(a)f(b)则称f(x)为完全积性函数。

对于一个数n和他的约数p:

对于任意一个正整数n, 均有:
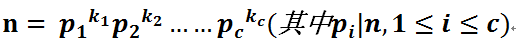
再根据积性函数的性质得:
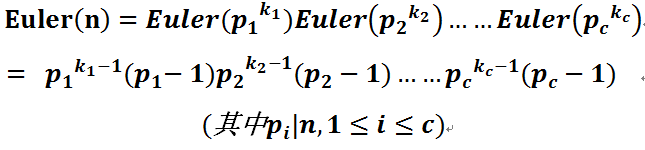
也就是先预处理使Euler[i] = i,再去考虑能被n的质因数,只要把其中一个质因数p改成p - 1即可。
附上伪代码:
const int N = 1000000 + 5;
int euler[N];
void euler_function(){
for(int i = 0; i <= N - 5; i ++) euler[i] = i;
for(int i = 2; i <= N - 5; i ++)
if(euler[i] == i)
for(int j = 1; i * j <= N - 5; j ++)
euler[i * j] = euler[i * j] / i * (i - 1);
}
当然,上述算法(类似于埃式筛法)的复杂度为(n + nloglogn)。
然后我们再想想筛选素数的方法除了埃式筛法,还有更快速的线筛(素数筛选传送门)


附上代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000000 + 5;
int n;
int check[N], euler[N], prime[N];
void euler_function(){
memset(check, 0, sizeof(check));
euler[1] = 1;
int tot = 0;
for(int i = 2; i <= N - 5; i ++){
if(!check[i]){
prime[tot ++] = i;
euler[i] = i - 1;
}
for(int j = 0; j < tot; j ++){
if(i * prime[j] > N - 5) break;
check[i * prime[j]] = 1;
if(i % prime[j] == 0){
euler[i * prime[j]] = euler[i] * prime[j];
break;
}
else euler[i * prime[j]] = euler[i] * (prime[j] - 1);
}
}
}
int main(){
euler_function();
while(scanf("%d", &n) == 1)printf("%d
", euler[n]);
return 0;
}