http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1963
题意：
有m个坑，每只兔子会在ti时刻回到坑中，现在有n个人，每个人都可以从任意时间（<0也可以）从第一个坑出发，速度为1，如果路过的坑中有兔子，就给它喂食物，每只兔子喂一次即可，计算所有兔子等待时间的最短之和。
思路：
对于第i只兔子，如果有个人在y时间正好经过喂了它，那么那个人出发的时间为y-x。现在现计算出每只兔子的y-x值，记为t【】，并排好序。sum【】表示前i只兔子的y-x值。
接下来就是动态转移了，d【i】【j】表示第i个人正好经过第j只兔子时的最小等待时间。
那么状态转移方程就是
d[i][j]=min(d[i][j],d[i-1][k]+(j-k)*t[j]-(sum[j]-sum[k]))
解释一下这个方程的意思：d【i-1】【k】表示上一个人正好经过第k只兔子时的最小等待时间，那么j~k之间的兔子肯定是要轮到第i个人来喂了，因为第i个人的出发时间更晚一些，所以j~k这些兔子肯定是要等待的，等待的时间就是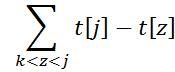
，也就是上式的(j-k)*t[j]-(sum[j]-sum[k])。
理解了这个之后，接下来就是斜率优化dp的应用了，这样的状态转移方程也容易让人想到斜率优化dp。
设z<k<j，如果k的决策比z的决策更好，那么在上述的状态转移方程中满足
d[i-1][k]+(j-k)*t[j]-(sum[j]-sum[k]) < d[i-1][z]+(j-z)*t[j]-(sum[j]-sum[z])
整理得到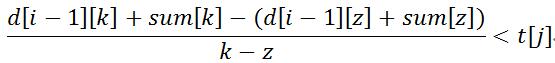
，那这就是明显的斜率优化dp了。
所谓的斜率优化dp，就是每新插入一个点的时候，需要维护一条下凸的形状，对于会形成上凸的点，我们可以直接删去，因为它肯定不会是最优解。
那么如何维护呢？使用单调队列。
每次依次先检查队首的两个元素，如果满足上式，那么说明队首的第二个值更优，可以删除第一个值，直到第一个值比第二个元素更优。
然后是队尾的检查，如果新插入的点使得队尾的点成为了上凸点，那么就需要删去这个上凸点，直到没有上凸点产生。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<sstream> 6 #include<vector> 7 #include<stack> 8 #include<queue> 9 #include<cmath> 10 #include<map> 11 #include<set> 12 using namespace std; 13 typedef long long ll; 14 typedef pair<int,int> pll; 15 const int INF = 0x3f3f3f3f; 16 const int maxn = 1e5+ 5; 17 18 int n, m, p; 19 ll t[maxn]; 20 ll Q[maxn]; 21 ll sum[maxn]; 22 ll dis[maxn]; 23 ll d[105][maxn]; 24 25 ll dy(int i, int j, int k) 26 { 27 return (d[i-1][j]+sum[j])-(d[i-1][k]+sum[k]); 28 } 29 30 ll dx(int j, int k) 31 { 32 return j-k; 33 } 34 35 int main() 36 { 37 //freopen("in.txt","r",stdin); 38 while(~scanf("%d%d%d",&n, &m, &p)) 39 { 40 dis[1]=0; 41 for(int i=2;i<=n;i++) 42 { 43 scanf("%I64d",&dis[i]); 44 dis[i]+=dis[i-1]; 45 } 46 47 for(int i=1;i<=m;i++) 48 { 49 int x,y; 50 scanf("%d%d",&x,&y); 51 t[i]=y-dis[x]; 52 } 53 54 sort(t+1,t+m+1); 55 sum[0]=0; 56 for(int i=1;i<=m;i++) 57 sum[i]=sum[i-1]+t[i]; 58 59 for(int i=1;i<m;i++) 60 d[1][i]=t[i]*i-sum[i]; 61 62 63 for(int i=2;i<=p;i++) 64 { 65 int frt=0, rear=-1; 66 for(int j=1;j<=m;j++) 67 { 68 while(frt<rear && dy(i,Q[frt+1],Q[frt])<t[j]*dx(Q[frt+1],Q[frt])) frt++; 69 while(frt<rear && (dy(i,Q[rear],Q[rear-1])*dx(j,Q[rear]))>=(dy(i,j,Q[rear])*dx(Q[rear],Q[rear-1]))) 70 rear--; 71 Q[++rear]=j; 72 73 int tmp=Q[frt]; 74 d[i][j]=d[i-1][tmp]-(tmp-j)*t[j]-(sum[j]-sum[tmp]); 75 } 76 } 77 cout<<d[p][m]<<endl; 78 } 79 return 0; 80 }