3 逻辑回归

逻辑回归

逻辑回归
感谢

逻辑回归是用来解决分类问题的

分类问题

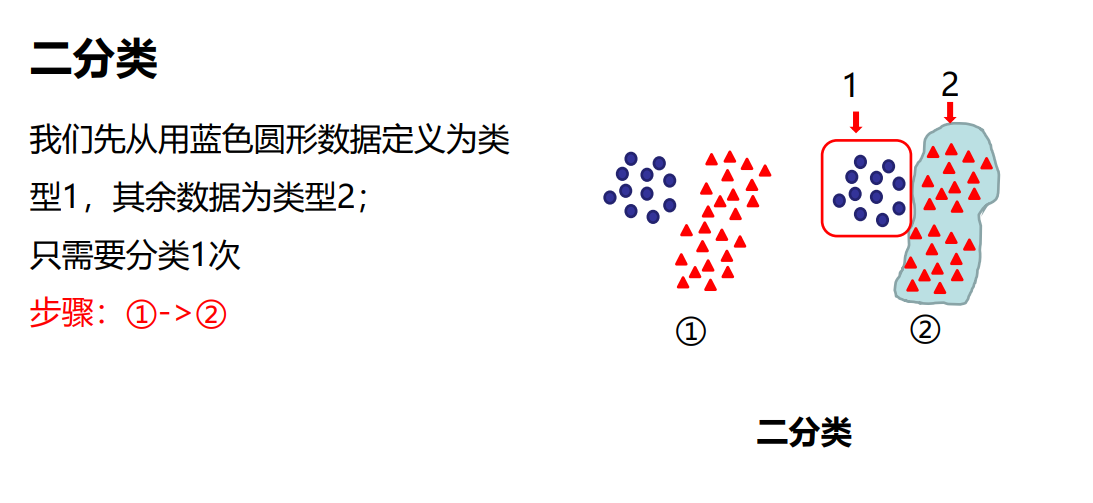
二分类就是将两类物体分开

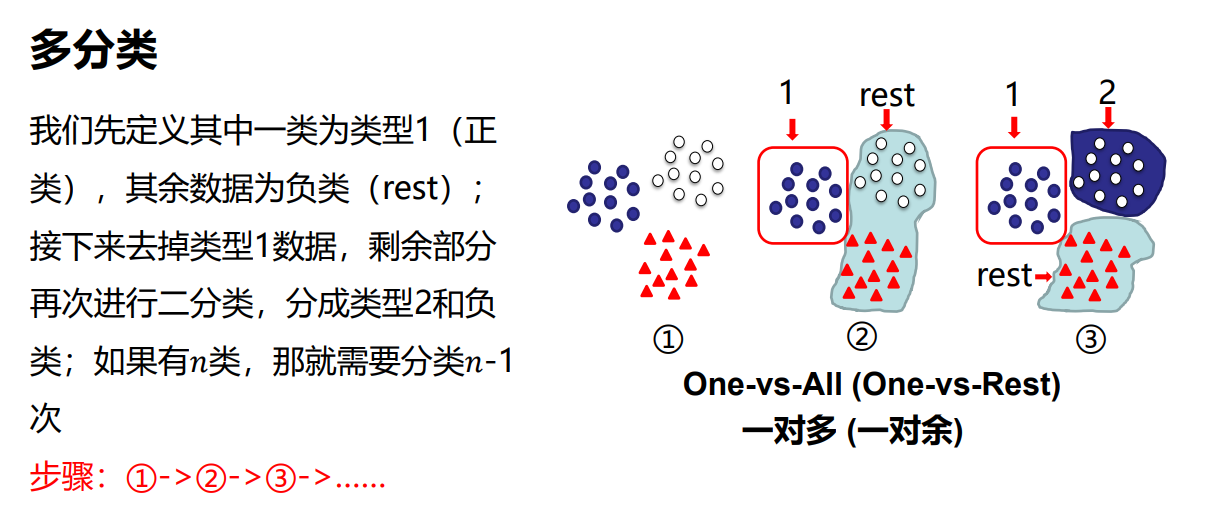
多分类每次只分类出一类物体，有n个物体，则需要做n-1次二分类

sigmoid 函数

选择sigmoid函数的原因

线性回归的函数 ℎ = = ，范围是(−∞, +∞)。而分类预测结果需要得到[0,1]的概率值。

回归：输出的是连续数据，目的是找到最优的拟合。（例如：预测气温）
分类：输出的是离散数据，目的是找到决策边界。（例如：预测硬币正反）

我们其实想要的是一个单位阶跃函数，通过一个分类面来将样本分为两类。

\[\epsilon(t)=\left\{ \begin{aligned} &0 \ & t<0 \\ &1 \ & t>0 \\ \end{aligned} \right. \]

图像为

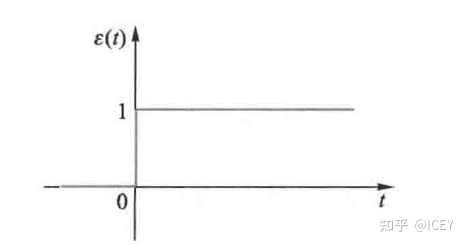
jieyue

由于单位阶跃函数不连续，我们希望找到一个平滑相似的函数来代替，我们选择使用sigmoid函数来代替

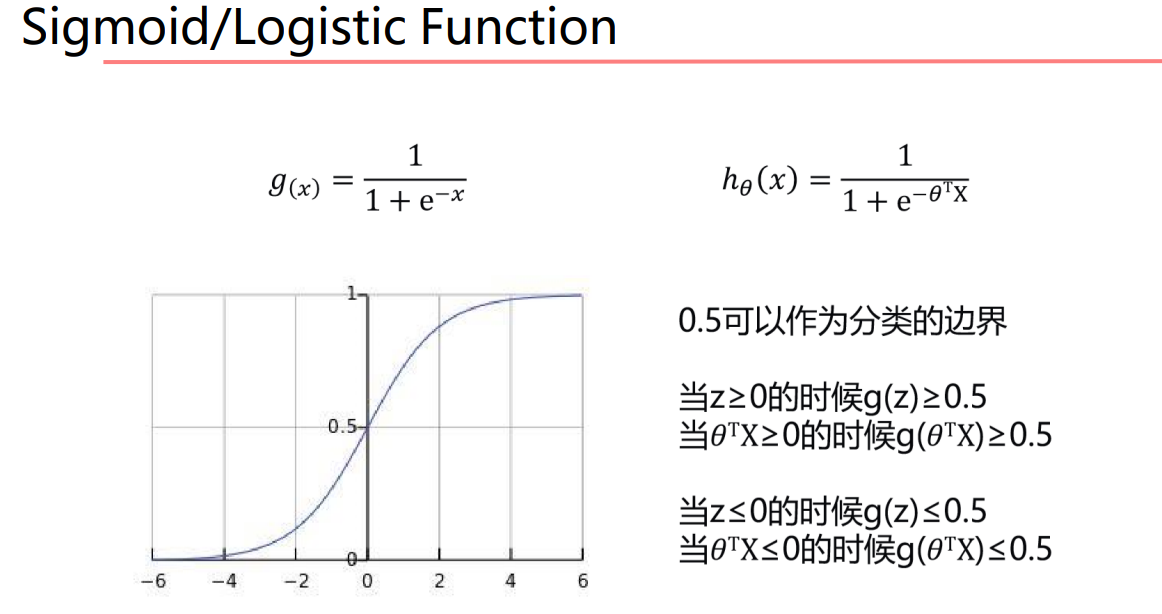
这时，x为样本，g(x)就是样本被分类得到的值，这时候 0.5 就可以作为分类面，将所有样本很好地分开。

同时sigmoid函数求导有很好的形式

sigmoid求导

\[\begin{aligned} g(z)=\frac{1}{1+e^{-z}} \\ g(z)'&=(\frac{1}{1+e^{-z}} )' \\ &=\frac{e^{-z}}{(1+e^{-z})^2} \\ &=\frac{1+e^{-z}-1}{(1+e^{-z})^2} \\ &=\frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})}) \\ &=g(z)(1-g(z)) \end {aligned} \]

事件发生比Odds 到Logit

事件的发生比odds：事件发生与事件不发生的概率之比为 1− ，称为事件的发生比（the odds of experiencing an event）其中为随机事件发生的概率，的范围为[0,1]。

\[Odds(A) 事件A的发生比 = \frac{事件A发生的概率}{事件A不发生的概率}= \frac{P(A)}{1-P(A)} \\ = \frac{\frac{Number \ of \ Event \ A}{Total \ Number \ of \ Events}}{\frac{Number \ of \ Other\ Event }{Total \ Number \ of \ Events}} =\frac{Number \ of \ Event \ A}{ Number \ of \ Other\ Events} \\ \]

事件发生比Odds 与概率的关系

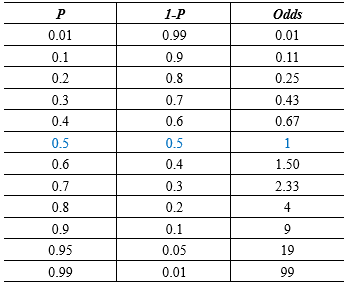
事件发生比于概率的关系

概率$P$的变化范围是$[0,1]$，而Odds的变化范围是$[0, +\infty]$

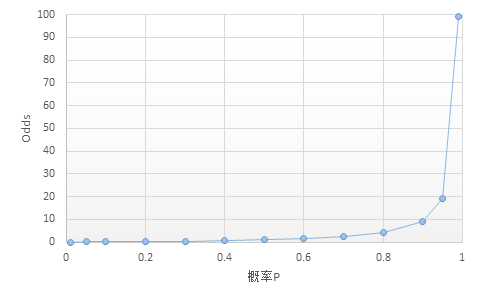
P与Odds的图像

反过来，我们有

\[P(A=1)(事件A发生的概率) = \frac{事件A的发生比}{1+事件A的发生比} \\ 验证： \\ \frac{Odds(A)}{1+Odds(A)} = \frac{\frac{P}{1-P}}{1+\frac{P}{1-P}}=\frac{\frac{P}{1-P}}{\frac{1-P+P}{1-P}} = P(A) \]

Logit

对Odds取对数就得到了 Logit

\[logit = log (Odds)=log \frac{P}{1-P} \]

Logit的一个很重要的特性就是没有上下限,或者说其变化范围是$[- \infty ,+\infty]$

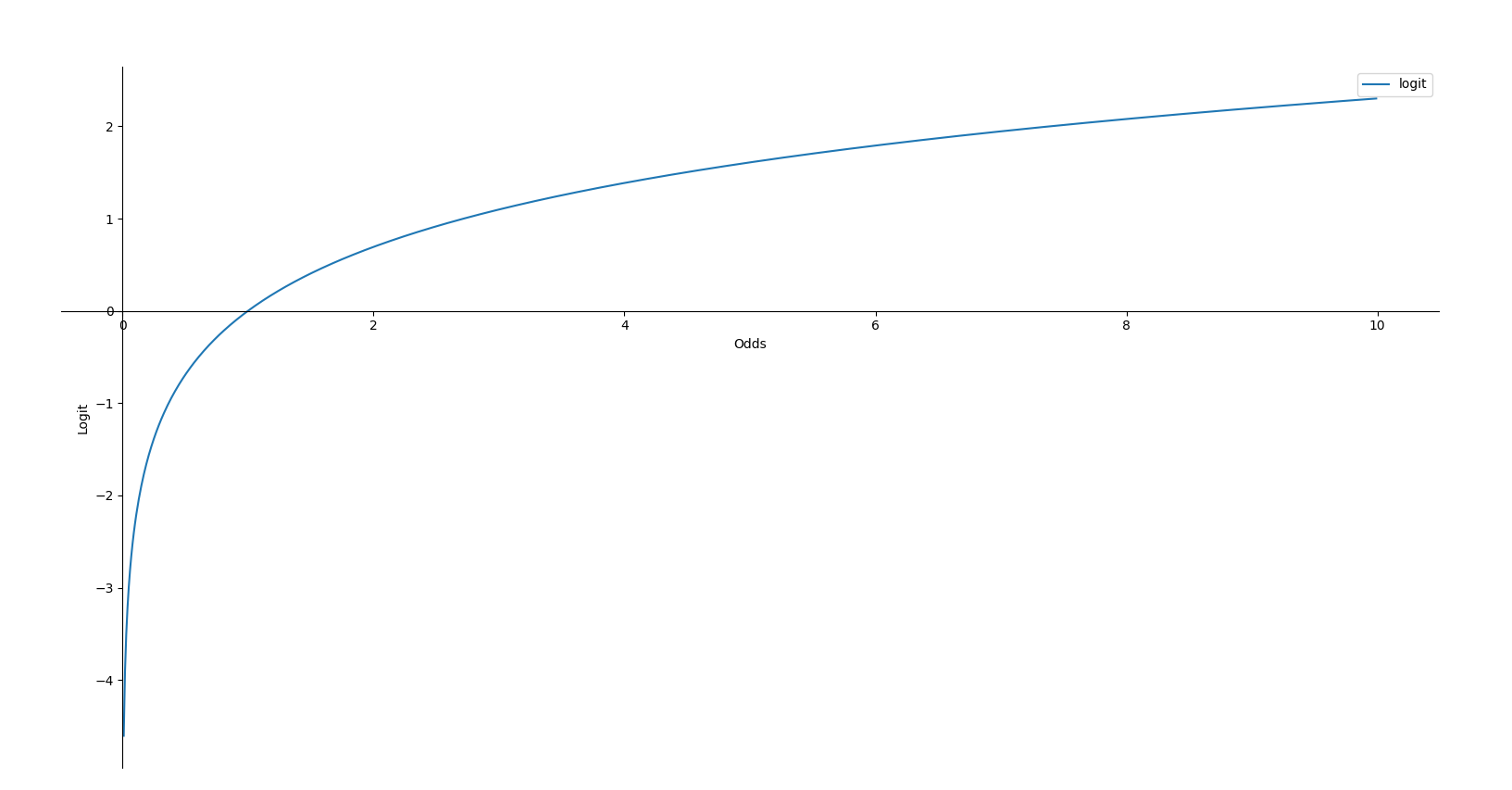
反过来，我们有

\[Odds(A) = e^{logit} = e^{log \frac{P}{1-p}} \]

通过logit函数，我们就能将概率$P$从$[0,1]$ 映射到$[- \infty ,+\infty]$

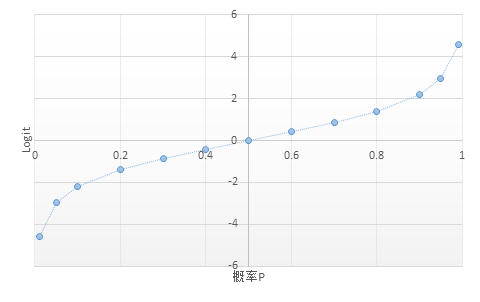
p与logit

同样，反过来，我们也可以将$[- \infty ,+\infty]$映射到概率$P[0,1]$

\[P(A=1)(事件A发生的概率) = \frac{事件A的发生比}{1+事件A的发生比} \\ =\frac{e^{logit}}{1+e^{logit}} \]

在二分类问题中，我们认为$P(y=1|x)$为把样本$x$标记为正例的可能性，$P(y=0|x)$为把样本$x$标记为反例的可能性。我们用logit函数来预测结果，即$z = logit()$

于是有

\[P(y=1|x) =\frac{e^{z}}{1+e^{z}} = \frac{e^{wx+b}}{1+e^{wx+b}} \\ P(y=0|x) =\frac{1}{1+e^{z}} = \frac{1}{1+e^{wx+b}} \]

当$z$接近于正无穷，概率值接近于1；当$z$接近于负无穷，概率值接近于0.

代价函数（损失函数）的理解

。

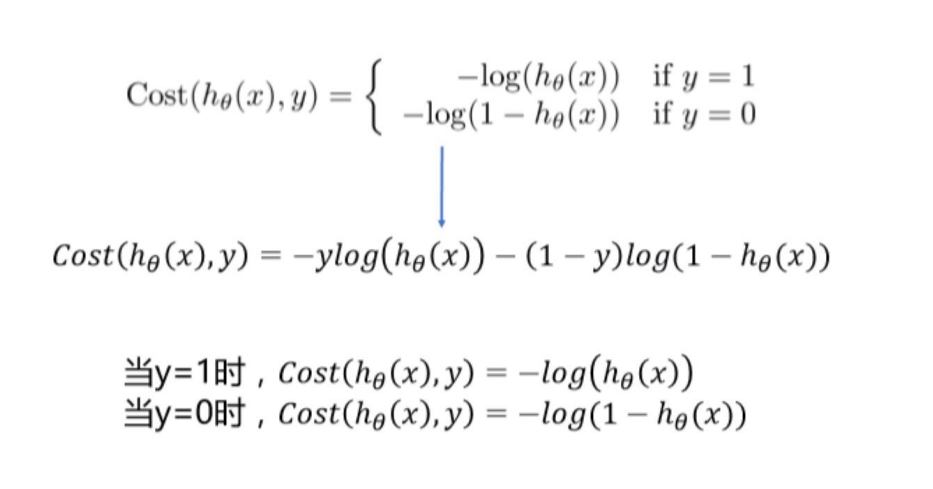
为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对个样本的损失函数求和然后除以:

\[J(w)=\frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)},y^{(i)}) \\=\frac{1}{m}[-\sum^m_iy^{(i)}logh_\theta(x^{(i)})-(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \\ =-\frac{1}{m}[\sum^m_iy^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \]

这里的$\theta$和$w$是一个含义，都是表示机器学习需要学习的参数

1 似然函数法理解

为什么使用最大似然估计而不用最小二乘法

https://www.zhihu.com/question/65350200

损失函数是人为设计的。

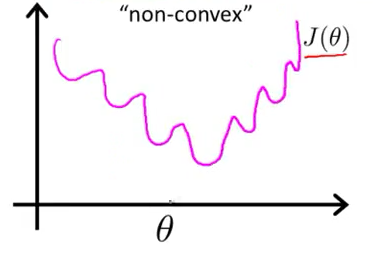
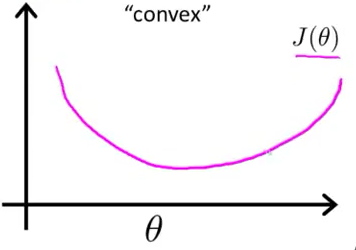
最小二乘非凸，最大似然凸。下面是图像

\[E_{w,b} = \sum_{i=1}^m(y_i-\frac{1}{1+e^{-(w^Tx_i+b)}})^2 \]

上图是最小二乘，可以看到容易陷入局部最小值。

\[L_{w,b}=\sum_{i=1}^m(-y_i(w^Tx_i+b)+ln(1+e^{w^Tx_i+_b})) \]
是关于$(w,b)$的高阶连续可导凸函数

我们用逻辑回归来作为分类模型，将$p = \frac{1}{1+e^{-\theta^Tx}} =\frac{1}{1+e^{-z}}$ 看做逻辑回归中样本的概率。

因为是分类问题，我们假设其服从二项分布，我们使用最大似然函数来估计参数$w$ 。

因为假设服从二项分布，于是我们有

\[P(Y=1 |x) = h(x) ; P(Y=0|x)=1-h(x) \]

我们可以使用极大似然估计来估计参数$\theta$，似然函数为

\[max L(\theta) = \prod^m_{i=1} P(y^{(i)}|x^{(i)};\theta) =\prod^m_{i=1} (h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y(i)} \]

两边取对数

\[l(\theta)=\sum_{i=1}^m (y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))) \]

代价函数为

\[J(\theta)=-\frac{1}{m}l(\theta)=- \frac{1}{m}[\sum^m_iy^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \]

我们有

\[p(y=1|x) = \frac{e^{\theta x}}{1+e^{ \theta x}} \\ p(y=0|x) = \frac{1}{1+e^{\theta x}} \]

2 交叉熵理解 ——从极大似然估计到KL散度

https://zhuanlan.zhihu.com/p/266677860

2.1 极大似然估计要解决的问题

给定一个数据分布 $P_{data(x)}$
给定一个由参数 $\theta$ 定义的数据分布 $P_G(x;\theta)$
我们希望求得参数$\theta$ 使得$P_G(x;\theta)$ 尽可能接近 $P_{data(x)}$

可以理解成：

$P_G(x;\theta)$ 是某一具体的分布（比如简单的高斯分布），而 $P_{data(x)}$是未知的（或者及其复杂，我们很难找到一个方式表示它），我们希望通过极大似然估计的方法来确定 $\theta$ ，让$P_G(x;\theta)$能够大体表达$P_{data(x)}$

从 $P_{data}$ 采样m个样本 $\{x^1,x^2,\dots,x^m\}$
计算采样样本的似然函数 $L=\Pi_{i=1}^m P_G(x^i;\theta)$
计算使得似然函数 $L$ 最大的参数 $\theta: \theta^* = arg \ \underset{\theta}{max} L=arg \ \underset{\theta}{max} \Pi_{i=1}^m P_G(x^i;\theta)$

这里再啰嗦一下极大似然估计为什么要这么做：
$P_{data}$ 可以理解成是非常复杂的分布，不可能用某个数学表达精确表示，因此我们只能通过抽象，使用一个具体的分布模型 $P_G(x;\theta)$近似 $P_{data}$
所以，求 $P_G(x;\theta)$ 的参数 $\theta$的策略就变成了：
我们认为来自 $P_{data}$的样本 $\{x^1,x^2,\dots,x^m\}$ 在 $P_G(x;\theta)$分布中出现的概率越高，也就是 $L=\Pi_{i=1}^m P_G(x^i;\theta)$越大 , $P_G(x;\theta)$和 $P_{data}$ 就越接近。
因此，我们期待的 $\theta$ 就是使得 $L=\Pi_{i=1}^m P_G(x^i;\theta) $最大的 $\theta$.
即： $ \theta^* = arg \ max_\theta L=arg \ max_\theta \Pi_{i=1}^m P_G(x^i;\theta)$

咱们继续推导：

\[\begin{aligned} \theta^* &= arg \ \underset{\theta}{max} L \\ &=arg \ \underset{\theta}{max} \Pi_{i=1}^m P_G(x^i;\theta) \\ &=arg \underset{\theta}{max} \ log \Pi_{i=1}^m P_G(x^i;\theta) \\ &=arg \underset{\theta}{max} \ \sum_{i=1}^m log P_G(x^i;\theta) \\ & \approx arg \underset{\theta}{max} E_{x \sim P_{data}} [log P_G(x;\theta)] \\ &= arg \underset{\theta}{max} \int_{x} P_{data}(x) log P_G(x;\theta) dx = H(p,q)（交叉熵）\\ &= arg \underset{\theta}{max} \int_{x} P_{data}(x) log P_G(x;\theta) dx - \int_x P_{data}(x)logP_{data}(x)dx \\ &(我们求的是\theta，后面加上的一项与\theta 无关，这是为了将极大似然的式子推导为KL散度的表达)\\ &= arg \ \underset{\theta}{min} KL(P_{data}||P_{G}(x;\theta)) \end{aligned} \]

KL散度：
$KL(P||Q)$ 衡量P，Q这两个概率分布差异的方式：
$KL(P||Q)=\int_x p(x)(log \ p(x)-log\ q(x))$

2.2 极大似然估计的本质

找到 $\theta$ 使得 $P_G(x;\theta)$ 与目标分布 $P_{data}(x)$ 的KL散度尽可能低，也就是使得两者的分布尽可能接近，实现用确定的分布 $P_G(x;\theta)$ 极大似然 $P_{data(x)}$

梯度下降求解

\[J(\theta)=- \frac{1}{m}[\sum^m_iy^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \]

\[\theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} \\ \]

\[\begin{aligned} \frac{\partial(h_\theta(x),y)}{\partial\theta_j} &= -\frac{1}{m}\sum_{i=1}^m [\frac{y^i}{h_\theta(x^{(i)})} \cdot \frac{\partial h_\theta(x^{(i)})}{\partial\theta_j}+\frac{1-y^i}{1-h_\theta(x^{(i)})} \cdot -\frac{\partial h_\theta(x^i)}{\partial\theta_j}] \\ &= -\frac{1}{m}\sum_{i=1}^m [(\frac{y}{h_\theta(x^{(i)})}-\frac{1-y}{1-h_\theta(x^{(i)})})\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j}] \\ &=-\frac{1}{m}\sum_{i=1}^m [(\frac{y-h_{\theta}(x^{(i)})}{h_{\theta}(x^{(i)})(1-h_{\theta}(x^{(i)}))} )h_\theta(x^{(i)})(1-h_\theta(x^{(i)}))x_j^{(i)}] \\ &=\frac{1}{m}\sum_{i=1}^m[(h_\theta(x^{(i)})-y)x^{(i)}_j] \end{aligned} \]

复合函数求导法则

对$ylog(h_\theta(x))$求导

\[\frac{\partial ylog(h_\theta(x))}{\partial \theta} = \frac{y}{h_\theta(x)} \cdot \frac{\partial h_\theta(x)}{\partial\theta} \]
对$(1-y)log(1-h_\theta(x))$求导

\[\frac{\partial (1-y)log(1-h_\theta(x))}{\partial \theta} = \frac{1-y}{1-h_\theta(x)} \cdot -\frac{\partial h_\theta(x)}{\partial\theta} \]
$h_\theta'(z)=h_\theta(z)(1-h_\theta(z))$

$z = \theta \cdot x$

\[\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j} =h_\theta(x^{(i)})(1-h_\theta(x^{(i)})) \frac{\partial(z^{i})}{\partial{\theta_j}} \\ = h_\theta(x^{(i)})(1-h_\theta(x^{(i)})) x_j^{(i)} \]

逻辑回归正则化

查准率/查全率/F1指标

代码实现

感谢

https://www.jianshu.com/p/b6bb6c035d8c

Logit究竟是个啥？——离散选择模型之三 - 知乎 (zhihu.com)

一文搞懂熵(Entropy),交叉熵(Cross-Entropy) - 知乎 (zhihu.com)

交叉熵(Cross Entropy) - 简书 (jianshu.com)