单变量线性回归
在这个文档中将会介绍单变量线性回归模型的建立和公式推倒,通过实例的代码实现算法来加深理解
一.模型推导
1-1 线性回归模型
设定样本描述为
[x=(x_1;x_2;...;x_d)
]
预测函数为
[f(oldsymbol x)=w_1x_1+w_2x_2+...+w_dx_d+b
]
一般向量形式
[f(oldsymbol x)=oldsymbol w^Tx+b
]
[oldsymbol w=(w_1;w_2;...;w_d)
]
1-2 单变量线性回归
最小二乘法模型
单变量线性回归中,样本的特征只有一个,所以回归模型为
[f(oldsymbol x)=wx+b ag{1}
]
为了使得模型预测的性能更好,这里使用均方误差最小化进行评估
[E_{(w,b)}= frac{1}{m} sum^m_{i=1}(f(x_i)-y_i)^2=frac{1}{m}sum^m_{i=1}(y_i-wx_i-b)^2 ag{2} \
]
为了让均方误差最小,就等价于下式
[(w^*,b^*)=minsum^m_{i=1}(f(x_i)-y_i)^2=minsum^m_{i=1}(y_i-wx_i-b)^2
]
误差分别对w和b求导,得
[egin{align}
frac{partial E_{(w,b)}}{partial w}=& 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}(y_i-b)x_i
ight) ag{3} \
frac{partial E_{(w,b)}}{partial b}=& 2left(mb - sum^m_{i=1}(y_i-wx_i)
ight) ag{4}
end{align}
]
令(3)和(4)为零,联立解方程,详细步骤如下
[left{
egin{array}{}
frac{partial E_{(w,b)}}{partial w}=0 \
frac{partial E_{(w,b)}}{partial b}=0
end{array}
ight.
]
- 先令(4)为零,解得
[b=frac{1}{m}sum^m_{i=1}(y_i-wx_i) ag{5}
]
- 再将(5)式代入(3)得
[egin{align}
frac{partial E_{(w,b)}}{partial w}
&= 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}(y_i-b)x_i
ight) \
&= 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}left(y_i-frac{1}{m}sum^m_{i=1}(y_i-wx_i)
ight)x_i
ight) \
&= 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}left(y_i-frac{1}{m}sum^m_{i=1}y_i + frac{w}{m}sum^m_{i=1}x_i
ight)x_i
ight) \
&= 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}left(y_i-frac{1}{m}sum^m_{i=1}y_i
ight)x_i - frac{w}{m}sum^m_{i=1}(sum^m_{i=1}x_i)x_i
ight) \
&= 2left(wsum^m_{i=1}x_i^2 - sum^m_{i=1}left(x_i-frac{1}{m}sum^m_{i=1}x_i
ight)y_i - frac{w}{m}(sum^m_{i=1}x_i)^2
ight) \
&= 2left(w left(sum^m_{i=1}x_i^2 - frac{1}{m}(sum^m_{i=1}x_i)^2
ight) - sum^m_{i=1}left(x_i-frac{1}{m}sum^m_{i=1}x_i
ight)y_i
ight) = 0 \
end{align}
]
[w =frac{sum^m_{i=1}left(x_i-frac{1}{m}sum^m_{i=1}x_i
ight)y_i} {sum^m_{i=1}x_i^2 - frac{1}{m}(sum^m_{i=1}x_i)^2} = frac{sum^m_{i=1}y_ileft(x_i- overline{x}
ight)} {sum^m_{i=1}x_i^2 - frac{1}{m}(sum^m_{i=1}x_i)^2} ag{6}
]
因此得到最后的公式(5)和(6),即可求解出单变量线性回归模型的参数。
#### 梯度下降法
在吴恩达的机器学习课程中,有说明:在特征值的数量低于1万的时候,使用正规方程比较合适。大于1万的时候,使用梯度下降比较合适。 在后面的机器学习中,更多的还是使用梯度下降算法。
(梯度下降相关内容,后续补上)
二、实例代码
例题1
假设存在已知的输入数据
X = [x1, x2, ... , x10] = [1, 2, 4, 5, 6, 7, 8, 9, 10]
已知的输出的数据
y = [20.52, 27.53, 29.84, 36.92, 38.11, 37.21, 40.96, 46.37, 49.78, 50.22]
求解以下问题
- 利用最小二乘法求解出线性模型 y = wx +b 中的参数w和b,并计算出训练均方误差E
- 在得到最小二乘模型的基础上,若模型输入新数据x'=[11, 12, 13],请计算出模型的预测值y'
- 若模型输入新数据x'=[11, 12, 13],实际测量值y=[52.38, 55,66, 58.31]
代码:Matlab
x = [1 2 3 4 5 6 7 8 9 10];
y = [20.52 27.53 29.84 36.92 38.11 37.21 40.96 46.37 49.78 50.22];
%% 根据上面的公式(5)(6)计算w和b
w = sum(y.*(x-mean(x)))/(sum(x.^2)-1/10*(sum(x))^2);
b = 1/10*sum(y-w*x);
%% 绘制图形
plot(x,y,'o');hold on
plot(x,w*x+b);hold on
legend('native', 'predict', 'Location', 'NorthWest')
%% 根据公式(2)计算训练误差
Et = sum((w*x+b-y).^2)/10
%% 输入新的数据,进行预测
x_ = [11 12 13];
y_ = w*x_+b
ym = [52.38 55.66 58.31];
figure;
plot(x_,y_,'r-.',x_,ym,'b');hold on
legend('predict', 'native')
Ep = sum((y_-ym).^2)/3
运行结果

实际数据和预测数据
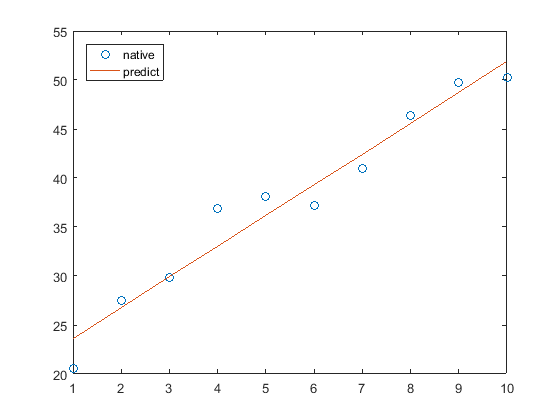
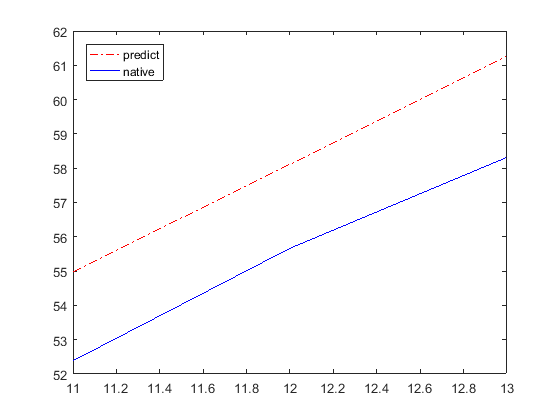
输入新的数据和预测值
### 代码:Python
这里再次强调一下上面的公式,可以更好结合代码
[egin{align}
w&=frac{sum^m_{i=1}y_ileft(x_i- overline{x}
ight)} {sum^m_{i=1}x_i^2 - frac{1}{m}(sum^m_{i=1}x_i)^2} \
b&=frac{1}{m}sum^m_{i=1}(y_i-wx_i)
end{align}
]
import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
y = np.array([20.52, 27.53, 29.84, 36.92, 38.11, 37.21, 40.96, 46.37, 49.78, 50.22])
def fit(x, y):
w = 0.0
b = 0.0
if(len(x) != len(y) or len(x) == 0):
print('input data is error!')
return w,b
w = np.sum(y*(x - np.mean(x)))/(np.sum(x*x) - (1/len(x))*pow(np.sum(x), 2))
b = (1/len(x))*np.sum(y - w*x)
return w,b
w, b = fit(x, y)
print('w :', w)
print('b :', b)
y_ = w*x +b
x_new = np.array([11, 12, 13])
y_new = np.array([52.38, 55.66, 58.31])
y_new_ = w*x_new + b
# 误差
E = np.sum(pow((y - y_), 2))/len(x)
E_new = np.sum(pow((y_new - y_new_), 2))/len(x_new)
print('E :',E)
print('E_:',E_new)
# 绘图
plt.subplot(121)
plt.scatter(x, y, label='native')
plt.plot(x, y_, 'red', label='predict')
plt.legend(loc='best')
plt.subplot(122)
plt.plot(x_new, y_new, label='native')
plt.plot(x_new, y_new_, '-.', color = 'r', label='predict')
plt.legend(loc='best')
plt.show()
运行结果
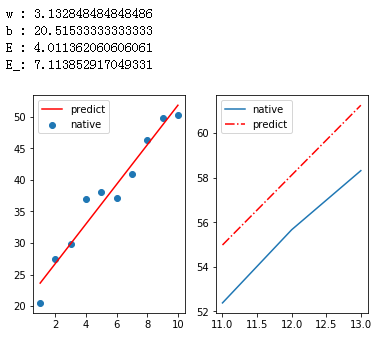
三、总结
- 主要介绍了单变量线性回归的原理,公式推倒和代码实现
- 为了对比验证结果是否正常,采用的两种编程语言,后面更多的会使用Python
- 后续继续整理多变量线性回归