转载链接
https://blog.csdn.net/Nothing_but_Fight/article/details/98721177
https://blog.csdn.net/weixin_44751481/article/details/98587703
看完这两篇应该就能搞懂辽~
这个题目感觉挺难想的,用到了dp,当时理解也理解了很久,所以想着把它给记录下来
Problem Description
You are given three positive integers N,x,y.
Please calculate how many permutations of 1∼N satisfies the following conditions (We denote the i-th number of a permutation by pi):
p1=x
pN=y
for all 1≤i<N, |pi−pi+1|≤2
Input
The first line contains one integer T denoting the number of tests.
For each test, there is one line containing three integers N,x,y.
1≤T≤5000
2≤N≤105
1≤x<y≤N
Output
For each test, output one integer in a single line indicating the answer modulo 998244353.
Sample Input
3
4 1 4
4 2 4
100000 514 51144
Sample Output
2
1
253604680
核心思想:
对于任何一个n的全排列,都要恰好用到1~n这n个数字一次。
题意问n的所有全排列中满足的条件的全排列有几个。
我们不从所有的全排列中选择,而是用n个数构造数列,看看能构造出多少个数列。
在从左向右构造的过程中,数列有两个极值要达到(也就是1和n),
根据两个极值在数列中的位置,我们将全排列分成五类:
1、x=1且y=n,两个极值一个起始位置(最左侧),另一个在末位置(最右侧)。(题目保证x<y,也就是1在最左侧,n在最右侧)。
2、x!=1且y!=n,两个极值都不在排列的始末位置。(一般情况)
3、x=1且y!=n,1在最左侧,n不在最右侧。
4、x!=1且y=n,1不在最左侧,n在最右侧。
5、y-x=1。
第一类:
第一类排列的数量可以用动态规划得到:
定义dp[i]:i的全排列中,首项是1,末项是i,并且相邻两项的绝对差值不超过2的数列的个数。
首项是1,第二项有两种情况:
1、直接填2,数量是dp[i-1]
2、填3,那么第三项只能填2(因为如果填其他值,2就再也填不上了),第四项只能填4。数量是dp[i-3]
状态转移方程:
dp[i]=dp[i-1]+dp[i-3]
第二类:
由于数列相邻两项的绝对差值不超过2,我们往返极值的路径是唯一确定的。(往返的路径一奇一偶,从x去极小值1时路径的奇偶性与x一致,从极大值n返回y时路径的奇偶性与y一致),详见下图:
这样我们就将样例的第三个
100000 514 51144
转化成了
50629 1 50629
转换公式就是:N,x,y <==> y-x-1,1,y-x-1
这样第二类就成了第一类了,输出dp[y-x-1]即可。
第三类:
第二类有两个极值需要到达,而第三类1已经在最左侧了,需要到达极大值n(上图右边的路径是唯一确定的),也就是1~y-1是可变的,输出dp[y-1]即可。
第四类:
与第三类如出一辙,第四类n已经在最右侧了,需要到达极小值1(上图左边的路径是唯一确定的),也就是x+1~n是可变的,输出dp[n-x]。
第五类:
这一类是特殊情况,不用上述的dp。
相邻两项的绝对差值不超过2,路径的宽度只够往返一次的,如下图所示:
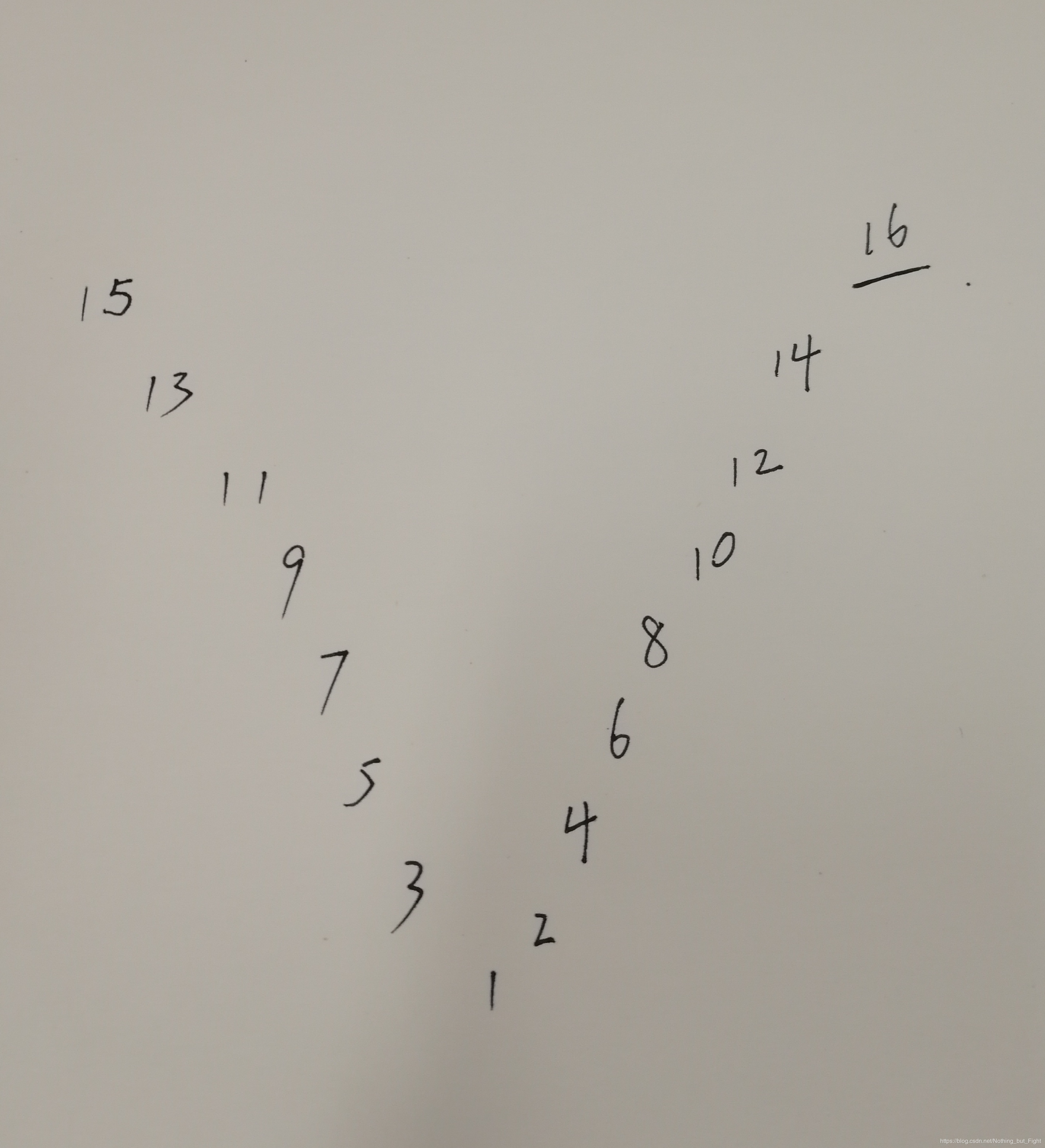
在这里插入图片描述此时,分情况讨论:
1、如果x=1或y=n(一个极值在始末位置,另一个极值在中间),往返一次极值就够了,且整个路径是唯一确定的(去时奇偶性与x一致,返回时路径奇偶性与y一致),输出1即可。
2、其他情况,需要往返两次极值,但是路径宽度只够往返一次的,构造不出数列,输出0即可。