( exttt{Solution})
首先考虑 ( exttt{dp}) 维护题目要求的深度为 (i), 每个节点最多经过一次的不同有向路径数量 (f_i)。
明显的,只维护这个东西是不对的,因为忽视了这样的情况:
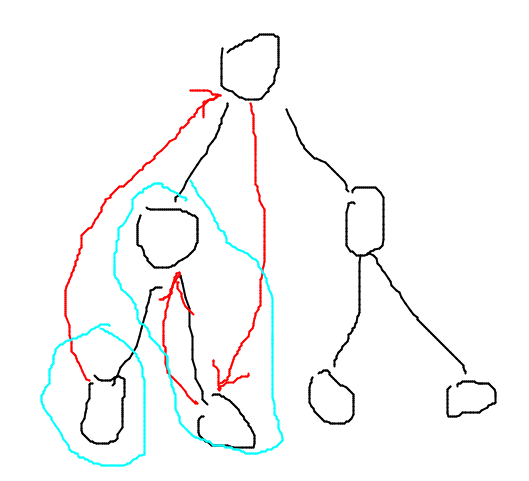
这样子这条路径是由原来的被蓝色圈圈包住的两个部分转移而来。
那么考虑记录 (g_i) 为两条不相交的有向路径数量。
然后蒟蒻兴冲冲地去 尝试了, 并过了前两个样例,但是过不了第三个样例,这是为什么?
发现 (g_i) 也有可能是由三条不相交的有向路径转移而来!
那么正解就浮出水面了:维护深度为 (i), (j) 条不相交的有向路径数量 (dp_{i,j})。
转移如果想明白了状态其实很简单。这里还是说一下。
首先用背包求出深度为 (i-1), 和为 (j) 条不相交的有向路径数量 : bb[j] += dp[i - 1][k] * dp[i - 1][j - k]
第一种转移:根结点独立,然后其他的路径让两个子树自由组合 : dp[i][j] += bb[j - 1] + 2 * dp[i - 1][j - 1]
第二种转移:路径不包括根结点,或根结点为路径起点或终点: dp[i][j] += (2 * j + 1) * bb[j] + (4 * j + 2) * dp[i - 1][j]
第三种转移:路径包括根结点,且连接两条原来在子树中是两条链: dp[i][j] += j * (j + 1) * bb[j + 1] + 2 * j * (j + 1) * dp[i - 1][j + 1]
( exttt{Code})
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j; i <= k; i++)
#define R(i, j, k) for(int i = j; i >= k; i--)
using namespace std;
const int N = 444;
const int mod = 1e9 + 7;
int n, dp[N][N], bb[N];
int main() {
scanf("%d", &n);
dp[1][1] = 1;
L(i, 2, n) {
fill(bb, bb + n + 1, 0);
L(j, 1, n) L(k, 0, j) (bb[j] += 1ll * dp[i - 1][k] * dp[i - 1][j - k] % mod) %= mod;
dp[i][1] = 1;
L(j, 1, n) {
int t = 0;
(dp[i][j] += (2ll * j + 1) * bb[j] % mod) %= mod;
(dp[i][j] += (4ll * j + 2) % mod * dp[i - 1][j] % mod) %= mod;
(dp[i][j] += 1ll * j * (j + 1) % mod * bb[j + 1] % mod) %= mod;
(dp[i][j] += 2ll * j * (j + 1) % mod * dp[i - 1][j + 1] % mod) %= mod;
(dp[i][j] += bb[j - 1] % mod) %= mod;
(dp[i][j] += 2ll * dp[i - 1][j - 1] % mod) %= mod;
}
}
printf("%d
", dp[n][1]);
return 0;
}