
要求二项式的幂的某个系数的话,到了初中就应该会知道可以用 杨辉三角 这个东西来求系数。举几个例子吧:
1 1 2 1 1 3 1 2 1 (a+b)^2=a^2+2ab+b^2 4 1 3 3 1 (a+b)^3=a^3+3ba^2+3ab^2+b^3 5 1 4 6 4 1 …… 6 1 5 10 10 5 1 ……
根据这两个例子就能看出:杨辉三角的第 n 行对应的就是 (a+b)的 n-1 次方的各项系数。再看杨辉三角的规律:每一项都是这一项岁对应的上面两个数的和,所以我们可以打印杨辉三角,在做些运算就可以A掉这个题啦。
先说怎么求杨辉三角,一般都是定义一个二维数组,假设为 a[][];根据杨辉三角的规律,可以得到一个递推式:
a[i][j]=a[i-1][j-1]+a[i-1][j];
不要忘了先将 a[1][1]赋值为 1
代码:
1 a[1][1]=1; 2 for(int i=2;i<=k+1;++i) // k是(a+b)的次数 3 { 4 for(int j=1;j<=k+1;++j) 5 { 6 a[i][j]=a[i-1][j-1]+a[i-1][j]; 7 } 8 }
注意:i 要从2开始循环,因为 a[1][1]已经赋值了,如 i 从1开始的话,a[1][1]会被重新赋值为0,这样打印出来就都是0;
虽然这种打印杨辉三角的方法没有任何问题,但是看数据范围:
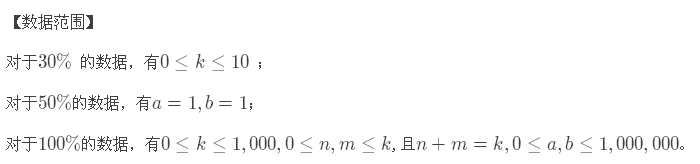
k≤10000,这样的话就数组就至少要开 a[10000][10000];而且仅是 int 类型的话这个二维数组所占内存为: 10000×10000×4÷1024÷1024≈381.47MB;
将近是内存限制的3倍,这肯定不行,所以就有了另一种内存占用比较少的方法:既然我们只需要杨辉三角的第 k+1 行,所以我们可以定义一个一维数组来存储 k=1时的数,推出 k=2时的数后,再将这个一维数组更新,这样不断更新来减少内存;
代码:
1 a[1]=1; // 依旧要赋值为1 2 b[1]=1; // 同上 3 for(int i=2;i<=k+1;++i) // i代表 当(a+b)为 i 次方时 4 { 5 for(int j=2;j<=i+1;++j) // 当(a+b)为 i 次方时,展开后一共会有 i+1 项,因为第一项的系数始终为1,所以数组从 2 到 i+1 更新 6 { 7 a[j]=b[j-1]+b[j]; // 递推式 8 } 9 for(int j=2;j<=i+1;++j) // 将本次循环所更新后的数储存,以便下一次的递推 10 { 11 b[j]=a[j]; // 进行赋值 12 } 13 }
定义了两个数组,a[10010] 和 b[10010],a来存储当前的数值,b来存储上一次的数值,用来递推。所以最终a数组存储的就是(a+b)^k的每项系数。
(a+b)^k的系数求出来后,不要忘了题目中要求求的是(by+ax)^k展开后 x^n*y^m项的系数。这个系数其实就是b^m*a^n*a[m+1]或者是b^m*a^n*a[n+1];
完整代码:
1 #include<iostream> 2 using namespace std; 3 long long a[10010]; 4 long long b[10010]; 5 const long long mod=10007;// 要求对10007取余 6 int main() 7 { 8 a[1]=1; 9 b[1]=1; 10 long long a2,b2,a1,b1,k,n,m; 11 cin>>a1>>b1>>k>>n>>m; 12 if(n==0 && m==0) // 特判 13 { 14 cout<<"0"; 15 return 0; 16 } 17 a1%=mod,b1%=mod; 18 a2=a1,b2=b1; 19 for(int i=2;i<=k+1;++i) 20 { 21 for(int j=2;j<=i+1;++j) 22 { 23 a[j]=(b[j-1]+b[j])%mod; // 分步取模,防止炸long long 24 a[j]%=mod; 25 } 26 for(int j=2;j<=i+1;++j) 27 { 28 b[j]=a[j]%mod; 29 } 30 } 31 for(int i=2;i<=n;++i) 32 { 33 a1*=a2; 34 a1%=mod; 35 } 36 for(int i=2;i<=m;++i) 37 { 38 b1*=b2; 39 b1%=mod; 40 } 41 long long ans=((a[m+1]*a1)%mod*b1)%mod; 42 cout<<ans; 43 return 0; 44 }