权值线段树
权值线段树 和 普通线段树 别无二致,只不过 普通线段树非叶节点维护 ([a_l, a_r]) 的信息,其每个非叶节点维护的是值为 ([l,r]) 的信息。如果不理解的话,可以看看下面用 权值线段树 维护 (a) 数组每个数出现的个数 的例子(当然我们得假设已知 (1 leq a_i leq 8) 才行):

我们可以看出,用常规方法建的权值线段树的空间复杂度为 (O(Alog A)) (其中 (A) 为 (max a_i), 下同)。一旦值域范围稍微大一些,如常见的到 (a_i leqslant 10^9) 的话,那么就会空间超限。
线段树动态开点
为了解决上面的问题,我们发现:对于一颗如上的用常规方法的权值线段树(尤其是值域大的),里面会有很多完全没有维护任何信息的节点(毕竟你想放满一个 (a_i leqslant 10^9) 的权值线段树的话 (n) 也要到 (10^9) ),如果我们不在一开始建树的时候,就浪费空间建它那不就完事了?就是啊!
动态开点线段树,顾名思义是一种可以随时建立一个点的线段树。一开始线段树是空的,当我们有用到一个节点的需要的时候(比如新增了某一个元素),才开这个点。

分析一下 动态开点的权值线段树 的空间复杂度:因为对于新增的每一个点,我们最多增加 (log A) 个节点,所以空间复杂度最坏是 (n log A) 的(并且通常卡不满)。
实现
int ls[maxn], rs[maxn], val[maxn], cnt, rt;
//ls:左儿子, rs:右儿子, val:维护的权值, cnt:当前点的个数, rt:树根
void update(int &x, int l, int r, int pos, int k){
if(!x) x = ++cnt;
if(l == r){
/*do something*/
return;
}
int mid = (l+r) >> 1;
if(pos <= mid) update(ls[x], l, mid, pos, val);
else update(rs[x], mid+1, r, pos, val);
pushup(x);
}
int main(){
//...
update(rt, 1, n, some_pos, some_val);
//...
}
看起来,除了第一句 x = ++cnt 和一个怪异的 rt与cnt 以外,好像没有什么不同的。其实动态开点的线段树也没啥特殊,特点就在第一句的 x = ++cnt上。
这句话的意思是:如果当前的 x 代表的点(指传的参)不存在(if(!x)),就给他分配一个位置 (x = ++cnt),以后就由这个 x 来代表 ([l,r]) 这个区间了。结合图片,应该可以理解。
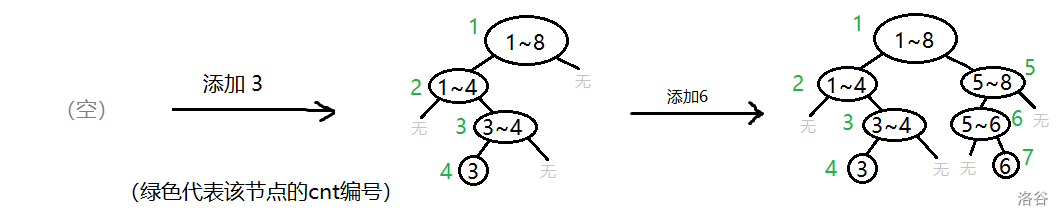
那么新建的节点怎么成为上一个节点的儿子,并且建造自己的子节点的呢?由于 x 是传的一个地址,改了 x 原来传的参也会改,通过 update(ls[x], ...) 就能给 ls[x] 赋值,就可以给新建的节点新建属于它自己的儿子了。
那个 rt 又是怎么回事呢? 完全可以直接把 rt 当成 (1) 就可以了啊?在这个例子里,确实。这个先按着不表,后面会讲到。
线段树合并
假如我们有两个 根节点维护的区间都是一样的 动态开点线段树,那么我们就可以用下面的方法合并两个树成一个新的树:
在一棵完全的(就是开满了节点的线段树)递归 :
- 如果这一个节点,两棵树上都没有,那么新的树上也不会有,就直接
return; - 如果这一个节点,只有一颗树上有,那么新的树上的节点就等同原来的那一个,直接返回存在的那一个的编号;
- 如果这一个节点,两棵树上都有,那么合并这两个树上这个节点维护的信息,继续递归到左右儿子。
我们又假设每个点维护的是 在 ([l,r]) 内的数的个数,那么我们看一个例子:

- 由于 ([5,8]) 只在左边的树上有,所以新树直接用了
cnt = 5的那个节点作为右儿子; - 由于 ([3,4]) 两边的树上都有,所以就沿用其中一个树的节点(两个树都可以,这里用的是左边的);
- 由于 ([1,2]) 两个数都没有,所以新树也没有;
- 对于每一个节点,它的权值都是两个树上的那个点的权值相加(空点权值为0)。
那么说到这里,刚才的 rt 的含义也就解决了:由于实际用上线段树合并的时候通常都会有 (10^4) 以上个动态开点线段树,又不可能给每个线段树都开尽可能大的空间 (不然空间就炸了),所以我们必然只能用同一些数组,来表示所有不同的树的 左儿子、右儿子、权值等信息。所以我们需要一种方法来找到不同的树。而 rt 数组就是方法:我们记录每一个线段树的树根的 cnt,这样子要查每一棵树就直接从 rt 开始往下查即可。
考虑合并的时间复杂度:明显,复杂度瓶颈在两个树都有同一个节点的情况,这个时候需要遍历两边树上的每一个节点,同时还要合并信息,所以复杂度为 (O(两个树的相同点数 imes 合并信息的时间复杂度))
实现
比较好理解,按照上面的模拟就可以了
//两个树merge了以后x1代表的树会变成结果,两个树上都有一个节点的时候默认用x1的那颗树的。
int merge(int x1, int x2, int l, int r){
if((!x1) || (!x2)) return x1+x2;//如果这个节点两棵树都没有(x1 = 0 && x2 = 0) 返回的就是0(没有这个节点);
//如果这个节点有一边有(x1 != 0 && x2 = 0,反之亦然),那么return 的就是那个节点的编号
if(l == r){
//合并信息...
return x1;
}
int mid = (l+r)>>1;
ls[x1] = merge(ls[x1], ls[x2], l, mid);
rs[x1] = merge(rs[x1], rs[x2], mid+1, r);
pushup(x1);
return x1;
}
例题
基本上所有用上权值线段树的题,都要用动态开点,都要线段树合并,而且大多都是用权值线段树维护状态信息。/kk
CF600E Lomsat Gelral
题面
给定一棵 (n) 个点的树,根为 (1),第 (i) 个点颜色编号为 (c_i)。对于每个点,问在它子树内出现次数达到最大值(可能有多种颜色达到最大值,都算做最大值)的颜色编号之和。 (1leq c_i≤n≤10^5)。
解法
这种题,就是我前面提到的用权值线段树维护状态信息的题。
我们可以给原题的树上每一个点,都开一个动态开点的权值线段树。每个节点的线段树,用来维护以这个节点为根的子树的 每种颜色的出现次数的最大值。
初始时,每个树节点的线段树都是空。然后,每一个节点都把自己所有儿子的线段树合并起来,再加上自己这个树节点的颜色信息,就可以得到维护以这个节点为根的子树的 每种颜色的出现次数的最大值 的线段树了。
关于数组上界:可以算出每个树的 要新建的节点的期望个数在 (log n) 个左右。所以总数组开个 (20) 倍的 maxn 就够了。
#include <iostream>
#include <cstdio>
#include <cstring>
namespace ztd{
using namespace std;
typedef long long ll;
template<typename T> inline T read(T& t) {//fast read
t=0;short f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-f;ch=getchar();}
while (ch>='0'&&ch<='9') t=t*10+ch-'0',ch=getchar();
t*=f; return t;
}
}
using namespace ztd;
const int maxn = 2e5+7;
int n, a[maxn];
struct edge{int y, gg;}e[maxn<<1];
int last[maxn], ecnt;
inline void addedge(int x, int y){
e[++ecnt] = (edge){y, last[x]};
last[x] = ecnt;
}
int rt[maxn], ls[maxn*20], rs[maxn*20], num[maxn*20], cnt; ll ans[maxn*20], ANS[maxn*20];
inline void pushup(int x){ //常规的线段树上传
if(num[ls[x]] < num[rs[x]]){
num[x] = num[rs[x]];
ans[x] = ans[rs[x]];
}else if(num[ls[x]] > num[rs[x]]){
num[x] = num[ls[x]];
ans[x] = ans[ls[x]];
}else if(num[ls[x]] == num[rs[x]]){
num[x] = num[rs[x]];
ans[x] = ans[rs[x]] + ans[ls[x]];
}
}
void update(int &x, int l, int r, int pos, int val = 1){
if(!x) x = ++cnt;
if(l == r){
ans[x] = l;
num[x] += val;
return;
}
int mid = (l+r)>>1;
if(pos <= mid) update(ls[x], l, mid, pos, val);
else update(rs[x], mid+1, r, pos, val);
pushup(x);
}
int merge(int x1, int x2, int l, int r){
if((!x1) || (!x2)) return x1+x2;
if(l == r){
num[x1] += num[x2];
return x1;
}
int mid = (l+r)>>1;
ls[x1] = merge(ls[x1], ls[x2], l, mid);
rs[x1] = merge(rs[x1], rs[x2], mid+1, r);
pushup(x1);
return x1;
}
void dfs(int x, int fa){
//初始时这个子树是空的
for(int i = last[x]; i; i = e[i].gg){
int y = e[i].y;
if(y == fa) continue;
dfs(y,x);
rt[x] = merge(rt[x], rt[y], 1, n);
}
update(rt[x], 1, n, a[x]);
ANS[x] = ans[rt[x]];
}
signed main(){
read(n);
for(int i = 1; i <= n; ++i){
read(a[i]);
//一开始就把每个树的根节点都建好,省的以后还得搞
rt[i] = i; ++cnt;
}
int xx, yy;
for(int i = 1; i < n; ++i){
read(xx); read(yy);
addedge(xx,yy); addedge(yy,xx);
}
dfs(1,0);
for(int i = 1; i <= n; ++i) cout << ANS[i] << ' ';
return 0;
}
洛谷P4556【模板】线段树合并
题面
你有一棵 (n) 个节点的树,(m) 次操作。每次操作给出 (x,y, z),然后对 (x) 到 (y) 的路径上(包含 (x,y) )的所有节点打上一个 (z) 标签。求所有操作结束过后每一个节点哪一种标签最多。(1 leq n,m,z leq 10^5)。
解法
思路和上一题接近:给每一个点维护一个动态开点权值线段树。不同点在于还需要维护 LCA 然后树上差分。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
namespace ztd{
using namespace std;
typedef long long ll;
template<typename T> inline T read(T& t) {//fast read
t=0;short f=1;char ch=getchar();double d = 0.1;
while (ch<'0'||ch>'9') {if (ch=='-') f=-f;ch=getchar();}
while (ch>='0'&&ch<='9') t=t*10+ch-'0',ch=getchar();
t*=f; return t;
}
}
using namespace ztd;
const int maxn = 300005;
int n, m, s = 1;
int last[maxn], ecnt;
struct edge{int y, gg;} e[maxn<<1];
inline void addedge(int x, int y){
e[++ecnt].y = y; e[ecnt].gg = last[x];
last[x] = ecnt;
}
int tot, first[maxn], dep[maxn], id[maxn], Fa[maxn];
inline void dfs(int x, int fa, int now){
first[x] = ++tot; id[tot] = x; dep[tot] = now, Fa[x] = fa;
for(int i = last[x]; i; i = e[i].gg){
int y = e[i].y;
if(y == fa) continue;
dfs(y,x,now+1);
id[++tot] = x; dep[tot] = now;
}
}
int ST[maxn][21], Log[maxn];
inline void STpre(){
Log[0] = -1;
for(int i = 1; i <= tot; ++i) Log[i] = Log[i>>1] + 1;
for(int i = 1; i <= tot; ++i) ST[i][0] = i;
for(int j = 1; (1<<j) <= tot; ++j){
for(int i = 1; i+(1<<j)-1 <= tot; ++i){
int x = ST[i][j-1], y = ST[i+(1<<j-1)][j-1];
if(dep[x] < dep[y]) ST[i][j]=x;
else ST[i][j]=y;
}
}
}
inline int LCA(int x, int y){
if(first[x] > first[y]) swap(x,y);
int s = first[x], t = first[y];
int len = Log[t-s+1];
if(dep[ST[s][len]] < dep[ST[t-(1<<len)+1][len]]) return id[ST[s][len]];
else return id[ST[t-(1<<len)+1][len]];
}
int X[maxn], Y[maxn], W[maxn];
int rt[maxn<<5], ls[maxn<<5], rs[maxn<<5], num[maxn<<5], cnt; ll ans[maxn<<5], ANS[maxn<<5];
inline void pushup(int x){
if(num[ls[x]] < num[rs[x]]){
num[x] = num[rs[x]];
ans[x] = ans[rs[x]];
}else if(num[ls[x]] >= num[rs[x]]){
num[x] = num[ls[x]];
ans[x] = ans[ls[x]];
}
}
void update(int &x, int l, int r, int pos, int val){
if(!x) x = ++cnt;
if(l == r){
ans[x] = l;
num[x] += val;
return;
}
int mid = (l+r)>>1;
if(pos <= mid) update(ls[x], l, mid, pos, val);
else update(rs[x], mid+1, r, pos, val);
pushup(x);
}
int merge(int x1, int x2, int l, int r){
if((!x1) || (!x2)) return x1+x2;
if(l == r){
num[x1] += num[x2];
ans[x1] = l;
return x1;
}
int mid = (l+r)>>1;
ls[x1] = merge(ls[x1], ls[x2], l, mid);
rs[x1] = merge(rs[x1], rs[x2], mid+1, r);
pushup(x1);
return x1;
}
void dfs(int x, int fa){
for(int i = last[x]; i; i = e[i].gg){
int y = e[i].y;
if(y == fa) continue;
dfs(y,x);
rt[x] = merge(rt[x], rt[y], 1, 1e5);
}
if(num[rt[x]]) ANS[x] = ans[rt[x]];
else ANS[x] = 0;
}
signed main(){
read(n); read(m);
for(int i = 1, xx, yy; i < n; ++i){
read(xx); read(yy);
addedge(xx,yy); addedge(yy,xx);
}
dfs(s,-1,0);
STpre();
for(int i = 1; i <= m; ++i){
read(X[i]); read(Y[i]); read(W[i]);
}
for(int i = 1; i <= m; ++i){
int x = X[i], y = Y[i];
int lca = LCA(x, y);
update(rt[x], 1, 1e5, W[i], 1);
update(rt[y], 1, 1e5, W[i], 1);
update(rt[lca], 1, 1e5, W[i], -1);
update(rt[Fa[lca]], 1, 1e5, W[i], -1);
}
dfs(1, -1);
for(int i = 1; i <= n; ++i) cout << ANS[i] << '
';
return 0;
}
洛谷P3224 【HNOI2012】永无乡
题面
有 (n) 个点,每个点有一个独一无二的权值 (p_i),初始时有的点已经连了边。有 (q) 次操作,有两种操作:
- 操作 1 :给 (x,y) 两点连边
- 操作 2 :询问与点 (x) 联通的所有的点中,权值第 (y) 小的点的编号。
(1 leq n, q,p_i leq 10^5)
解法
首先须要维护一个并查集来维护连通性。然后对于每一个点维护一个权值线段树,维护自己的并查集子树上的点的权值情况。然后每次询问的时候先找到自己所在并查集的根,然后对根询问区间第 (k) 小就行了。
#include <iostream>
#include <cstdio>
#define lson t[x].l
#define rson t[x].r
#define mid ((l+r)>>1)
using namespace std;
const int maxn = 1e5+7;
typedef long long ll;
inline ll read() {
int ret=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-f;ch=getchar();}
while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
return ret*f;
}
int n, m, a[maxn];
//segment tree
struct seg{int l,r,sum,id;}t[maxn*100];
int cnt, rt[maxn];
inline void pushup(int x){
t[x].sum = t[lson].sum + t[rson].sum;
}
void add(int &x, int l, int r, int pos, int v){
if(!x) x = ++cnt;
if(l == r){
t[x].id = v;
++t[x].sum;
return;
}
if(pos <= mid) add(lson, l, mid, pos, v);
else add(rson, mid+1, r, pos, v);
pushup(x);
}
int ask(int x, int l, int r, int k){
if(!x || t[x].sum < k){
return 0;
}
if(l == r){
return t[x].id;
}
if(t[lson].sum >= k) return ask(lson, l, mid, k);
else return ask(rson, mid+1, r, k-t[lson].sum);
}
int merge(int x, int y, int l, int r){
if(!x){
if(l == r) t[x].id = t[y].id;
return y;
}
if(!y) return x;
if(l == r){
t[x].sum += t[y].sum;
return x;
}
lson = merge(lson,t[y].l,l,mid);
rson = merge(rson,t[y].r,mid+1,r);
pushup(x);
return x;
}
//并查集
int f[maxn];
int get(int x){
if(f[x] == x) return f[x];
return f[x] = get(f[x]);
}
int main(){
n = read(), m = read();
for(int i = 1; i <= n; ++i){
f[i] = i;
a[i] = read();
add(rt[i], 1, n, a[i], i);
}
int ans, aa, bb;
for(int i = 1; i <= m; ++i){
aa = read(), bb = read();
aa = get(aa), bb = get(bb);
if(aa == bb) continue;
f[bb] = aa;
rt[aa] = merge(rt[aa],rt[bb],1,n);
}
int q = read(); char c;
while(q--){
cin >> c;
aa = read(), bb = read();
if(c == 'B'){
aa = get(aa), bb = get(bb);
if(aa == bb) continue;
f[bb] = aa;
rt[aa] = merge(rt[aa],rt[bb],1,n);
}else{
aa = get(aa);
ans = ask(rt[aa],1,n,bb);
printf("%d
",ans?ans:-1);
}
}
return 0;
}