总述
状压dp就是利用计算机二进制的性质来描述状态的dp
| & | 按位与 | 如果两个相应的二进制位都为1,则该位的结果值为1,否则为0 |
| l | 按位或 | 两个相应的二进制位中只要有一个为1,该位的结果值为1 |
| ^ | 按位异或 | 若参加运算的两个二进制位值相同则为0,否则为1 |
| ~ | 取反 | ~是一元运算符,用来对一个二进制数按位取反,即将0变1,将1变0 |
| << | 左移 | 用来将一个数的各二进制位全部左移N位,右补0 |
| >> | 右移 | 将一个数的各二进制位右移N位,移到右端 的低位被舍弃,对于无符号数,高位补0 |
1- 判断一个数字x二进制下第i位是不是等于1
if(((1<<(i−1))&x)>0)
2- 将一个数字x二进制下第i位更改成1
x=x|(1<<(i−1))
3- 把一个数字二进制下最靠右的第一个1去掉
x=x&(x−1)
旅行商问题TSP
题意
给定一个n个顶点组成的带权的有向图的距离矩阵d(i,j),要求从0开始结果所有点一次回到0,求经过边的总权重的最小值,(2≤n≤15,0≤d(i,j)≤1000)
画个样例方便理解,比如n=5,如图
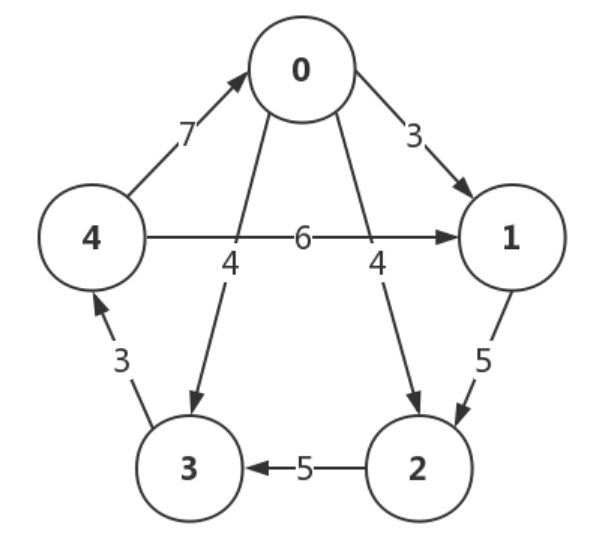
所有可能路线一共有 !n 种,就算本题的 n 很小了 !n 还是很大
可能有人会想到跑最短路,但是最短路不保证走遍每一个点,而即使我们加上了点的计数,那也不能保证不成环
其实求最小值的状压甚至可以被一些优秀的随机化算法,比如模拟退火水过,不过这些算法最怕的就是求所有状态,而状态压缩DP就做到了求出所有状态这一点
把起点0当作还未访问过的顶点,假设现在已经访问过的顶点的集合为S,当前所在的顶点为v,dp(S,v)表示现在从v出发访问剩余的所有顶点,最终回到顶点0的路径的权重的总和的最小值,集合V表示为所有城市的集合,从0到0就是路程为0

假设从v出发可以移动到任意一个节点u,d(v,u)表示v到u点的权值,显然u不属于S,所以就有:

这里涉及到集合表示和处理的问题,用set效率相对较低,但我们可以在二进制位中逐位保存某个点“存在”和“不存在”的情况,这只需涉及到二进制的位运算,速度很快,这里S或运算u表示讲u加入到集合S中
判断u是否存在于集合S中的话,那么只需要判断S∨(2^u)( 也就是S&(1<<u) )是否为真就可以了
dp[S][v]=min(dp[S][v],dp[S|1<<u][u]+d[v][u]);
S|1<<u的效果是把u点加入S集合
例题
洛谷1171
Traveling by Stagecoach
描述
旅行家所在国家有m个城市(2≤m≤30),有一个人从某个城市要到另一个城市消耗一张车票
旅行家一共有n(1≤n≤8)张车票,每张车票上记录有这次行程使用的马匹的数量
第i张车票上马的匹数是ti (1≤ti≤10),一张车票只能用一次
一个城市到另一个城市移动的时间=路程(1≤路程≤100)/马匹的数量
求a城到b城的最短时间(1≤a,b≤m),无法到达输出impossible
考虑一下:现在在城市 v,此时还剩下的车票的集合为S 的状态,我们用dp [S] [v] 表示,在这个状态出发,使用一张车票 i∈S 移动到相邻城市u,就能转移到 现在在城市 u,此时还剩下的车票的集合为S{i} (就是集合S删去元素i,理性理解下) 这个状态
把上面的状态转移看作一条边,边上的权就是 (v-u路长)/ti,由于车票不断消耗,所以这个图实质上是DAG,就变成了DAG上求最短路
if(使用车票)
dp[S & ~(1 << i)][u] = min( dp[S & ~(1 << i)][u], dp[S][v]+v到u路长/t[i] )