结果
B组 C/C++ 河北 第一名
赛情
莫名其妙就到比赛时间了,没有啥特别准备,考场在自己学校,没啥心情波动
吸取去年没东西吃的教训,这次买了一个面包和一瓶酸奶,居然要二十块 555
A: 空间
问题描述
小蓝准备用 (256MB) 的内存空间开一个数组,数组的每个元素都是 (32) 位二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 (256MB) 的空间可以存储多少个 (32) 位二进制整数?
解答
(256MB=256*2^{10}KB=256*2^{20}B=256*8*2^{20}Bit=2147483648Bit)
(2147483648Bit/32=67108864)
答案:67108864
B: 卡片
问题描述
小蓝有很多数字卡片,每张卡片上都是数字 (0) 到 (9)。
小蓝准备用这些卡片来拼一些数,他想从 (1) 开始拼出正整数,每拼一个,就保存起来,卡片就不能用来拼其它数了。
小蓝想知道自己能从 (1) 拼到多少。
例如,当小蓝有 (30) 张卡片,其中 (0) 到 (9) 各 (3) 张,则小蓝可以拼出 (1) 到 (10),但是拼 (11) 时卡片 (1) 已经只有一张了,不够拼出 (11)。
现在小蓝手里有 (0) 到 (9) 的卡片各 (2021) 张,共 (20210) 张,请问小蓝可以从 (1) 拼到多少?
提示:建议使用计算机编程解决问题。
解答
使用 (cnt[]) 数组记录手上剩余的不同数字的卡片数,用 while 循环迭代每一个待拼的数,按位拆分后依次在 (cnt) 减去
当发现 (cnt[i]) 数量不足时,说明当前数字无法拼出,跳出循环,答案为前一个拼好的数字
代码如下
#include <bits/stdc++.h>
using namespace std;
int cnt[11],c=0;
bool fl=false;
int main() {
for (int i=0;i<=9;i++) cnt[i]=2021;
while (!fl && ++c) {
int t=c;
while (t) cnt[t%10]--,t/=10;
for (int i=0;i<=9;i++)
if (cnt[i]<0) { fl=true; break; }
}
printf("%d",c-1);
return 0;
}
答案:3181
C: 直线
问题描述
在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上,那么这些点中任意两点确定的直线是同一条。
给定平面上 (2 × 3) 个整点 ({(x, y) | 0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}),即横坐标是 (0) 到 (1) (包含 (0) 和 (1)) 之间的整数、纵坐标是 (0) 到 (2) (包含 (0) 和 (2)) 之间的整数的点。
这些点一共确定了 (11) 条不同的直线。
给定平面上 (20 × 21) 个整点 ({(x, y) | 0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z}),即横坐标是 (0) 到 (19) (包含 (0) 和 (19)) 之间的整数、纵坐标是 (0) 到 (20) (包含 (0) 和 (20)) 之间的整数的点。
请问这些点一共确定了多少条不同的直线。
解答
数据范围比较小,先不考虑斜率为 (0) 或不存在的情况,直接用 (O(n^2*m^2)) 的枚举两个点组成的其他直线,
每找到一条新的直线都用数组存起来,使用点斜式 (y-y_0=k(x-x_0)) 标识直线,
遇新直线的时候逐个判断是否与先前重复(先判断斜率是否相同,再判断点是否在直线上,即代入表达式值为 (0))。
最后答案要加上斜率不存在的 (n) 条和斜率为 (0) 的 (m) 条
代码如下
#include <bits/stdc++.h>
#define N 20
#define M 21
#define eps 0.00001
using namespace std;
struct Line { double x,y,xl; };
vector<Line> v;
int main() {
for (int i=0;i<N;i++) {
for (int j=0;j<M;j++) {
for (int k=0;k<N;k++) {
for (int l=0;l<M;l++) {
if (i==k || j==l) continue;
double xl=double((1.0*(l-j))/(1.0*(k-i)));
bool fl=true;
for (int g=0;g<(int)v.size();g++) {
if ((abs(v[g].xl-xl)<eps) && (abs(double(j)-v[g].y-(v[g].xl*(double(i)-v[g].x)))<eps))
{ fl=false; break; }
}
if (fl) v.push_back((Line){double(i),double(j),double(xl)});
}
}
}
}
cout<<(int)v.size()+N+M;
return 0;
}
答案:40257
D: 货物摆放
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有 (n) 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆 (L、W、H) 的货物,满足 (n = L × W × H)。
给定 (n),请问有多少种堆放货物的方案满足要求。
例如,当 (n = 4) 时,有以下 (6) 种方案:(1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1)。
请问,当 n = (2021041820210418) (注意有 (16) 位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
解答
这么大的 (n) 也太恐怖了,一般方法做的话复杂度是要 (O(logn)) 以下的,但是太困难了
于是想着先把 (n) 分解质因数看看,代码跑出来质因数数列是 (2,3,3,3,17,131,2857,5882353),发现只有 (8) 个
要使长宽高的乘积为 (n),上述数列的每个数都要被分别分配到三个维度,这个过程可以用 (dfs) 实现,注意要去重(考试用的 vector,重载 set 也可以)
代码如下
#include <bits/stdc++.h>
#define ll long long
#define MAXN 1000007
using namespace std;
ll n,x=1,y=1,z=1; int vis[9]={0,2,3,3,3,17,131,2857,5882353};
struct node {
ll a,b,c;
bool operator == (const node &T) const {
return a==T.a && b==T.b && c==T.c;
}
};
vector<node> s;
void dfs(int now) {
if (now==9) {
bool fl=true;
node tp=(node){x,y,z};
for (int i=0;i<(int)s.size();i++) {
if (s[i]==tp) { fl=false; break; }
}
if (fl) s.push_back(tp);
return;
}
x*=vis[now],dfs(now+1),x/=vis[now];
y*=vis[now],dfs(now+1),y/=vis[now];
z*=vis[now],dfs(now+1),z/=vis[now];
}
int main() {
dfs(1);
cout<<(int)s.size()<<'
';
return 0;
}
答案:2430
E: 路径
问题描述
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图中的最短路径。
小蓝的图由 (2021) 个结点组成,依次编号 (1) 至 (2021)。
对于两个不同的结点 (a, b),如果 (a) 和 (b) 的差的绝对值大于 (21),则两个结点之间没有边相连;如果 (a) 和 (b) 的差的绝对值小于等于 (21),则两个点之间有一条长度为 (a) 和 (b) 的最小公倍数的无向边相连。
例如:结点 (1) 和结点 (23) 之间没有边相连;结点 (3) 和结点 (24) 之间有一条无向边,长度为 (24);结点 (15) 和结点 (25) 之间有一条无向边,长度为 (75)。
请计算,结点 (1) 和结点 (2021) 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题。
解答
题意已经说得很明白了,就是判断两个点之间是否符合连边条件,如果符合就连一条指定长度的边
看知乎上有些选手把最小公倍数(lcm)看成最大公因数的(gcd)做了,这样错了有点可惜
公式:(lcm(a,b)=a*b/gcd(a,b))
考场上 Dijkstra 写了一小半了发现这个似乎这个用 Floyd 跑时间是够的,反正最后交的也是一个答案
吐槽一下考场的 Dev C++ 版本太旧,同一个主进程只能 fork 一个程序窗口,跑 Flyod 的时候不能运行其他代码
#include <bits/stdc++.h>
#define MAXN 3007
#define ll long long
using namespace std;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a; }
ll d[MAXN][MAXN];
vector<ll> G[MAXN];
int main() {
memset(d,0x3f,sizeof(d));
for (int i=1;i<=2021;i++) d[i][i]=0;
for (ll i=1;i<=2021;i++)
for (ll j=1;j<=2021;j++)
if (abs(i-j)<=21) d[i][j]=d[j][i]=i*j/gcd(i,j);
for (ll k=1;k<=2021;k++)
for (ll i=1;i<=2021;i++)
for (ll j=1;j<=2021;j++)
if (d[i][j]>d[i][k]+d[k][j]) d[i][j]=d[i][k]+d[k][j];
cout<<d[1][2021];
return 0;
}
答案:10266837
F: 时间显示
问题描述
小蓝要和朋友合作开发一个时间显示的网站。在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 (1970) 年 (1) 月 (1) 日 (00:00:00) 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入格式
输入一行包含一个整数,表示时间。
输出格式
输出时分秒表示的当前时间,格式形如 (HH:MM:SS),其中 (HH) 表示时,值为 (0) 到 (23),(MM) 表示分,值为 (0) 到 (59),(SS) 表示秒,值为 (0) 到(59)。时、分、秒不足两位时补前导 (0)。
对于所有评测用例,给定的时间为不超过 (10^{18}) 的正整数
样例
样例输入 1
46800999
样例输出 1
13:00:00
样例输入 2
1618708103123
样例输出 2
01:08:23
解答
考场上很笨比,老是以为秒和毫秒之间是 (60) 或 (100) 的关系,搞了半天搞不出样例的答案
第 (N) 次做的时候突然才发现 (1s=1000ms),计算时分秒直接除对应的倍数再模一下就可以了
代码如下
#include <bits/stdc++.h>
#define ll unsigned long long
using namespace std;
ll ms,s,m,h;
int main() {
cin>>ms;
s=ms/1000,m=ms/(1000*60),h=ms/(1000*60*60);
s%=60,m%=60,h%=24;
if (h<10) cout<<"0",cout<<h<<":";
if (m<10) cout<<"0",cout<<m<<":";
if (s<10) cout<<"0",cout<<s;
return 0;
}
G: 砝码称重
问题描述
你有一架天平和 (N) 个砝码,这 (N) 个砝码重量依次是 (W_1, W_2, · · · , W_n)。
请你计算一共可以称出多少种不同的重量?
注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 (N)。
第二行包含 (N) 个整数:(W_1, W_2, W_3, · · · , W_N)。
输出格式
输出一个整数代表答案。
样例
输入
3
1 4 6
输出
10
样例说明
能称出的 (10) 种重量是:(1、2、3、4、5、6、7、9、10、11)。
(1 = 1;)
(2 = 6 − 4) (天平一边放 (6),另一边放 (4));
(3 = 4 − 1;)
(4 = 4;)
(5 = 6 − 1;)
(6 = 6;)
(7 = 1 + 6;)
(9 = 4 + 6 − 1;)
(10 = 4 + 6;)
评测用例规模与约定
对于 (50\%) 的评测用例,(1 ≤ N ≤ 15)。
对于所有评测用例,(1 ≤ N ≤ 100),(N) 个砝码总重不超过 (100000)。
解答
还算比较简单的 DP,用 (f[i][j]) 表示使用前 (i) 个砝码,能否称出重量为 (j) 的物品,值为 (1) 则可以,(0) 则不可以
对于每个状态,我们只需要关注砝码两边的差值,不需要关注两边具体的数值
那么状态转移方程为 (f[i][j]=max(f[i-1][j],f[i-1][abs(j-s[i])],f[i-1][j+s[i])),对应以下四种情况
((1)) 取 (f[i-1][j]):不使用 (s[i])
((2)) 取 (f[i-1][abs(j-s[i])]) 并且 (j>=s[i]):将 (s[i]) 放在 (j-s[i]) 的一边
((3)) 取 (f[i-1][abs(j-s[i])]) 并且 (j<s[i]):将 (s[i]) 放在空的一边
((4)) 取 (f[i-1][j+s[i]]) :将 (s[i]) 放在空的一边
三种候选码如果有任意一个为 (1),那么 (f[i][j]=1)
这个数组可以滚动,但是要注意每次新得到的需要用数组保存起来等内循环结束再赋值给 (f),防止用一块砝码使用两次
一开始看错了数据范围,看成了单个砝码的重量不超过 (100000),想着这样空间受不了,于是用 set 记录当前称出的重量了一遍,后来才改回用数组来的
代码如下
#include <bits/stdc++.h>
#define MAXN 107
#define MAXM 1000007
using namespace std;
int ans,sum,n,w[MAXN];
bool f[MAXM*10];
vector<int> v;
int main() {
cin>>n,f[0]=true;
for (int i=1;i<=n;i++) cin>>w[i],sum+=w[i];
for (int i=1;i<=n;i++) {
v.clear();
for (int j=0;j<=sum;j++) {
if (f[j]) {
v.push_back(abs(j-w[i]));
v.push_back(j+w[i]);
}
}
for (int i=0;i<(int)v.size();i++) f[v[i]]=true;
}
for (int i=1;i<=sum;i++) if (f[i]) ans++;
cout<<ans;
return 0;
}
H: 杨辉三角形
问题描述
下面的图形是著名的杨辉三角形:
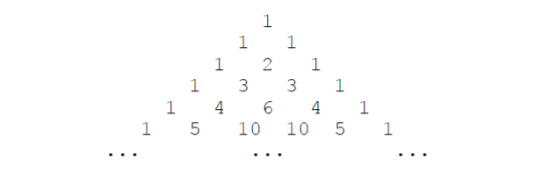
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
(1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...)
给定一个正整数 (N),请你输出数列中第一次出现 (N) 是在第几个数?
输入格式
输入一个整数 (N)。
输出格式
输出一个整数代表答案。
样例
输入
6
输出
13
评测用例规模与约定
对于 (20\%) 的评测用例,(1 ≤ N ≤ 10);
对于所有评测用例,(1 ≤ N ≤ 1000000000)。
解答
这个题做得最不好惹,先尝试数学推导发现搞不出来啥规律,做着做着就犯傻觉得 (O(n^2)) 推一个组合数就可以出来了
(原因是算了以下 (C_{2000}^{1000}) 大于 (1000000000),就觉得 (2000) 阶把全部数据范围覆盖了,笨比了233)
正解肯定是数学方法,等知道了再来补充
代码如下(错误的)
#include <bits/stdc++.h>
#define ll long long
#define MAXN 2007
using namespace std;
ll n,C[MAXN][MAXN];
int main() {
cin>>n,C[0][0]=1;
for (int i=1;i<MAXN;i++) {
for (int j=1;j<=i;j++) {
C[i][j]=C[i-1][j]+C[i-1][j-1];
if (C[i][j]==n) {
cout<<i*(i-1)/2+j;
return 0;
}
}
}
return 0;
}
I: 双向排序
问题描述
给定序列 ((a_1, a_2, · · · , a_n) = (1, 2, · · · , n)),即 (a_i = i)。
小蓝将对这个序列进行 (m) 次操作,每次可能是将 (a_1, a_2, · · · , a_{qi}) 降序排列,或者将 (a_{qi}, a_{qi+1}, · · · , a_n) 升序排列。
请求出操作完成后的序列。
输入格式
输入的第一行包含两个整数 (n, m),分别表示序列的长度和操作次数。
接下来 (m) 行描述对序列的操作,其中第 (i) 行包含两个整数 (pi, qi) 表示操作类型和参数。
当 (pi = 0) 时,表示将 (a_1, a_2, · · · , a_{qi}) 降序排列;当 (pi = 1) 时,表示将 (a_{qi}, a_{qi+1}, · · · , an) 升序排列。
输出格式
输出一行,包含 (n) 个整数,相邻的整数之间使用一个空格分隔,表示操作完成后的序列。
样例
输入
3 3
0 3
1 2
0 2
输出
3 1 2
样例说明
原数列为 ((1, 2, 3))。
第 (1) 步后为 ((3, 2, 1))。
第 (2) 步后为 ((3, 1, 2))。
第 (3) 步后为 ((3, 1, 2))。与第 (2) 步操作后相同,因为前两个数已经是降序了。
评测用例规模与约定
对于 (30\%) 的评测用例,(n, m ≤ 1000);
对于 (60\%) 的评测用例,(n, m ≤ 5000);
对于所有评测用例,(1 ≤ n, m ≤ 100000,0 ≤ ai ≤ 1,1 ≤ bi ≤ n)。
解答
显然对于前 (30\%) 的数据只需要进行 (m) 次 sort
考虑到数列中的数取值范围是 ([1,n]) ,可以用一个数组 (num[i]) 记录数字 (i) 在数列中的位置
对于 (pi==0) 的情况,在内循环中找到位置小于等于 (qi) 的数并记录,即记录 (num[i]<=qi) 的所有 (i),用 (tong[]) 标识
然后按真实值的正序遍历 (tong[val]==true) 的数,分别赋予新的位置值,(cnt) 每次减一,这样就完成了一次降序排序
(pi==1) 的情况类似处理即可,最后输出的时候要 for (int i=1;i<=n;i++) pri[num[i]]=i; 改变一下结构
这样做时间复杂度是 (O(n*m)),可以过掉前 (60\%) 的数据
#include <bits/stdc++.h>
#define MAXN 5007
using namespace std;
int n,m,num[MAXN],pri[MAXN];
bool tong[MAXN];
int main() {
cin>>n>>m;
for (int i=1;i<=n;i++) num[i]=i;
while (m--) {
for (int i=1;i<=n;i++) tong[i]=false;
int pi,qi; cin>>pi>>qi;
if (!pi) {
for (int i=1;i<=n;i++)
if (num[i]<=qi) tong[i]=true;
int cnt=qi;
for (int i=1;i<=n;i++)
if (tong[i]) num[i]=cnt--;
}
else {
for (int i=1;i<=n;i++)
if (num[i]>=qi) tong[i]=true;
int cnt=qi;
for (int i=1;i<=n;i++)
if (tong[i]) num[i]=cnt++;
}
for (int i=1;i<=n;i++) pri[num[i]]=i;
}
for (int i=1;i<=n;i++) pri[num[i]]=i;
for (int i=1;i<=n;i++) cout<<pri[i]<<" ";
return 0;
}
J: 括号序列
问题描述
给定一个括号序列,要求尽可能少地添加若干括号使得括号序列变得合法,当添加完成后,会产生不同的添加结果,请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号。
例如,对于括号序列 (((()),只需要添加两个括号就能让其合法,有以下几种不同的添加结果:(()()()、()(())、(())()、(()())) 和 (((())))。
输入格式
输入一行包含一个字符串 (s),表示给定的括号序列,序列中只有左括号和右括号。
输出格式
输出一个整数表示答案,答案可能很大,请输出答案除以 (1000000007) (即 (10^9 + 7) ) 的余数。
输入
((()
输出
5
评测用例规模与约定
对于 (40\%) 的评测用例,(|s| ≤ 200)。
对于所有评测用例,(1 ≤ |s| ≤ 5000)。
解答
想了一半没做出来的 DP...因为没有存代码,只能回忆起考场上的一些思路
要尽可能少得添加括号,所以添加的括号只可能是左右中的一种,并且数量为原字符串中左右括号数量差值
对于添加右括号的情况,用 (f[i][j]) 表示前 (i) 个字符,添加 (j) 个右括号的本质不同的添加后结果数
但是由于前 (i) 的左右括号差值是一定的,所以转移时 (j) 的范围也被限定了
添加左括号的话需要从后往前做,其他是一样的
状态转移方程在考场上写假了,以后再来补