Dp test solution
按照难易程度排序题解;
Problem B
Problem Description
Tarzan 现在想要知道,区间 [L,R] 内有多少数是优美的。我们定义一个数是优美的,这个数字要满足在它 C 进制下的各位数字之和可以整除这个数字本身。 Tarzan 不会做这道题,他希望你能帮他求出这个问题的答案。
Input format
第一行三个十进制正整数 L,R,C, L 和 R 给的是十进制形式
Output format
一行一个整数表示被认为优美的数的数量
Examples
| input 1 | output 1 |
|---|---|
| 5 15 10 | 7 |
| input 2 | output 2 |
|---|---|
| 2 100 2 | 29 |
Constrains and Notes
对于 30% 的数据满足: R - L ≤ 100000
对于另外 10% 的数据满足: C = 2
对于另外 20% 的数据满足: C = 10
对于 100% 的数据满足: 1 ≤ L ≤ R ≤ 10^18; 2 ≤ C ≤ 15
然后这道题是据说最简单的数位dp(但是我写炸了,只拿了暴力30
反正我太难了;
大致的思路:
如果一味枚举数字的话,我们没有办法边求边取模,从而不能很好的设计状态。因此我们需要考虑优化:
我们可以注意到一个数的数字之和是很小的,那么我们可以枚举这个数字之和sum,然后考虑有多少数数字之和是sum并且被sum整除;
设 $f[i][sum][rest] (表示到了第 i位,当前还没有被选满的数位和是 sum(也就是之前选择的数位之和剩下的),数字对枚举的和取模是 rest,考虑枚举这位是多少。假设为 x,最终的和为 S: )f[i][sum][rest]+ = f[i − 1][sum - x][(rest + x*p[i])%S]$
因为几个数相加%S每个数%S相加再%S,因此我们可以把每一位%S的值相加然后再%S,其中p[i]表示C^(i-1)是多少;
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll A,B;
int C;
int a[70],na,b[70],nb,p[70];
int mod;
ll f[70][400][400];
ll query(int *a,int i,int sum,int rest,bool o) //o is limits
{
if (sum<0) return 0;
if (i==0) return sum==0&&rest==0 ? 1:0;
if (!o&&f[i][sum][rest]!=-1) return f[i][sum][rest];
ll ans=0;
int up=o ? a[i] : C-1;
for (int j=0;j<=up;j++)
ans+=query(a,i-1,sum-j,(rest+mod+j*p[i]%mod)%mod,o&&j==up);
if (!o) f[i][sum][rest]=ans;
return ans;
}
int main()
{
// freopen("B.in","r",stdin);
// freopen("B.out","w",stdout);
scanf("%lld%lld%lld",&B,&A,&C);
B--;
while (A) a[++na]=A%C,A/=C;
while (B) b[++nb]=B%C,B/=C;
//printf("na=%d
",na);
memset(f,-1,sizeof(f));
ll ans=0;
for (int i=1;i<=na*C;i++)//A is max!
{//枚举数字和 sum
mod=i;
p[1]=1;
for (int j=2;j<=na;j++) p[j]=p[j-1]*C%mod;//记录C^j
ans+=query(a,na,mod,0,true)-(nb==0 ? 0:query(b,nb,mod,0,true));
for (int x=0;x<=na;x++)
for (int y=0;y<=i;y++)
for (int z=0;z<=mod;z++) f[x][y][z]=-1;
}
printf("%lld",ans);
return 0;
}
Problem C
Problem Description
Tarzan 非常烦数轴因为数轴上的题总是难度非常大。不过他非常喜欢线段,因为有关线段的题总是不难,讽刺的是在一个数轴上有 n 个线段,Tarzan 希望自己喜欢的东西和讨厌的
东西不在一起,所以他要把这些线段分多次带走,每一次带走一组,最多能带走 k 次。其实就是要把这些线段分成至多 k 组,每次带走一组,问题远没有那么简单,tarzan 还希望每次选择的线段组都很有相似性,我们定义一组线段的相似性是组内线段交集的长度,我们现在想知道最多分成 k 个组带走,Tarzan 最多能得到的相似性之和是多少?
Input format
第一行两个整数 n 和 k。
接下来 n 行每行两个整数 Li, Ri 表示线段的左右端点。
Output format
一行一个整数,表示最多能得到的相似性之和是多少。
Examples
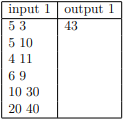
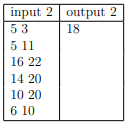
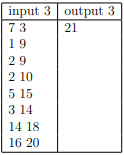
Constrains and Notes
对于 20% 的数据满足:n ≤ 8; k ≤ 5
对于 40% 的数据满足:k, n ≤ 12;
对于 70% 的数据满足:n ≤ 100
对于 100% 的数据满足:1 ≤ k ≤ n ≤ 6000, 1 ≤ Li < Ri ≤ 10^6
如果有空集:那么最多只有一组空集。我们假设存在空集的话,就是找前k-1长的算答案即可。再求剩余的 maxL 和 minR,即可算出交集的大小。
如果没有空集的话。我们再观察一个性质,对于一个完全可以包含另一个线段 B 的线段 A,A 肯定是要和 B 在一个组的。放别的组,肯定不优。
所以我们就把所有不被任何其他线段包含的 B 线段集合拿出来。假设有 M 个。然后这样的一组线段排序之后就是左端点升序的同时右端点也升序了。(假设右端点不是升序的显然就又出现了被包含的线段)这样的话我们选出的每一个集合,就是连续的一段线段了。看上去就能 dp 了。
设(dp[i][j])表示前i个线段选了j个集合,首先我们要保证此时没有空集;
(dp[i][j]=max(dp[x][j-1]+r[x+1]-l[i]|r[x+1]>l[i]))
枚举一个x,表示把前x个分成j-1个集合的最大相似性之和,然后第x+1个线段到第i个线段分成一个集合,因为线段是左右端点同时递增的,因此这一段的相似度之和就是第x+1个线段的右端点-第i条线段的左端点。

然后将l[i]提到外面来,又是一个滑动窗口;
Problem A
Problem Description
有一天 Tarzan 写了一篇文章,我们发现这文章当中一共出现了 n 个汉字,其中第 i 个汉字出现了 ai 次,因为 Tarzan 不希望文章被别人偷看,他要给这 n 个字分别用一个特殊的字符串表示,其中每一个字符串由两类字符组构成,一类是 a,另一类是 ha,例如 ahaha 就是由 a、 ha 和 ha 构成的,我们希望帮助 Tarzan 给每个汉字一个独一无二的字符串,其中不能存在两个字符串一个是另一个的前缀。我们同时希望文章尽量短,太长会把女神惹烦,文章长度就是每一个汉字出现次数乘以对应字符串的长度之和,请输出最短的文章长度。
Input format
第一行一个整数 n 表示汉字数量。
第二行 n 个整数,分别表示每个汉字的出现次数。
Output format
一行一个整数表示最短的文章长度。
Examples
| input 1 | output 1 |
|---|---|
| 3 2 1 1 | 9 |
| input 2 | output 2 |
|---|---|
| 4 1 2 3 4 | 27 |
Constrains and Notes
对于 15% 的数据满足: n ≤ 15
对于 40% 的数据满足: n ≤ 100
对于 70% 的数据满足: n ≤ 400
对于 100% 的数据满足: 3 ≤ n ≤ 750; 1 ≤ ai ≤ 100000,数据保证存在一定的阶梯性
这道题可是复杂啊:
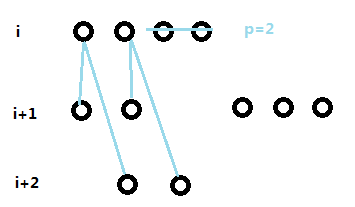
首先我们可以想到其实这道题是棵树!:
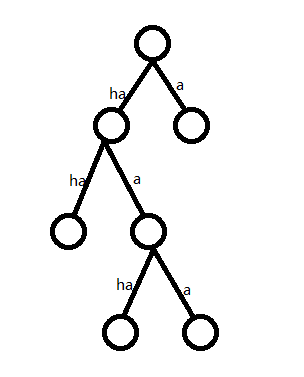
然后这道题的实际就是在这棵很神仙的树上面选择n个没有祖先后代关系(实际上就是叶子结点)的结点所需要的最少层数(我们把ha看做两层,a看做一层)
然后显然层数最少的要分配给汉字出现次数最多的,层数最多的要分配给汉字出现次数最少的;所以显然要先从大到小的sort每个汉字有多少个。
显然任意一棵有n个叶子的树都是一种方法,那么我们的目的就是找到一个最少的。
我们从n开始找:
设(dp[i][x][y][k])表示目前计算的是第i层,第i层目前有x个结点(是发展成叶子还是继续向下长我们不确定),第i+1层有y个结点,第i层之前(不计算第i层)已经确定有k个叶子结点的最小长度;
转移的话,我们枚举一个p,表示i这一层我们将其中的p个结点设置为叶子,那么(dp[i][x][y][k]=min(dp[i+1][y+x-p][x-p][k+p]+sum[n]-sum[k+p]);)
为什么sum[n]-sum[k+p]要放在右边而不是左边:四维的不是很懂,但是三维的很好想。
这里sum[i]表示前i个汉字的总个数:
for (int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
那么我们来理解一下上面那式子;
首先第i层有p个结点被确定为叶子了,那么第i+1层的k显然要在i层的基础上+p;
然后转移后的x,就变成了第i+1层的结点数:因为第i层有x个结点,其中p个结点被限制不能再生长了,那么还能生长的就是剩下的x-p个结点。每个结点增长一个ha和一个a,因为ha算两层,所以由第i层贡献的,第i+1层的结点数,就在原来的基础上增加了x-p个,那么第i+1层的总结点数就是y+x-p;
转移后y的位置:变成了i+2层的结点数,那么由第i层贡献的,就是增长为ha的所有结点,同样也只有x-p个,而当前为第一次转移(因为某一层的结点只能有它的上一层和上上层转移过来,所以可以保证上上层的转移是第一次转移),因此第i+2层的节点数就是x-p;
时间复杂度O(n^5)
显然炸掉了,考虑降维优化:
尝试把第一维优化掉
(dp[x][y][k])表示最后一行是y个结点,上一层有x个结点的情况;
(dp[x][y][k]=min(dp[y+x-p][x-p][k+p]+sum[n]-sum[k+p]);)
为什么sum[n]-sum[k+p]要放在右边而不是左边:(满口胡扯
考虑转移,我们由状态(dp[y+x-p][x-p][k+p])转移到(dp[x][y][k])可用的点数减少了,也就是有更多的点被确定为叶子了,所以需要加上这些确定为叶子的点的贡献不对呀,叶子没有贡献啊
时间复杂度O(n^4)
考虑优化转移:
每次枚举一个p,未免太浪费时间,我们可以考虑这样转移:每次把其中的一个变成叶子,这样如果想达到枚举p的效果,只需要减去多次1即可,或者直接将所有的结点向下继续建树;
(dp[x][y][k]=min(dp[x-1][y][k+1],dp[y+x][x][k]+sum[n]-sum[k]);)
(不知道是不是这么写)
然后乱七八糟,本来懂了现在懵的一匹;
代码也没看懂(滚动数组真的神仙
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<map>
#include<cassert>
#include<bits/stdc++.h>
using namespace std;
const int N=755;
typedef unsigned int uint;
const uint inf=(1u<<31)-1;
uint n,a[N],sum[N];
bool cmp(uint x,uint y) {return x>y;}
uint dp[2][N][N];int r;
int main()
{
// freopen("A.in","r",stdin);
// freopen("A.out","w",stdout);
scanf("%u",&n);
//assert(3<=n && n<=750);
for (int i=1;i<=n;i++) scanf("%u",&a[i]),assert(1<=a[i] && a[i]<=100000);
sort(a+1,a+n+1,cmp);
for (int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
for (int x=0;x<N;x++)
for (int y=0;y<N;y++) dp[0][x][y]=dp[1][x][y]=inf;
dp[r=0][0][0]=0;
for (int k=n-1;k>=0;k--)
{
for (int y=n-k;y>=0;y--)
for (int x=n-k-y;x>=0;x--) {
dp[r^1][x][y]=
min(inf,x==0&&y==0?inf:
min(
y==0?inf:dp[r][x][y-1],
x+y+y+k>n?inf:sum[n]-sum[k] + dp[r^1][y][x+y]
)
);
// if(x==1&&y==1)cout<<"dp["<<r<<"]["<<x<<"]["<<y<<"]:"<<dp[r^1][x][y]<<endl;}
/* for (int x=0;x<=n-(k+1);x++)
for (int y=0;y<=n-(k+1)-x;y++) dp[r][x][y]=inf;*/
r^=1;//Space complexity youhua?
}
printf("%u
",sum[n]+dp[r][1][1]);
return 0;
}