前言
1:与树或图的生成树相关的动态规划。
2:以每棵子树为子结构,在父亲节点合并,注意树具有天然的子结构。这是很优美的很利于dp的。
3:巧妙利用Bfs或Dfs序,可以优化问题,或得到好的解决方法。
4:可以与树上的数据结构相结合。
5:树形Dp的时间复杂度要认真计算,部分问题可以均摊复杂度分析。
6:一般设f[u]表示u子树的最优价值或者是说方案数。
或者(f[u][k])表示u子树附加信息为k的最优值,往往是通过考虑子树根节点的情况进行转移
树上最大独立集
给你一棵大小为n的树,求这棵树的最大独立集是多少。
最大独立集指的是一个最大的点集使得其中的点两两没有边相连。
N<=100000
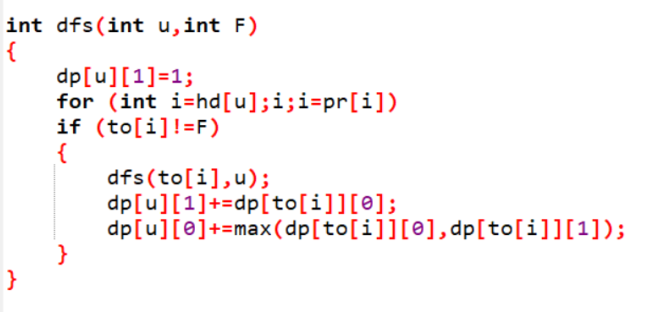
(dp[i][0/1])表示做完了i的子树, i点否/是选的最大独立集,即可直接转移。
(dp[i][0]=sum_{jin son(i)}max(dp[j][0],dp[j][1]);)
(dp[i][1]=sum_{jin son(i)}dp[j][0])
树的直径
给你一颗点数为n的树,让你求这棵树的直径是多少,也就是求最长的两个点之间的距离。
N<=100000
神仙做法:先任意一点i dfs,然后找到距离此点最远的点,然后再从这个点进行dfs,找到除去i点之外的最长路径,这两条路就是树的直径了。
随便找一个点bfs求它的最远点,设为x,再从x跑一遍bfs,求x最远点y,则(x,y)就是一个直径了。
考虑离每一个点最远的点肯定是直径的其中一个端点。
树形dp做法:(first[i])表示i点到叶子结点的最长路径。
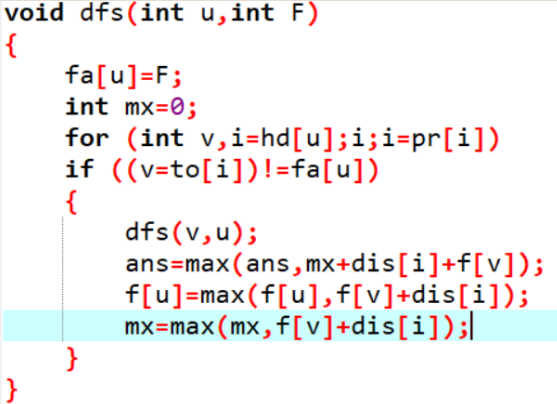
设f[i]表示i这个点到子树里面的最远点是多远的,然后对于每一个点u求出以这个点为根的最远路径距离,直接找{f[son_i]+edge_i}的前两大值加起来即可。然后再在每一个点构成的答案里面取最大值就是全局的最优值了。
#### 其他的一些简单问题
1:一棵无向树,结点为n(<=10,000),删除哪些结点可以使得新图中每一棵树结点数小于等于n/2。也就是求重心。
2:树的覆盖集,求最少选几个点能覆盖所有边,也就是不存在一条边两边点都没被选。(本质?)
3:最大权独立集?
其实都是一样的。
Tree chain problem
给定一棵有n 个点的树,以及m 条树链,其中第i 条树链的价值为wi,请选择一些没有公共点的树链,使得价值和最大。
n,m<=1000
考虑树形DP,设f(x)为以x为根的子树内选取不相交树链的价值和的最大值,枚举一条LCA为x 的链(u,v,w),那么当前方案的价值为w+ 去除u 到v 路径上的点后深度最小的点的f的和。
复杂度O(MN)设dp[i]dp[i]为以第ii个点位根节点的子树的最优解,sum[i]sum[i]表示表示ii节点的所有子节点的dpdp和(注意:不包括ii)1.第i个节点上不出现链,那么dp[i]=∑(dp[k]∣k为i的子节点)dp[i]=∑(dp[k]∣k为i的子节点);2.第i个节点上出现链,如果选择加入这条链,那么dp[i]=w(链的权值)+∑(dp[k]∣k为链上的节点的子节点)=w+∑(sum[k]∣k为链上的节点)−∑(dp[k]∣k为链上的节点)dp[i]=w(链的权值)+∑(dp[k]∣k为链上的节点的子节点)=w+∑(sum[k]∣k为链上的节点)−∑(dp[k]∣k为链上的节点)树链剖分优化可以做到O(Mlog(n)^2)
BZOJ1864 三色二叉树
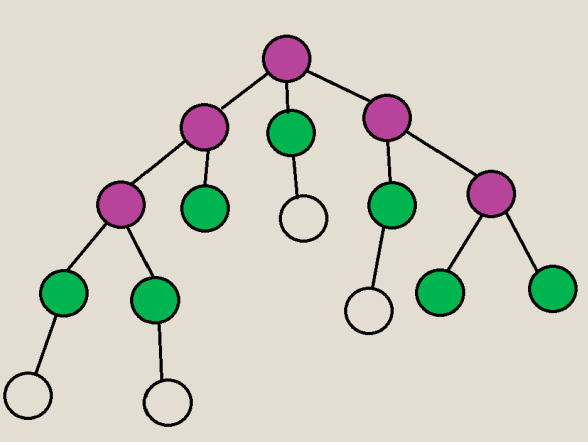
给出了一棵二叉树,点数为n,然后要求每个点和其左儿子和其右儿子三者两两之间颜色互不相同,求最多能有多少点被染成绿色。
N<=10^5
(f[i][0] ,f[i][1],f[i][2])分别表示根是绿红蓝三种颜色时的最多/最少绿色的数量,转移的时候只要保证上面的约束就行,并不难。

bzoj2466
图论中的树为一个无环的无向图。给定一棵树,每个节点有一盏指示灯和一个按钮。如果节点的按扭被按了,那么该节点的灯会从熄灭变为点亮(当按之前是熄灭的),或者从点亮到熄灭(当按之前是点亮的)。并且该节点的直接邻居也发生同样的变化。
开始的时候,所有的指示灯都是熄灭的。请编程计算最少要按多少次按钮,才能让所有节点的指示灯变为点亮状态。
对于100%的数据,满足1 <= n <=100。
设(f[i][0/1][0/1])表示在点i,i按不按,i亮不亮时,i的子树都被点亮的最少次数
1.如果摁x,那么x的儿子都不亮;如果不摁x,那么x的儿子都要亮
2.如果x发亮,那么它和它的儿子中一定有奇数个点摁了;如果x不亮,那么它和它的儿子中一定有偶数个点摁了。
我们可以设置一个辅助数组gx[i]=0/1表示当前已经选取的是否是偶数
然后对于代码真的是不会写啊;
树上背包简化版
给出一棵n个点的有根树,每个节点都是一个物品,具有价值Vi,如果一个物品要被选择,那么它的父亲必须被选择。
求选择至多m个物品的最大价值和。
n<=1000。
合并:

(f[i][j])表示在以i为根子树中选择, i强制选择,选择j个点的最大价值,转移时每次将一个孩子暴力合并到父亲上,合并就枚举这个孩子内部选择了多少点即可。
$ f[i][j]=max(f[i][j-k]+f[son][k] |k=0…(j-1))$,就是枚举son内选了多少点。这里是指枚举某个子树选择了k个点,然后将其与其他子树合并。
我们按照一般的分析复杂度的方式的话是:状态数N^2*转移复杂度N,总复杂度是O(N^3)。
实际上我们考虑每次合并的时候相当于是一组点对数量的复杂度,总的来看的话就是n个点点对的数量,均摊复杂度O(N^2)。
bzoj4033: 树上染色
有一棵点数为N的树,树边有边权。给你一个在0~N之内的正整数K,你要在这棵树中选择K个点,将其染成黑色,并将其他的N-K个点染成白色。将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。
问收益最大值是多少。
N<=1000
考虑边的贡献:两端黑点数量的乘积+两端白点数量的乘积。
定义状态(f[i][j])表示i号节点为根节点的子树里面有j个黑色节点时最大的贡献值。
然后我们要知道的就是i到其父亲这条边会计算次数就是:子树中白色节点数∗子树外白色节点数+子树中黑色节点数∗子树外黑色节点数。
这条边的贡献和i的各个孩子的子树内各有多少黑点是无关的,所以我们可以做背包求出来每个点子树内有j个黑点时贡献和是多少。

树上背包
给出一棵n个点的有根树,每个节点都是一个物品,具有价值Vi和重量Wi,如果一个物品要被选择,那么它的父亲必须被选择。
求限制重量m内的最大价值和。
n<=1000,m<=1000。
最朴素的做法
这里不是选点的数量而是重量,所以这里的朴素做法是O(n^3)
(f[i][j])表示在以i为根子树中选择, i强制选择,重量为j的最大价值,转移时每次将一个孩子暴力合并到父亲上,合并就枚举这个孩子内部选择了多少的重量即可。
(F[i][j]=max{(f[i][j-k]+f[son][k] |k=0…(j-1)})),就是枚举son内用了多重量。
注意我们这里两个一维数组的背包合并是n^2的,所以慢。
但一个一维数组和一个单独的物品合并是线性的。
DFS序上做DP
◦在dfs序上Dp,如果不选一个点,则跳过代表他的子树的dfs上连续一段。
◦设(f[i][j])表示dfs序上第i个点到第n个点,选了j的重量得到的最大的价值是
多少。 i可以选也可以不选。不选的话就要跳过整个子树。
◦设T[i]表示dfs序为i的点标号。
◦不选:$ f[i + size[ T[i] ] ][j]$
◦选: (f[i+1][ j- w[ T[i] ]]+v[ T[i] ])
◦两种情况取最大值即可
另一个奇妙的方法
不会;
bzoj5123
◦求一棵 [1,n] 的线段树的最大匹配数目与方案数。
◦ N<=10^18
树形dp+记忆化搜索
◦设$ f[l][r] (表示根节点为 [l,r] 的线段树,匹配选择根节点的最大匹配&方案
数,) g[l][r] $表示根节点为 [l,r] 的线段树,匹配不选择根节点的最大匹配&
方案数。那么这是一个很普通的树形dp。
◦注意到区间长度相等的线段树的结果是一样的,且每层至多有两种区间
长度不同的区间(打表或者推推式子都行),因此直接以区间长度为状态进
行记忆化搜索即可
然后咱这里记录的:
(f[u][1/0])表示u和自己的某个孩子匹配/不和自己的某个孩子匹配的最大匹配数量,
那么(f[u][0]=max(f[s1][1],f[s1][0],f[s2][1],f[s2][0]))
(f[u][1]=max(f[s1][0],f[s2][0])+f[sx][1])其中x表示max两者中取值较小的一个的下标
基环树
处理方法:
1:断开环上一条边,枚举边端点的情况,然后当树来处理。
2:先把环上挂着的树的信息都计算完,然后转化为序列问题,或者说是
环形的序列问题。
dfs找环
基环树,环是关键,所以做这类题目我们首先得找到环。
找环的方式很多,这里讲解dfs找环。
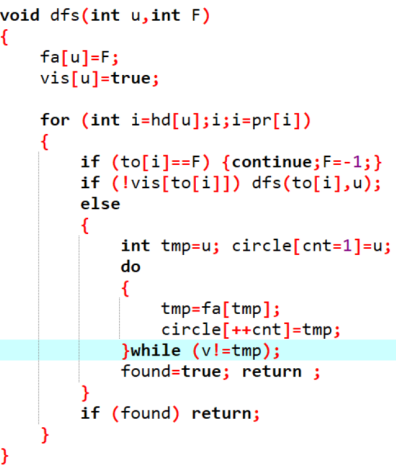
对于dfs找环,我们就对这个基环树做dfs遍历。我们知道对于一个在图,它dfs树上的每一个返祖边(vu),和dfs树上构成的路径就会构成一个环。也就是我们只需要找到这个返祖边即可 。
主函数调用时,要枚举每一个点

因为有可能是个基环树森林。
这是很容易犯的一个坑: n个点n条边不一定是个基环树,准确来讲是基环树森林!!
如果说我们要采用断开一条边,当成树来处理。我们不需要找出来整个环,只需要找一个在环上的边,按右图写法会简便很多。

基环树内向
首先它是一个有向图,它构成类似基环树的结构,有一个特点是每个点都有且只有一个出度,并且环外的节点方向指向环内
如果题目说满足每一个点都有一个唯一出度,则本质上就是给了我们一个基环内向树森林(不只是一个基环内向树!!!!)任何一个点沿着唯一出边走都会走到环上
利用这个性质可以随便选一个点再通过一个简单循环找到基环树的环。
基环外向树
与基环内向树相反,它有且只有一个入度(基环内向树是出度),并且并且由环指向环外。
可以把所有边反向后,变成基环内向树找快速找环。
bzoj1040
N个人,每个人都有一个战斗力和一个讨厌的人(不是他本身),要求一个总战斗力最大的人的集合,满足集合内部两两不互相讨厌
N<=10^5
把这个讨厌关系的图画出来,就是个基环内向树森林,然后我们要求最大权独立集。
然后对于每棵基环树,我们寻找环,断掉其中的一边,对这条边连的两个点,枚举强制其中一点不能选 ,跑最大独立集的dp,然后就好了;
求最大独立集内向和外向和无向图毫无区别,都是相邻的不能选。
这里的基环树上有且仅有一个环,就是从任意环上一条边(u,v)断开环,分两种情况,一种是选u,不选v,一种是选v,不选u,两种情况取最大值。转化成树的话,就是那个简单的树形dp。
找环dfs找就好,或者从一个点顺着父亲一直走直到走到一个曾经走到过
的点就找到一个环了。
dfs函数:就是求一个最大权独立集,与树上的并无大的区别。
work函数:枚举断开的这条边,那一端点强制不选,取最优值。

BZOJ1791
求无向基环森林中的每棵基环树的直径之和。
点数n<=10^6
先找出环,很明显答案有两种情况。
◦ 1:在以一个环上节点为根的向外的树的直径。
◦ 2:以两个环上节点分别为根的最大深度再加上两个节点在环上距离。
◦第一种情况就是之前讲的树形dp。
◦第二种情况要处理出以环上每个节点为根的最大深度d[i],环上的点重标
号,选环上1号点作为基准点,求出s[i]表示i号点到1号点的距离, sum为
总的环长。设我们找的两个环上节点是i,j
则max( min{s[i]-s[j],sum-(s[i]-s[j]} +d[i]+d[j])即为所求,但如果暴力求是
n^2的。并没有比最开始直接枚举快多少。
◦考虑优化。
◦ 我们考虑把内部的一个min去掉,式子能看起来更清晰一些。
◦ max( min{s[i]-s[j],sum-(s[i]-s[j])} +d[i]+d[j])
◦ Max( 1: s[i]-s[j] +d[i]+d[j] | s[j]>=s[i]-sum/2,
◦ 2: sum-s[i]+s[j] +d[i]+d[j] | s[j]< s[i]-sum/2 )
◦ 考虑枚举选的两个点的后一个点i,然后求对于i,离i最远的j距离是多少,然后
对于每一个i的答案求最大值就是整个基环树的直径了。
◦ 第一种情况s[j]>=s[i]-sum/2 :求d[j]-s[j]的最大值即可,注意可选的j区间会移动,
所以这里需要单调队列。
◦ 第二种情况s[j]< s[i]-sum/2:这个可行区间只会变大,不会缩小,所以直接记录
s[j]+d[j]的最大值即可。