【暑假培训1】【知识】7.15

数据结构

下面是天天见面的：
- 栈、队列
- 堆
- 并查集
- 树状数组
- 线段树
- 平衡树 (splay)
下面是不常见的：
- 主席树
- 树链剖分
- 树套树

下面是清北学堂课程表里的：
- ST表
- LCA
- HASH

1.堆

堆的话是之前就学过的东西，也写过博客，可以带过：

【堆】好多好多基础知识【堆】【洛谷例题】p1090 p1334 p1177

STL queu中有priority_queue，默认是一个大根堆，关于如何修改priority_queu的排序顺序，可以参见：【细小碎的oi小知识点总结贴】不定时更新（显然也没人看qwq）

2.LCA：

基本用途：求树上最短路

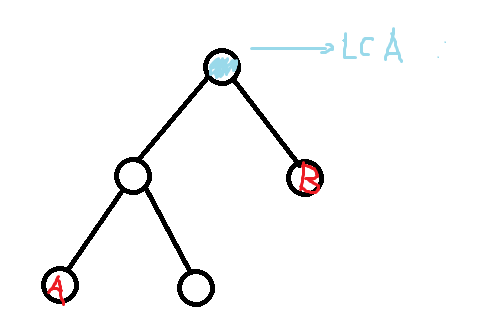
求LCA的朴素算法：

首先处理深度；

然后：

如果deep(A)<deep(B) 交换AB
把A向上抬升，到B的深度；
A和B同时上调，直到A=B；

复杂度O(deep(tree))

对于随机构造的树，可能这种算法还可以；但是当数据别出心裁构造的伐，如果退化成一条链，显然就凉凉了~；

所以我们考虑优化：

既然一个个跳不行，我们可不可以一次跳多个？

显然可以！

但是如果单纯的枚举一次跳多少个的伐，当数据够大时，我们枚举的范围可能是上百万的，也不够优；

想到，任何一个数都可以表示为二进制，也就表示每个数都可以拆成若干个2的乘方相加；

令p[x][i]表示x的2^i的祖先是谁，那么我们可以知道p[x][0]表示x的父亲，通过此可以想到递推方程： p[x][i]=p[p[x][i-1]][i-1];x的2^i祖先，等于x的2^(i-1)的祖先的2^(i-1)的祖先：

基本流程与上面相同，但是我们不再是一个一个的往上跳。从乘方最大的的开始枚举，如果跳上去以后父亲不同就往上跳，父亲相同不跳：

A和B的祖先开始是不一样的，从LCA开始，以上都一样，但是我们无法确定LCA，但是我们可以确定最后一个不一样的；

伪代码：

for i=16~0 
if(p[A][i]!=p[B][i]) A=p[A][i];B=p[B][i];

LCA一般用于解决一类可差分的问题，比如求AB之间的最短路径：求出A到根的路径，B到根的路径，减去两倍根到LCA的路径；

3.ST表：

用于求解没有修改的区间最大值问题

mx[i][j]表示从i~i+2^j-1的最大值

求一个区间[l,r]的最大值，可以拆分为两部分：

首先一个区间[l,r]，求出区间长度：k=l-r；

然后我们记录p=log₂k；

求这个区间的最大值，即为：max(mx[l][p],mx[r-2^p+1][p])；

关于mx数组的求法：递推：mx[i][j]=max(mx[i][j-1],mx[i+2^j-1][j-1]);

举个栗子：

[19,46]

k=46-19=28；p=16；ans=max(mx[19][4],mx[31][4])//可能写炸了将就着；

4.Hash：

Hash（字符串）=>int

Hash将一个字符串转换为一个int；

Hash是允许冲突的，但是我们要尽量避免冲突；

设计Hash：

1.随便取一个p，把字符串当做p进制数（建议取质数，并且是大于字符串大小的质数）

2.取字符的ASCII码*p^i（i表示此字符在此字符串中是第几位[from right to left]），然后计算一段字符串的每个字符，把值相加，就是这一段字符串的Hash值；

3.显然你看这个数会很大，可能会炸。我们可以取一个大质数mod用来取模，当然也可以用Unsigned long long强势自然溢出；

具体的处理：

求字符串，每个前缀的哈希值；

H_i：1~i的Hash值；

H_i=H_i-1*p+Si

Hash(i,j)=H_j-H_i*p^j-i+1

5.并查集：

令fa[x]表示x的父亲；树根的父亲等于本身；

查询A和B在不在一个集合中：找到A和B的根，比较是否相同；

如何将两个集合合并：

找A代表元AA,B代表元BB，令fa[AA]=BB;

路径压缩：直接指向代表元

6.树状数组：

浅谈树状数组

支持单点修改，区间查询；其实也可以区间修改，单点查询(利用差分)

所求所有问题，必须存在逆元？

主要应用：

1．线段树常数过大时

2．线段树功能过多时

可以在logn的时间内改变一个数，logn的时间求前缀和：

然后只讲代码实现，具体原理↑：

短短几行代码：

int lowbit(int x){
    return x&(-x);
}

void modify(int x,int y){
    // add y to a[x]
    for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}

int query(int x){
    // sum of a[1]...a[x]
    int ret=0;
    for(int i=x;i;i-=lowbit(i)) ret+=c[i];
    return ret;
}

int query(int l,int r){
    return query(r)-query(l-1);
}

7.线段树（抽象线段二叉树；）：

线段树小记

支持区间修改，区间查询；

主要应用：一类区间修改区间查询的问题；

Sum线段树：

先是单点修改：

确认点的位置
更新树的权值

区间查询:

任何一条线段，都可以被logn条线段覆盖；

递归看关系；

从最大的开始看，然后有关系就继续往下递归直到被完全覆盖，返回，统计进答案；

线段树的节点个数2n级别的，*4防止溢出写炸；

前置：

struct Node{
    int l,r;
    int sum;
    int tag;
}t[N<<2];

void pushup(int rt){
    t[rt].sum=t[rt<<1].sum+t[rt<<1|1].sum;
}

建树：

void build(int rt,int l,int r){
    t[rt].l=l;
    t[rt].r=r;
    if(l==r){
        t[rt].sum=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    pushup(rt);
}

单点修改a[p]=c；

void modify(int rt,int p,int c){
    if(t[rt].l==t[rt].r){
        t[rt].sum=c;
        return;
    }
    pushdown(rt);
    int mid=(t[rt].l+t[rt].r)>>1;
    if(p<=mid) modify(rt<<1,p,c);
    else modify(rt<<1|1,p,c);
    pushup(rt);
}

区间查询：

int query(int rt,int l,int r){
    if(l<=t[rt].l&&t[rt].r<=r){
        return t[rt].sum;
    }
    pushdown(rt);
    int ret=0;
    int mid=(t[rt].l+t[rt].r)>>1;
    if(l<=mid) ret+=query(rt<<1,l,r);
    if(mid<r) ret+=query(rt<<1|1,l,r);
    return ret;
}

区间修改：

懒标记：

标记这一整段线段的每一个值，都加一个特定的数；

懒惰的：先放在哪里，在没有必要下方时，就不下放：标记下放：pushdown；

Pushdown：

将此点的标记下放给左右儿子，然后自己的标记清0；

然后同时维护左右节点的区间和；

碰到这个节点就下放

void add(int rt,int l,int r,int c){
    if(l<=t[rt].l&&t[rt].r<=r){
        t[rt].tag+=c;
        t[rt].sum+=c*(t[rt].r-t[rt].l+1);
        return;
    }
    pushdown(rt);
    int mid=(t[rt].l+t[rt].r)>>1;
    if(l<=mid) add(rt<<1,l,r,c);
    if(mid<r) add(rt<<1|1,l,r,c);
    pushup(rt);
}

总结啦：

堆：最大值插入、删除、查询
ST表：区间最大值查询
树状数组：单点修改，前缀查询
线段树：区间修改，区间查询