题前废话:

然后树状数组也是用来维护前缀和的一种数据结构,对于树状数组,修改与求和都是O(nlogn)的,还是很nice的;
基本思想:
首先我们知道,对于任何一个数i,都可以分解成几个不同(指x的值不同)的2^x,那么对于一段区间[1,n],我们可以按照n的二进制分解将这个大区间分成几个小区间:
n=(10101)2,可以将区间[1,n]分解成为三个小区间:
①长度为24的小区间[1,24]
②长度为22的小区间[24+1,24+22]
③长度为20的小区间[24+22+1,24+22+20]
对于区间[1,x],树状数组将其分为logx个区间;
然后这些区间的区间长度:若区间结尾为R,则区间长度就等于R的“二进制分解”下最小的2的次幂,设它为lowbit(i);
然后开一个数组c,c[i]记录着序列a的区间[i-lowbit(i)+1,i]所有数之和。
以下是一个树状数组的结构图示:
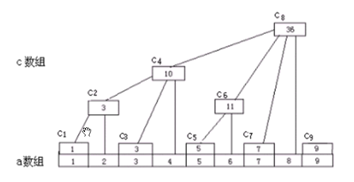
几个部分:
1.求lowbit:
我……不是很想写证明因为我也不会,直接记录一下怎么求吧:
int lowbit(int x){ return x&(-x); }
2.对某个元素进行单点修改操作;
对某个数i加上y,首先我们找到c[i],显然c[i]肯定包含数i,先将c[i]加上y,然后找c[i]的所有祖先(每次加上lowbit(当前节点)),全都加上y;
void add(int x,int v){ while(x<=n){ c[x]+=v; x+=lowbit(x); } }
3.对某个区间进行查询:
树状数组只支持查询1~x的值(好像就是前缀和?),因此当要查询区间的值时,我们需要用区间右端点的前缀和-(区间左端点-1)的前缀和;
查询操作:
int Sum(int x){ int res=0; while(x>0){ res+=c[x]; x-=lowbit(x); } return res; }
了解了这几个基本操作,我们就可以做板子题:【模板】树状数组 1了:
完完全全套上面的板子就可以了,然后对了还有一点,我们大可不必将序列的值单独再开一个数组去存,可以将其当做是一个开始全为0的树状数组,然后输入x就相当于在第i个数+x;
#include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch<='9'&&ch>='0') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m,a; int c[500007]; int lowbit(int n){return n&(-n);} void add(int x,int v){ while(x<=n){ c[x]+=v; x+=lowbit(x); } } int Sum(int x){ int res=0; while(x>0){ res+=c[x]; x-=lowbit(x); } return res; } int main(){ n=read();m=read(); for(int i=1;i<=n;i++) a=read(),add(i,a); int ops,x,y; for(int i=1;i<=m;i++){ ops=read();x=read();y=read(); if(ops==1) add(x,y); if(ops==2) printf("%d ",Sum(y)-Sum(x-1)); } return 0; }
然后既然有树状数组1,肯定至少有树状数组2,树状数组2是单点查询区间修改,还不至于变态,可以用差分来做;
首先先是暴力,直接for循环将x~y间的每个数都+k;
虽然知道妥妥的TLE,但我还是试了试雷:

#include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch<='9'&&ch>='0') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m,a; int c[500007]; int lowbit(int n){return n&(-n);} void add(int x,int v){ while(x<=n){ c[x]+=v; x+=lowbit(x); } } int Sum(int x){ int res=0; while(x>0){ res+=c[x]; x-=lowbit(x); } return res; } int main(){ n=read();m=read(); for(int i=1;i<=n;i++) a=read(),add(i,a); int ops,x,y,k; for(int i=1;i<=m;i++){ ops=read();x=read(); if(ops==1) { y=read(); k=read(); for(int i=x;i<=y;i++) add(i,k); } if(ops==2) printf("%d ",Sum(x)-Sum(x-1)); } return 0; }
首先介绍一下差分:
差分,顾名思义,肯定要做差;
举个栗子:
已知序列a[6]={1,8,4,2,5,6},它的差分数组b[6]={1,-7,4,2,-3,-1},
如果我们将序列a的第2~第4个元素+1:
a[6]={1,9,4,3,5,6},b[i]={1,-8,4,2,-2,-1}
我们发现,变化的只有第2项和第5项(很好想明白为啥就不证明了),所以对于这个题,我们可以用树状数组维护一个差分变化量(只维护变化)数组,开始时全为0(因为较原来的数组没有区别),然后当要将某个区间[x,y]+k时,我们将差分数组的x项+k,将差分数组的y+1项-k;这样求某个数的值的时候,我们可以累加它之前的差分变化量,然后加上它自己原本的值,就是修改后的值啦;
#include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch<='9'&&ch>='0') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m,a[500007]; int c[500007]; int lowbit(int n){return n&(-n);} void add(int x,int v){ while(x<=n){ c[x]+=v; x+=lowbit(x); } } int Sum(int x){ int res=0; while(x>0){ res+=c[x]; x-=lowbit(x); } return res; } int main(){ n=read();m=read(); for(int i=1;i<=n;i++) a[i]=read(); int ops,x,y,k; for(int i=1;i<=m;i++){ ops=read();x=read(); if(ops==1) { y=read(); k=read(); add(x,k); add(y+1,-k); } if(ops==2) printf("%d ",a[x]+Sum(x)); } return 0; }
end-
