备注:作者非常菜,有不足之处请发表于讨论区,谢谢!
树形dp用于解决树上问题。
转移往往会有子树合并,以及从 u 转移到 u 的父亲 father。
它通常长这样
1 void dfs(int u,int fa){ 2 //pre();//do something 3 for (int i=head[u];i;i=Next[i]){ 4 int v=vet[i]; 5 if (v==father) continue; 6 dfs(v,u); 7 //doit();//do something 8 } 9 }
链表就不在叙述了,它大概长这样
1 inline void add(int u,int v,int va){ 2 //从u到v加一条长度为va的边 3 Next[++edge_num]=head[u]; 4 head[u]=edge_num; 5 vet[edge_num]=v; 6 val[edge_num]=va; 7 }
其中先讲一些比较简单的例子:
树的直径:
给定一棵树,树中每条边都有一个权值,树中两点之间的距离定义为连接两点的路径边权之和。
树中最远的两个节点之间连接这两点的路径被称为树的直径,即直径是一个数值概念,也可代指一条路径
$d[u]$表示$u$到以$u$为根节点的子树中任意一个孩子的距离的最大值
$d[u]=displaystylemax_{v in Son(u)}(d[v]+val[i])$其中$val[i]$表示$u$到$v$的距离
那么答案就是$displaystylemax_{vin Son(u)}(d[u]+d[v]+val[i])$其中$val[i]$表示$u$到$v$的距离
有些人可能会有疑惑,万一$u$为根节点到任意一个孩子的距离的最大值经过$v$呢,其实也很好处理,我们只需要先统计答案,再更新$d[u]$就可以了
void dfs(int u,int fa) { for(int i=head[u];i;i=Next[i]) { int v=vet[i]; if(v==father) continue; dfs(v,u); int w=val[i]; ans=max(ans,d[u]+d[v]+w); d[u]=max(d[u],d[v]+w); } }
两遍dfs版:第一遍找最远点 第二次从最远点出发找最远点的最远点 两个点的距离便是树的直径
找树的直径只需要先从一个点(随便是什么)遍历,找到距离它最远的一个点,那么这个点肯定就是树的直径的一端了,从找到的这一端再遍历一次,找到距离这个端点最远的点,这个点就是另外一端了
洛谷P1352 没有上司的舞会
题目描述
某大学有N个职员,编号为1~N。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数Ri,但是呢,如果某个职员的上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入输出格式
输入格式:
第一行一个整数N。(1<=N<=6000)
接下来N行,第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)
接下来N-1行,每行输入一对整数L,K。表示K是L的直接上司。
最后一行输入0 0
输出格式:
输出最大的快乐指数。
输入输出样例
5
题解
我们发现,用一个数组已经无法解决这道题目了,所以,我们可以用$2$个数组
$f[u][0]$表式以$x$为根节点中$u$不参加时快乐指数总和的最大值,此时$x$的下属可以参加也可以不参加
$f[u][0]=$ $displaystylesum_{vin Son(u)}max(f[v][0],f[v][1])$
$f[u][1]$表式以$x$为根节点中$u$参加时快乐指数总和的最大值
则$f[u][1]=happy[u]+$ $displaystylesum_{vin Son(u)}f[v][0]$
$AC Code$
1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <iostream> 5 using namespace std; 6 const int N=12005; 7 int f[N][2],happy[N],Next[N],head[N],vet[N]; 8 bool has[N]; 9 int edge_num,n; 10 inline void add(int u,int v){ 11 Next[++edge_num]=head[u]; 12 head[u]=edge_num; 13 vet[edge_num]=v; 14 } 15 void dfs(int u,int fa){ 16 f[u][0]=0; 17 f[u][1]=happy[u]; 18 for (int i=head[u];i;i=Next[i]){ 19 int v=vet[i]; 20 if (v==fa) continue; 21 dfs(v,u); 22 f[u][0]+=max(f[v][0],f[v][1]); 23 f[u][1]+=f[v][0]; 24 } 25 } 26 int main(){ 27 scanf("%d",&n); 28 for (int i=1;i<=n;++i) scanf("%d",&happy[i]); 29 for (int i=1;i<n;++i){ 30 int u,v; 31 scanf("%d%d",&u,&v); 32 add(u,v); 33 add(v,u); 34 has[v]=1; 35 } 36 for (int i=1;i<=n;++i){ 37 if (!has[i]){ 38 dfs(i,0); 39 printf("%d ",max(f[i][0],f[i][1])); 40 break; 41 } 42 } 43 return 0; 44 }
P5021 赛道修建(NOIP提高组D1T3)
题目描述
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 $m$ 条赛道。
C 城一共有 $n$ 个路口,这些路口编号为 $1,2,…,n$,有 $n-1$ 条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 $i$ 条道路连接的两个路口编号为 $a_i$ 和 $b_i$,该道路的长度为 $l_i$。借助这 $n-1$ 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 $e_1,e_2,…,e_k$,满足可以从某个路口出发,依次经过 道路 $e_1,e_2,…,e_k$(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 mm条赛道中长度最小的赛道长度最大(即 $m$ 条赛道中最短赛道的长度尽可能大)
输入输出格式
输入格式:
输入文件第一行包含两个由空格分隔的正整数 $n,m$,分别表示路口数及需要修建的 赛道数。
接下来 $n-1$ 行,第 $i$ 行包含三个正整数 $a_i,b_i,l_i$,表示第 ii 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 $n-1$ 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出格式:
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
输入输出样例
7 1 1 2 10 1 3 5 2 4 9 2 5 8 3 6 6 3 7 7
31
9 3 1 2 6 2 3 3 3 4 5 4 5 10 6 2 4 7 2 9 8 4 7 9 4 4
15
说明
【输入输出样例 1 说明】
所有路口及适合于修建赛道的道路如下图所示: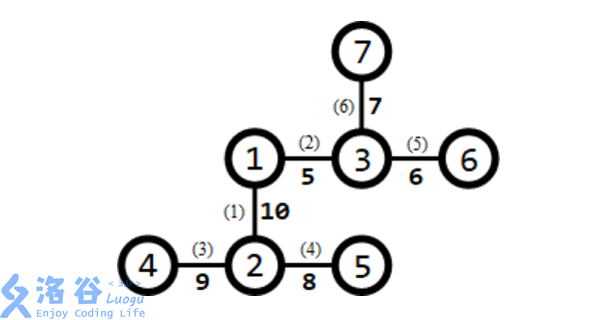
道路旁括号内的数字表示道路的编号,非括号内的数字表示道路长度。 需要修建$1$条赛道。可以修建经过第 $3,1,2,6$ 条道路的赛道(从路口 $4$到路口 $7$), 则该赛道的长度为 $9 + 10 + 5 + 7 = 31$,为所有方案中的最大值。
【输入输出样例 2 说明】
所有路口及适合于修建赛道的道路如下图所示: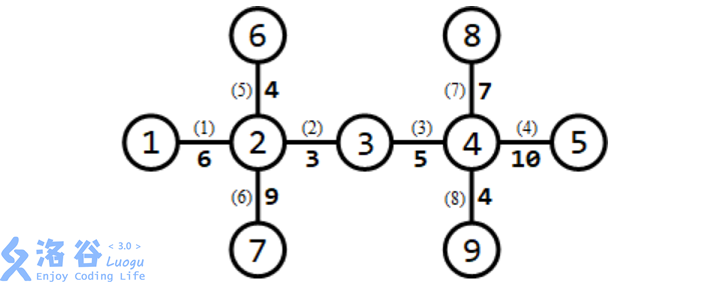
需要修建 3条赛道。可以修建如下 3条赛道:
经过第 $1,6$条道路的赛道(从路口 $1$ 到路口$7$),长度为 $6 + 9 = 15$;
经过第$5,2,3,8$ 条道路的赛道(从路口$6$ 到路口 $9$),长度为 $4 + 3 + 5 + 4 = 16$;
经过第 $7,4$ 条道路的赛道(从路口 8 到路口5),长度为 $7 + 10 = 17$。 长度最小的赛道长度为 $15$,为所有方案中的最大值。
【数据规模与约定】
所有测试数据的范围和特点如下表所示 :
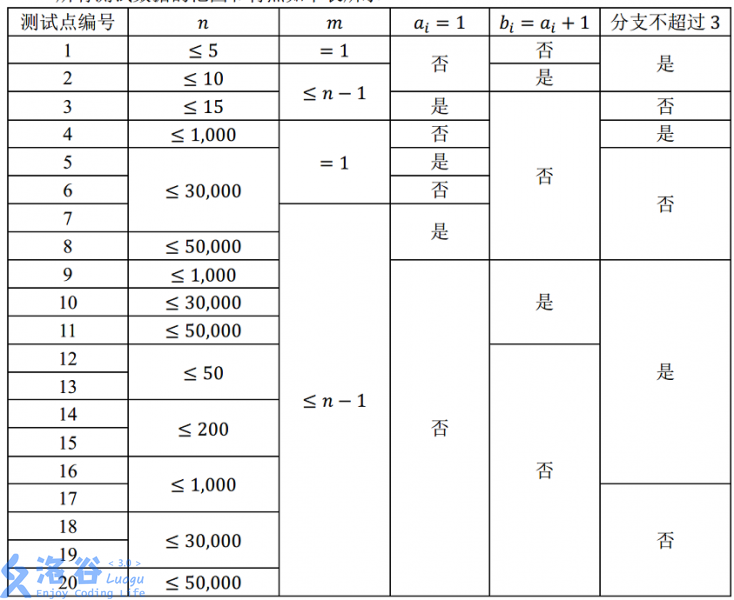
其中,“分支不超过 3”的含义为:每个路口至多有 3 条道路与其相连。 对于所有的数据,
$2 ≤ n ≤ 50,000 1 ≤ m ≤ n-1 1 ≤ a_i,b_i ≤ n 1 ≤ l_i ≤ 10,000$
题解
$noip2018 day1 T3$,听说大众分$55$分,可是我只有20分。
要求对于 $i$ 所有儿子的 $f$,在保证两两匹配数(两个半链合成一条赛道)最多的同时,向 $f_i$ 转移尽可能大的值。于是将所有 $f$ 排序贪心找到最大匹配数,然后,二分找到转移给 $f_i$ 的值。当然,用$set$更加简单明了。
讲得详细一些:
在更新$u$时,对于一个$val$,只有$2$种情况:
1.$val>=mid ans++$因为$val$不管怎么加,对答案的贡献只有1
2.$val1+val2<=mid$则对于一个$val$,找出最小的$val2$使得$val+val2>=mid$
我们可以使用$set$更加简便,讲一下大致的做法:
1.对于每一个儿子传上来的最长距离,若大一等于$mid$,则$ans++$,否则,放到一个$set$里面去
2.枚举每一个最小值$min$,二分出$>=min$的$num$
3.若找不到,则退出
4.若找到的就是它自己且当前值的只有$1$个,查找下一个
5.删去$mid and num$
6.把最大的传上去
1 // luogu-judger-enable-o2 2 #include <cstdio> 3 #include <algorithm> 4 #include <set> 5 #include <cstring> 6 using namespace std; 7 const int N=50005; 8 multiset<int> S[N]; 9 int head[N<<1],Next[N<<1],vet[N<<1],val[N<<1]; 10 int n,edge,ans,Ans,m; 11 void read(int &a){ 12 char ch=getchar();int f=0;a=0; 13 while (ch<'0'||ch>'9') f|=ch=='-',ch=getchar(); 14 while (ch>='0'&&ch<='9') a=(a<<3)+(a<<1)+ch-48,ch=getchar(); 15 a=(f==0)?a:-a; 16 } 17 inline void add(int u,int v,int va){ 18 Next[++edge]=head[u]; 19 head[u]=edge; 20 vet[edge]=v; 21 val[edge]=va; 22 } 23 int dfs(int u,int father,int mid){ 24 S[u].clear(); 25 for (register int i=head[u];i;i=Next[i]){ 26 int v=vet[i]; 27 if (v==father) continue; 28 int now=dfs(v,u,mid)+val[i]; 29 if (now>=mid) ++ans; else S[u].insert(now); 30 } 31 int loop=0; 32 while (!S[u].empty()){ 33 int min=*S[u].begin(); 34 if (S[u].size()==1) return max(loop,min); 35 //把最大的传上去 36 multiset<int>::iterator now=S[u].lower_bound(mid-min); 37 if (now==S[u].begin()&&S[u].count(*now)==1) ++now; 38 //若找到的就是它自己且当前值的只有1个,查找下一个 39 if (now==S[u].end()) 40 //找不到 41 loop=max(loop,min),S[u].erase(S[u].find(min)); 42 else { 43 ++ans; 44 S[u].erase(S[u].find(min)); 45 S[u].erase(S[u].find(*now)); 46 //删去 47 } 48 } 49 return loop; 50 } 51 int main(){ 52 read(n);read(m); 53 for (int i=1;i<n;++i){ 54 int x,y,z; 55 read(x);read(y);read(z); 56 add(x,y,z); 57 add(y,x,z); 58 } 59 int l=1,r=500000000; 60 while (l<=r){ 61 int mid=l+r>>1; 62 ans=0; 63 dfs(1,0,mid); 64 if (ans>=m) l=mid+1,Ans=mid; 65 else r=mid-1; 66 } 67 printf("%d ",Ans); 68 return 0; 69 }
洛谷P2458 [SDOI2006]保安站岗
题目描述
五一来临,某地下超市为了便于疏通和指挥密集的人员和车辆,以免造成超市内的混乱和拥挤,准备临时从外单位调用部分保安来维持交通秩序。
已知整个地下超市的所有通道呈一棵树的形状;某些通道之间可以互相望见。总经理要求所有通道的每个端点(树的顶点)都要有人全天候看守,在不同的通道端点安排保安所需的费用不同。
一个保安一旦站在某个通道的其中一个端点,那么他除了能看守住他所站的那个端点,也能看到这个通道的另一个端点,所以一个保安可能同时能看守住多个端点(树的结点),因此没有必要在每个通道的端点都安排保安。
编程任务:
请你帮助超市经理策划安排,在能看守全部通道端点的前提下,使得花费的经费最少。
输入输出格式
输入格式:
第1行 n,表示树中结点的数目。
第2行至第n+1行,每行描述每个通道端点的信息,依次为:该结点标号i(0<i<=n),在该结点安置保安所需的经费k(<=10000),该边的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号r1,r2,...,rm。
对于一个n(0 < n <= 1500)个结点的树,结点标号在1到n之间,且标号不重复。
输出格式:
最少的经费。
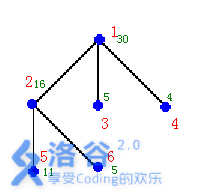
如右图的输入数据示例
输出数据示例:
输入输出样例
说明
样例说明:在结点2,3,4安置3个保安能看守所有的6个结点,需要的经费最小:25
题解
可知一个点被控制有且仅有一下三种情况:
1.被父亲节点上的保安控制
2.被儿子节点上的保安控制
3.被当前节点上的保安控制
我们设$dp[0/1/2][u]$表示$u$节点所在子树中全部被控制的最小代价
$0$表示只有$u$节点尚未被控制(等待被其父亲节点控制)
$1$表示$u$节点已经被控制,但$u$节点上没有保安
$2$表示$u$节点上有保安
$dp[0][u]=∑min(dp[1][v],dp[2][v])$显然1,2状态都是满足的
$dp[1][u]=∑min(dp[1][v],dp[2][v]) +$ 某一个$dp[2][v]$
也就是说对于其中一个儿子取$dp[2][v]$而其他儿子取$min(dp[1][v],dp[2][v])$ 及i号点必须要找一个儿子来覆盖它,其余随意。
$dp[2][u]=∑min(dp[0][v],dp[1][v],dp[2][v])+val[u]$全部可以转移。
1 #include <cstdio> 2 using namespace std; 3 const int oo=2000000000; 4 const int N=300000; 5 int f[4][N],head[N],vet[N],val[N],Next[N],edge; 6 int n; 7 inline int min(int a,int b){return a<b?a:b;} 8 inline int min(int a,int b,int c){return min(min(a,b),c);} 9 inline void Min(int &a,int b){a=(a<b)?a:b;} 10 inline void add(int u,int v){ 11 Next[++edge]=head[u]; 12 head[u]=edge; 13 vet[edge]=v; 14 } 15 void dfs(int u,int father){ 16 int sum=0;f[2][u]=val[u]; 17 for (int i=head[u];i;i=Next[i]){ 18 int v=vet[i]; 19 if (v==father) continue;dfs(v,u); 20 sum+=min(f[1][v],f[2][v]); 21 f[2][u]+=min(f[1][v],f[2][v],f[0][v]); 22 } 23 f[0][u]=sum;f[1][u]=oo; 24 for (int i=head[u];i;i=Next[i]){ 25 int v=vet[i]; 26 if (v==father) continue; 27 Min(f[1][u],sum-min(f[1][v],f[2][v])+f[2][v]); 28 } 29 } 30 int main(){ 31 scanf("%d",&n); 32 for (int i=1;i<=n;++i) { 33 int now,value,sum,son; 34 scanf("%d%d%d",&now,&value,&sum); 35 val[now]=value; 36 for (int j=1;j<=sum;++j){ 37 scanf("%d",&son); 38 add(now,son); 39 add(son,now); 40 } 41 } 42 dfs(1,0); 43 printf("%d ",min(f[1][1],f[2][1])); 44 return 0; 45 }