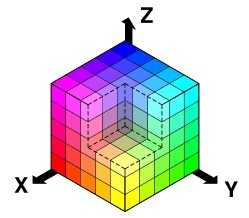
畢達哥拉斯距離
我們現在對畢達哥拉斯定理已經相當瞭解了。在前一個章節中我們知道了它並不隻是出現在三角形中;它可以應用在各種形狀中。它不隻是關於a,b,c的;它可以應用在任何有平方項的方程式中。
不隻是在沿著房間中的對角線的距離時勾股定理才有意義,它在任何舉例中都有意義,比如說我們的電影喜好與顏色的“距離”。
如果它能被測量,那麼它就可以類比到勾股定理中。讓我們看看其中的奧妙。
3.1理解勾股定理
我們都承認勾股定理成立。在任意一個三角形中:
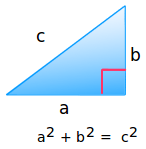
如果a=3,b=4,那麼c=5。很簡單,是吧?接下來,我們註意到一個關鍵的地方,那就是a邊與b邊是成直角的(註意那個紅色的矩形框)。在其中一個方向上移動並不影響另一個方向上的移動。
這就像南北對東西。沿著北方移動並不改變或東或西方向的移動,反之亦然——這些方向相互獨立(專業術語稱為相互正交)。
勾股定理讓我們可以找到兩個相互正交的方向之間的最短路徑。所以這並不是完全與直角“三角形”有關——而是關於比較在在直角上移動的“東西”。
你:如果我向東走三個街區,向北走4個街區,那麼最終我距離我的起始點有多遠?
我:直線距離是5個街區。根據這個距離為你的旅行准備幹糧吧。
你:呃,好吧。
3.2 那麼c是什麼呢?
我們可以認為c隻是一個數字,但是這會讓我們繼續停留在無聊的三角世界中。我會把c看作是a和b的組合。
但是它不是像加法那樣簡單的組合——畢竟,a+b並不等於c。這不隻是簡單零件的組合——勾股定理讓我們以一種類似於加法的方法把互相正交的元素組合起來。其中有諸多奧妙。
在我所舉的例子中,c是5個街區長的“距離”。但是不隻是這樣:其中包含了東方3個街區的距離,北方4個街區的距離。沿著C運動就意味著你同時向東,向北運動。很簡單的想法對吧?
3.3 勾股定理的連鎖應用
讓我們再深入一些,試著連續應用勾股定理。看看這個:
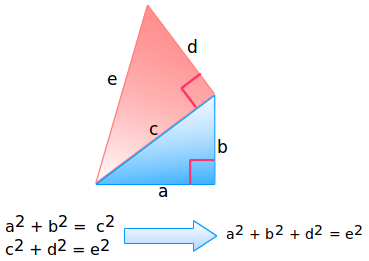
很酷吧?我們用紅色畫出了另一個三角形,其中c作為它的一條邊。因為c與d是相互正交的,我們從勾股定理就可以得到:c2 + d2 = e2 。
我們用a2 + b2 替換c2 ,就可以得到:
a2 + b2 + d2 = e2
這樣就很有意思了:我們用三個正交的項(a、b、d)表示出了e。又有了一種新的模式?
3.4 睜大眼睛,在三維世界中看看
認為兩個三角形很奇怪?試試把其中一個放到紙平面之外。不再是把它們平鋪開,把紅色三角形豎起來:
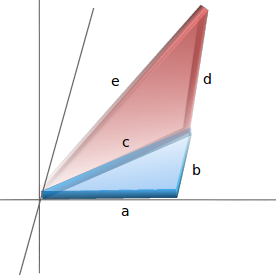
還是相同的三角形,隻是換個角度看它。但是我們現在在三維世界中!如果我們把a、b、d分別稱作x、y、z,那我們便可以得到:
x2 + y2 +z2 = 距離2
很漂亮。在數學中我們通常測量x座標(左右距離),y座標(前後距離),z座標(上下距離)。現在我們發現給定一個點的三維座標我們便可以知道它的三維距離。!
3.5 在不同的維度空間中應用勾股定理
正如你所猜想的,勾股定理可以推廣到任意的維度空間中去。那就是,你可以連續的添加三角形並計算它們的“外圍”部分:
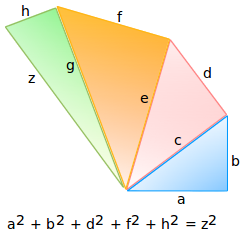
你可以想像每一個三角形都有它對應的一個維度。如果線段是成直角的,那麼勾股定理便成立並且可以計算出結果。
3.6 距離是怎樣計算出來的
勾股定理是計算兩點距離的基礎。考慮以下兩個三角形:
- 邊長分別為4,3的三角形[藍色三角形]
- 邊長分別為8,5的三角形[紅色三角形]
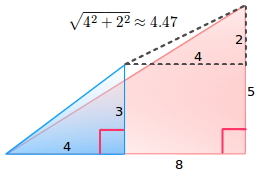
從藍色三角形的末端[座標為(4.3)]到紅色三角形的末端[座標為(8.5)]的距離為多少呢?讓我們在在兩個端點之間,通過減去對應的邊來構造一個三角形。我們所構造的三角形的斜邊就是要求的距離:
距離:(8-4,5-3) = (4,2) = sqrt(20) = 4.47
很酷是吧?在三維空間中,我們可以通過以下公式計算點(x1 ,y1 ,z1 )到點(x2 , y2 ,z2)的距離:
距離2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2
至於誰大誰小並不影響,因為它們都將被平方,所以保持非負(使用勾股定理的另一個優勢)。
3.7 怎樣計算任意的距離
勾股定理並沒有限制應用在空間距離這樣一個狹窄的範圍內。它可以應用在任意正交的維度中:空間,時間,觀影的口味,色彩,溫度。實際上,它可以應用在任意一組數字中(a,b,c,d,e)。讓我們來具體看一看。
3.8 測算用戶偏好
讓我們假設你做了一個關於觀影偏好的調查:
- 你喜歡《第一滴血》嗎?(1-10)
- 你喜歡《小鹿斑比》嗎?(1-10)
- 你喜歡《宋飛正傳》嗎?(1-10)
我們怎麼比較人們的分數呢?從而發現相似的口味?勾股定理可以幫助我們!
如果我們把分數當作一個“點”(《第一滴血》,《小鹿斑比》,《宋飛正傳》),那麼我們的調查可以這樣表示出來:
- 硬漢:(10,1,3)
- 普通人:(5,5,5)
- 敏感的人:(1,10,7)
利用勾股定理,我們可以知道不同人之間的“差異”:
- 硬漢與普通美國人的差距:(10-5,1-5,3-5)=(5,-4,-2)=6.7
- 硬漢與敏感的人的差距:(10-1,1-10,3-7)=(9,-9,-4)=13.34
正如我們所猜想的,硬漢與敏感的人之間有著很大的代溝,而與普通人的差距則較小。勾股定理幫助我們把這個距離量值化,而且在把一些相似的結果放在一起發揮了許多作用。
這個技巧幫助Netflix對電影喜好進行分類,以及其他一些類似的通過偏好進行愛好猜測的技術中(比如說亞馬遜的推薦)。用專業術語來說,我們把偏好作為一個向量,然後利用勾股定理計算他們之間的距離(然後或許彙集於此進行分類)。
3.9 發現色彩間的距離
測量色彩間的距離是另一項很有用的應用。色彩可用RGB(紅/綠/藍)法來表示。舉例來說
- 黑色(0,0,0) ——沒有顏色
- 白色(255,255,255)——每種顏色都達到最大值
- 紅色(255,0,0)——隻有紅色,沒有其他顏色
我們可以把所有顏色映射到一個“色彩空間”中,如圖所示:
我們可以用非常一般的方法得到色彩間的距離:利用RGB值得到距離黑色(0,0,0)的距離。貌似我們人眼不能區分距離四個單位的顏色;見鬼,即使是相距30個單位我看起來依然差不多:
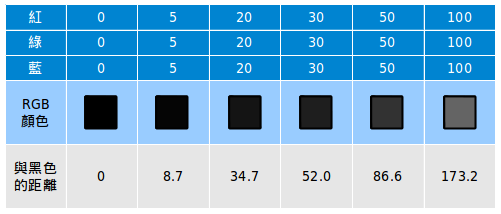
你看它們有多相似呢?色彩間的距離給了我們一種可以量化的方法來表示色彩的間的距離。你甚至可以利用色彩間的距離來整理已經模糊掉的圖像。
3.10 要點:你可以測量任何東西
如果你可以通過用一組特徵值表示,那麼你就可以利用勾股定理比較任何東西:
- 一個星期的溫度:(星期一,星期二,星期三,星期四,星期五)。通過連續的比較幾個星期的溫度來發現它們有多不同(通過五維向量進行比較)。
- 每小時,每天,或者是每週進入商店的顧客數量
- 時空關係的距離:(緯度,精度,高度,時間)。如果你在建造時間機器的話就很有用(或者是視頻游戲中會用到一些)!
- 人們之間的區別:(身高,體重,年齡)
- 公司之間的區別:(收入,盈利,市場份額)
你可以對這些距離進行不同的加權處理(比如說年齡乘以一個常數)。但是我還是要重復說一遍其中的核心要點:如果你能把它量化,那麼你就可以用勾股定理進行比較。
你的x,y,z可以代表任何數值。而你也不僅僅是在三維空間中應用它。毫無疑問,數學家喜歡告訴你其他測量距離的方法(又叫做度量空間),但是勾股定理是最有名的,而且也是一個非常棒的起點。
3.11 那麼,這裏到底發生了什麼呢?
當我們重新回顧我們被教給的概念是我們依然有很多東西要學。數學是美的,但是其中的優雅通常被埋在機械化的證明與一堆公式之中。我們不需要太多的證明;我們需要有趣的,直覺化的結果。
以勾股定理為例:
- 可以應用在任何形狀的圖形中,而不隻是三角形中(比如說圓)
- 可以應用在任何有平方項的方程中(比如說動能)
- 可以推廣到任意維數中(a2 + b2 + c2 + d2 ……)
- 可以測量任意類型的距離(比如說顏色與電影喜好之間)
對於一個有兩千多年歷史的定理來說,這個結果還不錯對吧?這些東西需要時間消化,今天就到此為止吧。希望你能享受到快樂的數學。