最近做Nvidia AI city challenge track1遇到了一个calibration问题，感觉跟仿射映射有点关系，但是感觉线代基本都不怎么记得了Orz。。。。 于是复习了一下仿射映射有关知识，现整理于此。
知识均来自于xnh老师讲授。
首先列几个定义与定理，从而使我后文叙述方便：
-------------------------------------------------------------------------- --------------
定义1：设A是域K上的仿射空间，其关联的向量空间是V，称映射A——》K是仿射线性函数如果
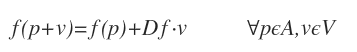
其中Df属于V*是V上的线性函数。可称它是f是线性部分或微分。仿射空间上的常值函数是线性部分为0的仿射线性函数。
注意：我这篇文章里讨论的仿射空间都是欧几里得仿射空间。即关联的向量空间V是欧几里得向量空间，度量记为 。
定义2：双射f：E——>E称为E的保距映射如果它保持距离，即对任意p,q属于E，有
定理1：内积空间V上的线性算子A是保距的当且仅当它保持内积：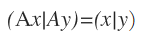
，从而当且仅当 
。
定义3：欧氏空间上的线性算子A称为正交算子如果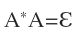 
。
（
在这里代表的是矩阵A的共轭转置，由于我们讨论的是欧氏空间，实际上就是矩阵A的转置，
是恒等变换）
定理2：映射f E-->E是运动，当且仅当，f是仿射变换且其线性部分是正交算子。
定理3：对任何的保距映射f，存在唯一确定的平面
（称之为保距映射f的轴）使得
（1）
且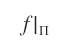 
是平移（可能是平凡的，即等于恒等变换，或 
是一个点）。
（2）Df不固定任何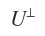 
中的非零元。
------------------------------数学语言与任氏猿语的分割线---------------------
-----------------------------精确严谨与胡言乱语的分割线-----------
一、一些理解
我觉得吧，一般的空间变换，其实分为两个部分，一个部分是平移（可以理解为移动坐标系的原点），对应f（p0），一个部分是伸缩旋转反射之类保持原点不动的变换----这部分实际上就是一个矩阵（注意零向量乘以一个矩阵肯定还是一个零向量，所以矩阵不可能移动原点）。
所谓的保距映射，是一种特殊情况，就是对于任意两个点，实施变换后两点的距离不变的映射，放在生活的中典型例子就是刚体运动，无论门怎么旋转，门上两块木头的距离不变，一个铁球管你怎么抛，无论它在天上怎么飞呀飞转啊转的，铁球内部两点间的距离可以认为是没有变化的。就是生活中所有很硬的没有弹性的东西的运动啦。反之，搓圆捏扁这种变换就不属于我这篇文章讨论的范畴。
由定理1，所有这样的保距映射的Df所对应的矩阵为正交矩阵，行列式为正负1.反过来也成立，当且仅当。
（注！：这个1大致上是指你所采取的单位制下的1，准确的说是仿射空间A所关联的向量空间V的基域K的单位元。。。mmp数学真的不讲人话）
为啥由定理1可以知道对应矩阵为正交矩阵，行列式为正负1呢？我一直觉着矩阵实际上就是代表着保持原点不动的n维空间变换，在保距的限制下，伸缩变换被排除了，那么这个矩阵代表的就是旋转与反射的复合。这个定理说的就是，一个保距的矩阵，先实施一次这个矩阵所代表的变换，再来一次这个矩阵的转置代表的变换，可以变回来。比如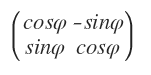
代表顺时针旋转 
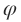，这个矩阵的转置 
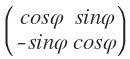代表逆时针旋转
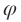，显然它们的合成是不变。
又一个矩阵的行列式跟它的转置矩阵的行列式相等，于是A的行列式的平方等于1，得到解为正负1.
其次关注一下所谓的轴。我理解里实质就是特征值为1的特征子空间。在生活中的典型例子应该是转轴，这里仿射几何定义的轴就是在保距映射f的变换下不变的n维空间，广义上的轴。它可以是个点，是条直线，是个三维空间，或更高维的空间。
顺便提一下，三维欧几里得空间的刚体运动如果有不动点，那一定是旋转，旋转轴是由运动的不动点形成的直线，而且，任何物体的移动都可以通过先沿着一个方向平移，后绕某条直线旋转来实现，也可以先旋转，后平移。
二、三维欧几里得空间下的保距映射
我们可以用轴来分析一下三维欧几里得空间的保距映射。
保距映射 f可表示为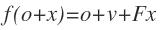
O为原来的原点，o+v为新原点，这部分是平移。设F的矩阵为A。
前面已经说明了，A必然是一个正交矩阵，行列式为1,n*n的正交矩阵虽然未必能对角化，但是可以化成标准形式：
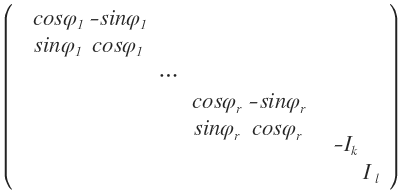
（I代表的是单位矩阵，
就是一个l*l，对角线上全是1的矩阵）
因为轴就是特征值为1的特征子空间，所以轴的维数就是A的标准形式中l的数量。也即(A-E)X=0的解空间的维数。
以轴的维数为分类标准我们可以分类讨论一下三维欧几里得空间下f可能表示的变换：
若轴的维数为3，即l=3，那么A对空间是一个恒等变换，f是一个将原点从o移动到o+v的平移。
若轴的维数为2，即l=2，,这时剩下的一个位置只可能是一个-1，所以轴是一个平面，f是通过这个平面的反射，或是一个滑动反射，即过这个平面的反射和一个平移的合成。
若轴的维数为1，即l=1，剩下两个位置是 ，这时轴是一条直线，f是绕直线的旋转，f是螺旋运动（一个绕直线的旋转与一个平移的合成）
若轴的维数为0，即l=0，这时轴是一个点，剩下三个位置可以是一个 和一个-1，这时f是镜像旋转，即绕一条直线的旋转与过一个平面的反射的合成，这个平面和这条直线垂直且交于轴点。
三、欧几里得空间上的仿射变换直观的几何意义
定理：欧几里得空间（E，V）的仿射变换f是四个变换的合成：
- 平移
- 绕某个点o的旋转
- 以o为原点的一个直角坐标系的各个轴方向做伸缩
- 一个过含o的平面的反射（如果这个仿射变换的Df的行列式为负）
证明：
首先仿射变换f可以分解为$f= t_vg$,其中$t_v$是一个平移，而g是一个保持某个点o不动的变换。
由极分解可知Dg可以分解为一个保距算子和一个正定算子的乘积（另开一帖证明），于是记Dg= DH ，其中D是保距的，H是正定的。
由于H是正定的，从而是自伴随的，在对应基下的矩阵是实对称的，实对称矩阵可对角化（另开一帖证明），从而在以o为原点的某个直角坐标系下有：
H$e_i$ = $lamdai ei$
此为在各个轴方向做伸缩。
保距算子D的几何意义在上一节中已经分析过了，虽然上一节中分析的是三维情况下的，但是高维情况下是类似的。
大致就是这样。