《principles of model checking》中的离散时间马尔科夫链

说明：此文为我自学《principles of model checking》第十章内容的笔记。

一、离散时间马尔可夫链的定义，目标问题和一些辅助定义。

二、将迁移系统转化为矩阵表达及一简例

三、列出方程X=AX+B

四、对于解该方程的一点个人想法

五、作者给出的解法

一、离散时间马尔可夫链的定义，目标问题和一些辅助定义。

一个离散时间马尔可夫链定义为一个五元组，其中

　　目标问题：求解各个状态到达给定的最终状态的概率。

　　一些辅助定义：

　　C U B(读作 C until B)：表示通过C到达B（或者说到达B的路径上的每个点都在V集合内）

　　C U (<=n)B:表示在n步及以内通过C到达B

　　另外用S1,S?,S0将S划分成三部分：

　　（我这里写的定义也原文略有不同，我把定义收紧了，方便叙述）

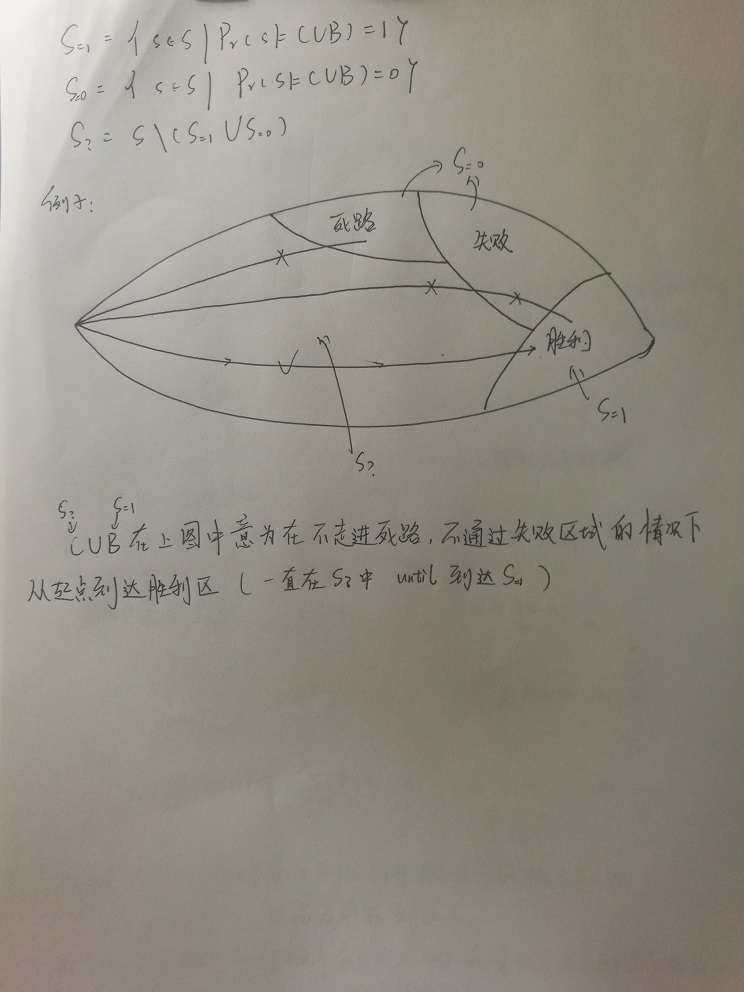
　　以下是书上这部分原文：

二、将迁移系统转化为矩阵表达及一简例

想法非常直观，将每个状态编个号然后令aij为从i到j的转移概率即可

以下是《principles of model checking》中给的一个例子。

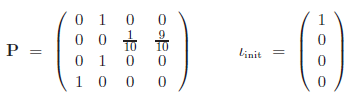
P第一行表示start，第二行表示try，第三行lost，第四行delivered。

矩阵乘以行向量的物理意义是：走一步。得到的结果是走一步之后的新概率分布。

注意：这样写的矩阵在进行乘操作时得写为行向量乘矩阵。上面那个初始向量写为列向量是与P不匹配的。

三、列出方程X=AX+B

X=AX+B这一行方程，可以求出各个状态点到达最后的胜利区域的概率。

以下是原文供参考：

　　可以发现我写的跟原文略有不同：原文中走一步后的情况分为两类：到达胜利区和未到达。将之后胜利概率为0的情况包括在未到达胜利区了。我在这里小小改动了一下主要是想着可以实现的时候缩小矩阵。

另外关于如何划分S1，S？，S0的问题：

首先胜利区域和失败区域应该是由人工指定的，并将其对应的Xs标记为1和0.从胜利区域出发逆向搜索（将图中所有边反向），取补集得到死路区。再从死路区出发搜索（这时候图里的边不反向）所有能到达的非胜利区即为问号区。

四、解方程的个人想法

作者对于如何解这个方程更多的从物理（或者说实际？）角度考虑，利用模型对应的意义给出了一个构造性解法。之后还给了一个特殊情况求逆法。

而我由于刚学完一年的线性代数，刚看到这个问题的时候主要是从纯数学的角度考虑。

X=AX+b移项后得到（I-A）X=B。这是一个线性代数基本问题，即解CX=D。先考虑是否有解，再考虑有多少解，最后考虑怎么求解或者解之间有什么关系。

设C的列向量为c1,c2,…,cn，判断CX=D是否有解等价于判断D是否可以由c1,c2,…,cn线性表出。或者说，D是否在c1,c2…,cn形成的线性子空间中。

运用矩阵工具这个问题被转化为判断C和C上D的增广矩阵是否等秩。

若rank(C)=rank(C,D)，则有解，rank(C)<rank(C,D)，则无解。不可能有rank(C)>rank(C,D)（一组基加上一个向量D生成的子空间不可能减秩）。

特殊地，如果矩阵C是满秩的，rank(C)与rank(C,D)必然相等。同时方程的解唯一（因为矩阵的逆唯一）。

在rank(C)=rank(C,D)的情况下，若C不满秩，方程有无穷解（因为有自由变量）。

于是我觉得解（I-A）X=B可以采用线性代数的方法：先计算（I-A）的秩，若满秩则用求逆算法得A的逆。将其与B相乘得到答案。不满秩再计算B的逆，判断是否有解，有解的话解出解空间找出最小可行解即可。

五、作者给出的解法

作者一共给出了两种解法，无限迭代法与一种特殊的求逆法。

无限迭代法非常有意思，简而言之是令X初始为0，用X=AX+B反复迭代直到X值不变。

以下证明这种无限迭代会产生一个单调上升并收敛的数列。并且，若X初始为0的时候得到的数列极限为最小不动点(方程X=AX+B的最小解).

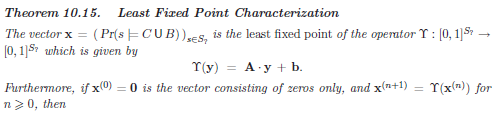
然后作者证明了只要S0确实包括且仅包括了所有绝对不可能胜利的点，那么方程就将只有唯一解。

之后作者简略叙述了唯一解的另一种证明思路。

主要讲的是A的特征值的绝对值必然小于1，从而I+A+A^2+……+A^n+……收敛

证明它就是I-A的逆，从而方程有唯一解

但是我实在没懂”by roughly the same arguments as in proof of Theorem10.15(即前文中我贴出来的原文)”是怎么证出来不存在绝对值大于等于1的特征值的。

我试图自行证明，但在证明大于-1的时候遇到了一些问题。。。。我还是把这个未完成的证明放上来，望有人指正。