一、定义
定义(约束可满足问题CSP((cal{F}))):输入时一些形式来自(cal{F})的约束(R_j),每个(R_j)作用于布尔变量(x_1,x_2,...x_n)中的若干个,是否存在一个变量的赋值(pi:{x_1,x_2,...x_n } ightarrow {0,1}),使得(pi)满足每一个约束(R_j)。
CSP问题,就是通过规定可作用变量的约束的函数集合(cal{F}),定义的对应可满足问题CSP((cal{F}))。当(cal{F})变动的时候,CSP((cal{F}))就构成一个判定问题集合。如此一来,就可以研究(cal{F})如何决定CSP((cal{F}))的计算复杂性。
二、计数问题的难解性的判定标准
判定问题3SAT,对应一个计数问题#3SAT。
定义(#3SAT问题) 输入是一个3CNF公式(varphi),(varphi)是关于布尔变量集(X = {x_1,x_2,...x_n})的,问存在多少个赋值(pi: {x_1,x_2,...x_n} ightarrow {0,1}),使得(pi)满足(varphi)。
定义(满足约束解数目问题(#CSP)):输入时一些形式来自(cal{F})的约束(R_j),每个(R_j)作用于布尔变量(x_1,x_2,...x_n)中的若干个,问存在多少个赋值(pi:{x_1,x_2,...x_n } ightarrow {0,1}),使得(pi)满足每一个约束(R_j)。即问:
定义 (#P困难性) 如果#P里的任何一个问题A都可以归约到某个问题B,则称B是#P困难的。
定理 #3SAT是#P困难的。
三、复数值域的满足约束解数目问题
四、#CSP与张量网络
定理 #(CSP(cal{F}))等价于#(cal{F}|{=_1,=_2,...,=_d...})等价于#(cal{F}cup {=_1,=_2,...,=_d,...})。
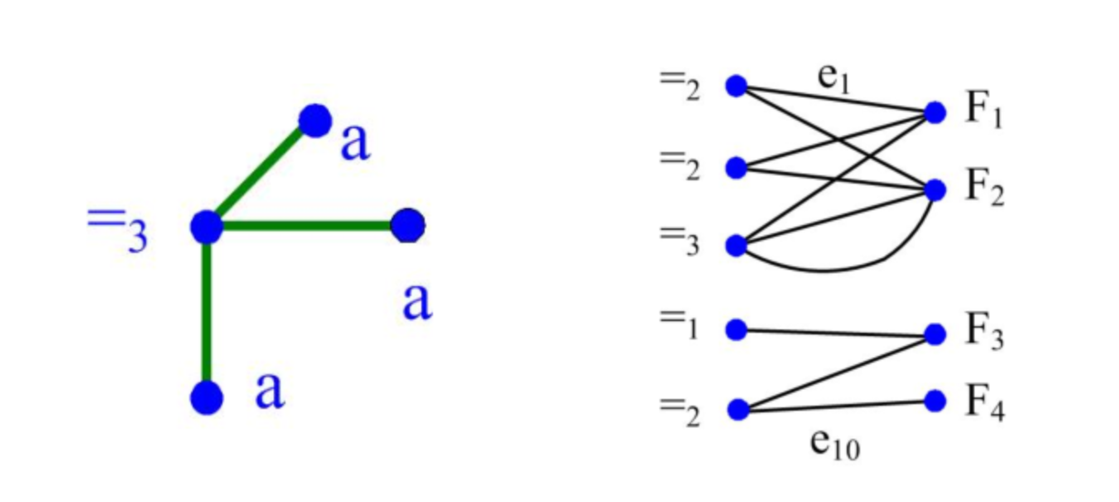
例如:三元相等函数
五、图同态数目问题
一个图(G(V_G,E_G))到图(H(V_H,E_H))的同态,是一个从(V_G)到(V_H)的映射(psi),满足对任意(e=(u,v)in E_G,(psi(u),psi(v))in E_H)。
例子如下所示:
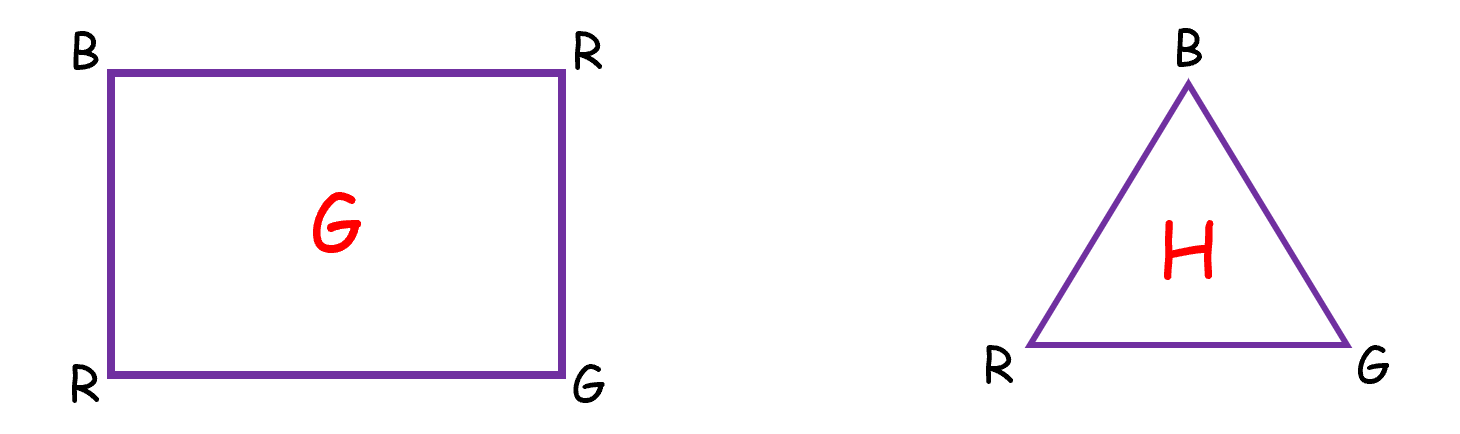
(G)中的每一定点对,都可以在(H)中找到,所以(G)是(H)的同态。下面的是图不同态的例子。
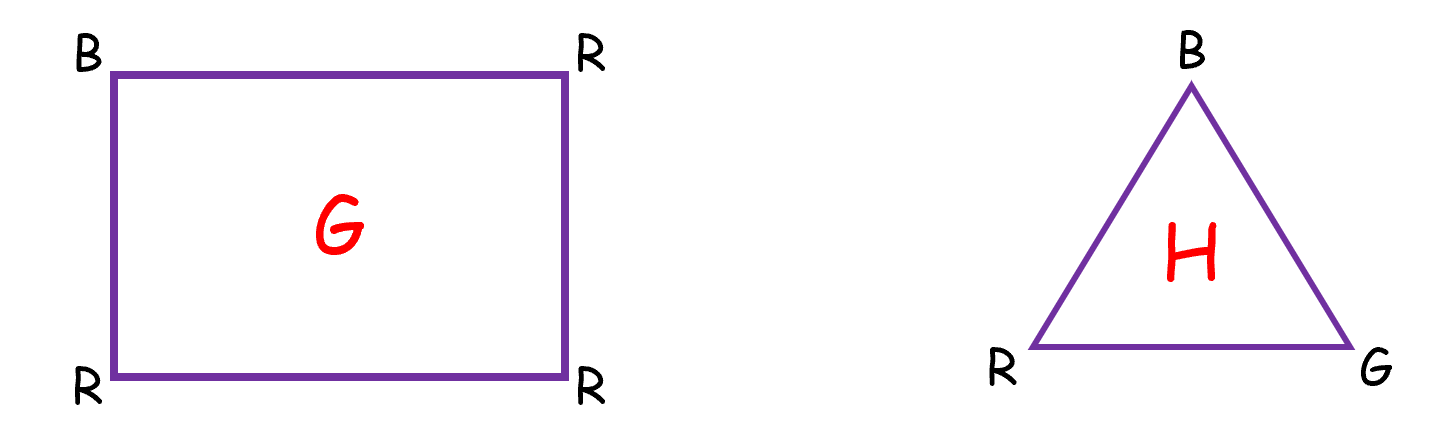
比如(G)中的(<R,R>),在(H)中找不到映射的边。其实上述图同态问题,可以转化为图三染色问题。如果(G)是(H)的同态,那么(G)一定是(H)的一个正确染色实例。
定义 (到图H的同态数目问题)输入图是G,问G到H的同态数目。图H的边关系是一个二元关系(H:V imes V ightarrow {0,1})。
图同态数目问题就是#(CSP({H}))问题。如下图所示。
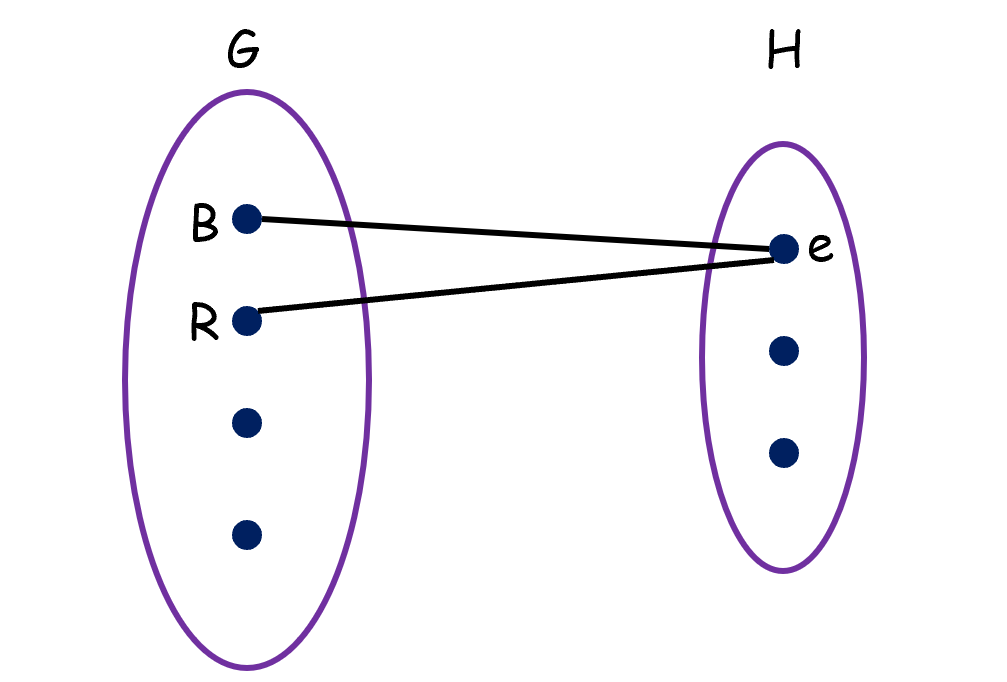
其中(H)为约束。其中(H)的连通矩阵为:
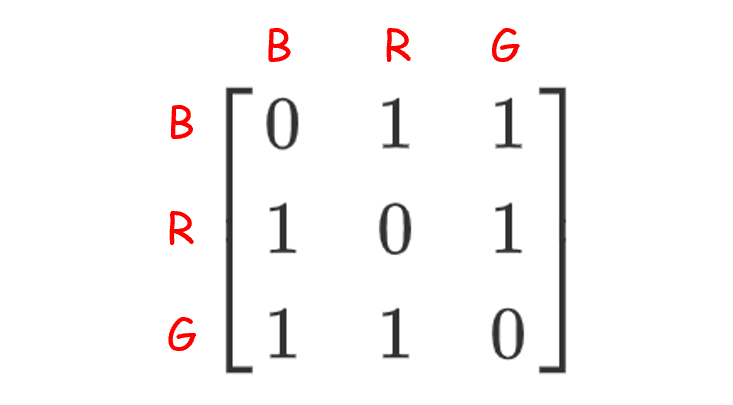
相同顶点的边不能连在一起,即为0。