张量网络

张量网络定义

1.1 封闭的张量网络

用([k])来表示一个大小为(k)的有限集，(k)代表个数，例如一个大小为(k)的有限集({1,2,3,...,k})。一个d元布尔函数(F:[2]^d ightarrow C)，在((x_1,x_2,x_3,...,x_d))的值记为(F(x_1,x_2,x_3,...,x_d))。张量网络用图描述离散函数（定义域是离散集合的函数称为离散函数。其函数图像为一系列离散的点）的结合。其中图可以允许重边和自环（出发点和终点是同一个点），不限于简单图（在无向图中，关联一对顶点的无向边如果多于1条，则称这些边为平行边，平行边的条数称为重数。在有向图中，关联一对顶点的有向边如果多于1条，并且这些边的始点与终点相同(也就是它们的的方向相同)，称这些边为平行边。含平行边的图称为多重图，既不含平行边也不包含自环的图称为简单图。）
图(G(V,E))的每一个点(v)被赋予一个(d_v)元布尔函数(F_v)，这里(d_v)表示(v)的度（某点连接的边数）。点(v)的(d_v)条边按一定的次序记为(e_{v,1},e_{v,2},...,e_{v,d_v})。张量网络的值的定义为：

[sum_{e_1,...,e_m in [2]} prod_{vin V}F_v(e_{v,1},e_{v,2},...,e_{v,d_v}) ]

其中(e_1,...,e_m in [2])中(e_1,...,e_m)表示的是一个图的边，而且边的“权重”取值为0或1。张量网络值的定义就是一个图的边取0或1，然后计算每个点连接的边“权重”的乘积(F_v)，在累加所有的点的(F_v)值。上述是一个枚举过程，一个m条边图可能有(2^m)种情况。朴素的方法是要把所有情况都列举出来，一一计算。

定义（封闭的张量网络）一个张量网络由三个要素构成：

1、图(G(V,E))。（(E={e_1,e_2,...,e_m})。顶点(v)的度记为(d_v)。）
2、每个顶点(v)被赋予一个(d_v)元的离散函数(F_v)。（函数的每个变量的定义域为(D)）。
3、每个顶点(v)的(d_v)条边被赋予一个次序，第(i)条边记为(e_{v,i})。

它的值被定义为：

[sum_{e_1,...,e_m in D} prod_{vin V}F_v(e_{v,1},e_{v,2},...,e_{v,d_v}) ]

更数学家的符号可以写为：

[sum_{sigma:E ightarrow in D} prod_{vin V}F_v(sigma(e_{v,1}),sigma(e_{v,2}),...,sigma(e_{v,d_v})) quad或 quad sum_{sigma:E ightarrow in D} prod_{vin V}F_v(sigma|Neighbor(v)) ]

定义对称函数

一个(d)元函数(F),如果对任何(d)元置换(pi)，都有(F(x_1,x_2,...,x_d) = F(x_{pi(1)},x_{pi(2)},...,x_{pi(d)}))，称(F)是对称函数。

比如：(F(1,0,0) = F(0,1,0) = F(0,0,1))

定义对称函数的简记法

一个(d)元布尔函数(F)，最多只有(d+1)种函数值，通过枚举函数值记为(F)为([F_0,F_1,...F_d])，其中(F_i)是(F)在输入是(i)个1和(d-i)个0的值。

比如(d)为3，那么有(2^3)种情况，那么根据对称函数定义，有0个1，1个1，2个1和3个1共4种情况，即(d+1)种函数值。

定义 #(cal{F})问题

输入一个所有函数都来自(cal{F})的张量网络，求它的值。

通俗的说就是在满足张量网络的前提下，在该范围求满足某定义规则的数量。

例如：

前提：(k)规则图(G(V,E))，是每个点的度都是(k)的图。
从中找一个(E^{'})，满足：1、(E^{'} subseteq E)；2、(G(V,E^{'}))是1规则图。

定义完美匹配数目问题（#(PM)）

输入一个图，求它的完美匹配数目。

例如：

(s)入(t)出的规则图，是每个点的入度都是(s)，出度都是(t)的图。有向图(G(V,E))的一个圈覆盖是一个集合(E^{'})，满足：1、(E^{'} subseteq E)；2、(G(V,E^{'}))是1入1出规则图。

定义圈覆盖数目问题（#(PM)）

输入一个图，求它的圈覆盖数目。

1.2开放的张量网络

1.2.1、张量积的定义

两个矩阵M和N的张量积M(otimes)N定义为：

[M = left ( egin{matrix} m_{11} & m_{12} & cdots & m_{1t}\ m_{21} & m_{22} & cdots & m_{2t} \ vdots & vdots & ddots & vdots \ m_{s1} & m_{s2} & cdots & m_{st} end{matrix} ight ) qquad Motimes N = left ( egin{matrix} m_{11}N & m_{12}N & cdots & m_{1t}N \ m_{21}N & m_{22}N & cdots & m_{2t}N \ vdots & vdots & ddots & vdots \ m_{s1}N & m_{s2}N & cdots & m_{st} N end{matrix} ight ) ]

设M = ((m_{x,y}))是个(s imes t)矩阵，N = ((n_{x,y}))是一个(p imes q)矩阵，(s in [s])是M的行指标，其定义域有一个自然的行次序。M(otimes)N是一个(sp imes tq)矩阵。

[M otimes N_{x,z;y,w} = m_{x;y}n_{z;w} ]

M(otimes)N有(stpq)个元素。M(otimes)N 以一定的次序和方式存储了MN的所有函数值。本质上，张量积就是以一定次序排序的函数乘积的函数表。

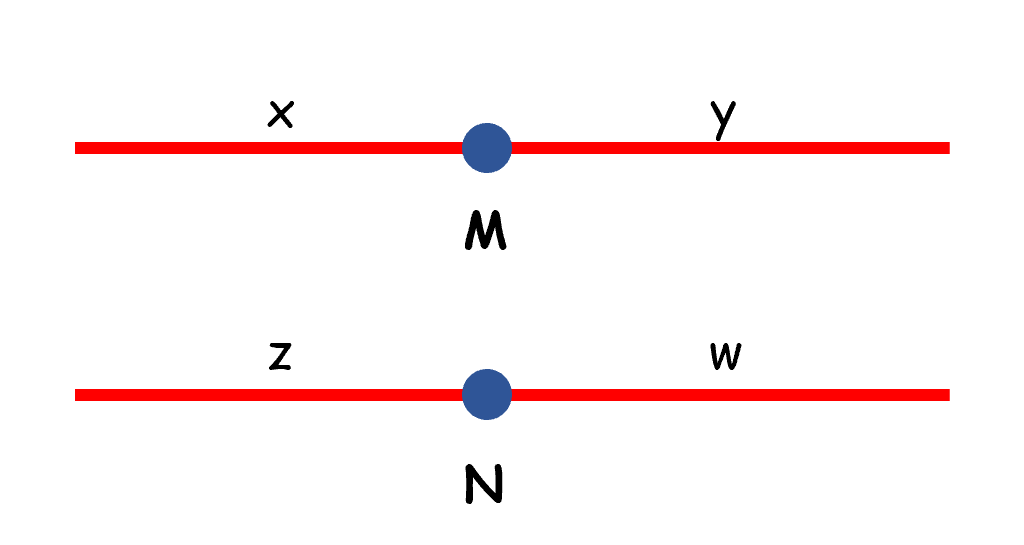
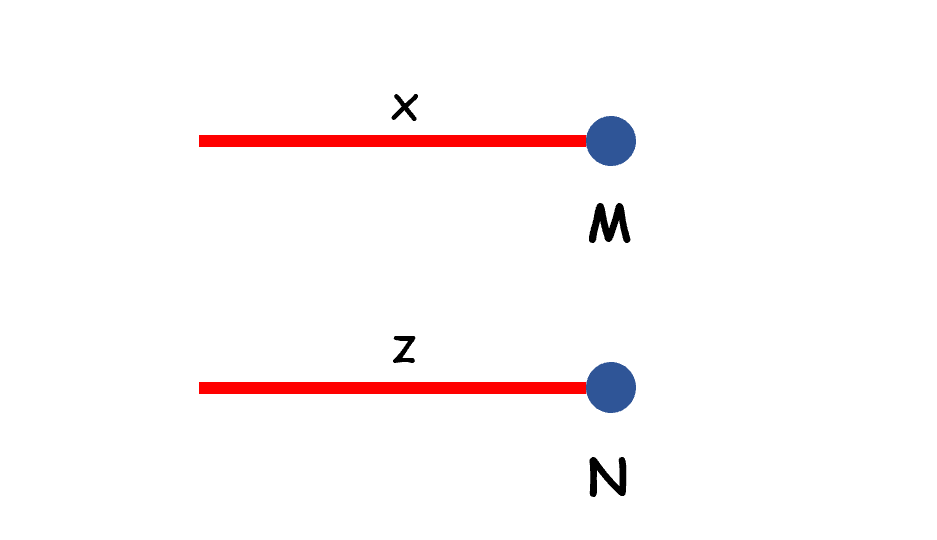
M和N也可以是单独的向量：

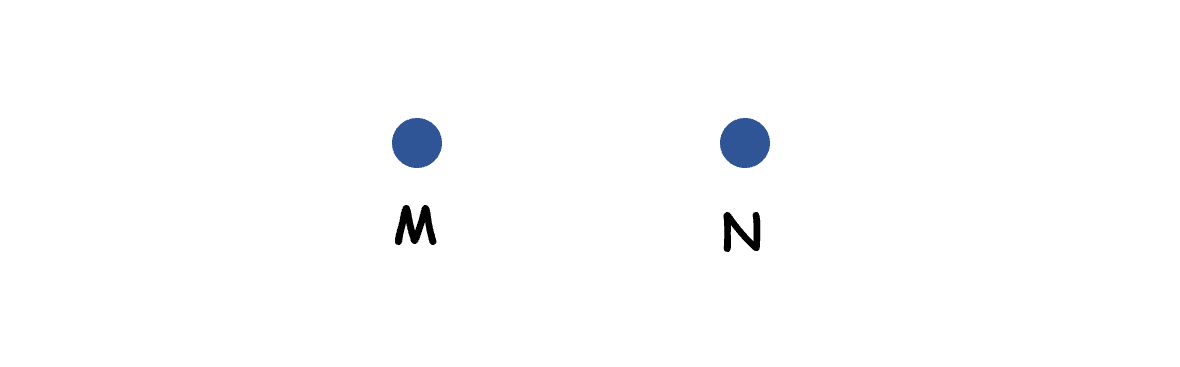
也可以没有边，只有顶点，即零元函数的张量积（(Motimes N = MN)）。

推论：一个无外部边的张量网络的值，是它各个联通分支的值的乘积。

推广：张量概念是矢量概念和矩阵概念的推广，标量是零阶张量，矢量是一阶张量，矩阵是二阶张量，而三阶张量则好比立体矩阵。用计算机的语言说，张量就是高维数组。张量网络是描述函数的结合的，其基本元素是函数，例如，一个(d)元函数(F:[k]^d ightarrow cal{C})

1.2.2、函数的矩阵形式

设(F)是一个(n+m)元布尔函数，可以任意把自变量区分为两部分，设(x_1,...,x_n,y_1,...y_m)是它的输入。对应(2^m imes 2^m)的矩阵(M = (M_{x_1,...,x_n,y_1,...y_m}))，其中

[M_{x_1,...,x_n,y_1,...y_m}= F(x_1,...,x_n,y_1,...y_m) ]

若取(m=0)(或(n=0))，就成了列（或行）向量。如下张量网络的函数可用（广义）矩阵乘法“((F_{x_1,x_2,y_1,y_2})(H_{y_1,y_2,z_1,z_2,z_3}))”表示：

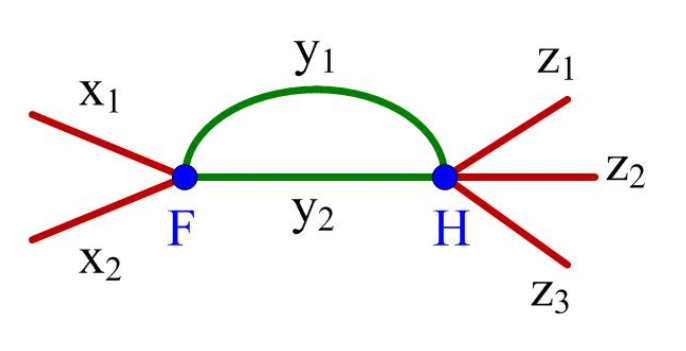
比如：((Acdot B)otimes(Ccdot D))和((Aotimes C)cdot (Botimes D))可以表示为：

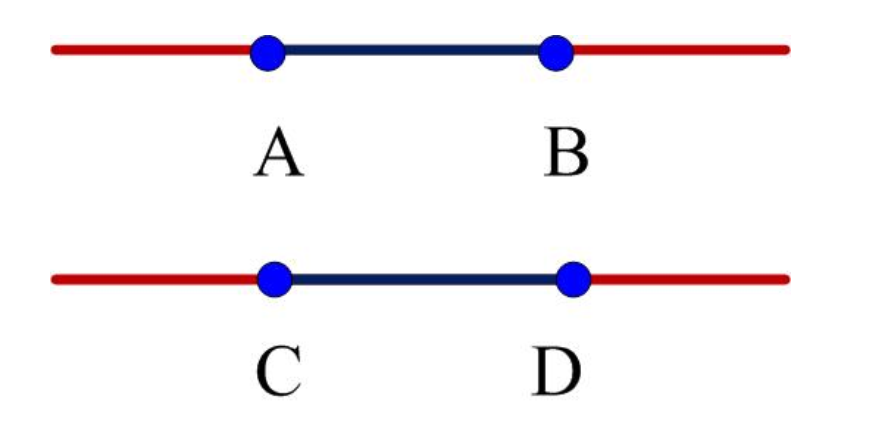
三、矩阵乘法与张量积的共同（同构）狭义情形

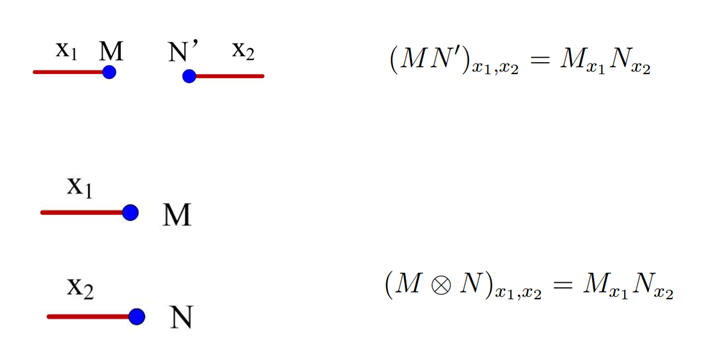
四、混合矩阵乘法与张量积

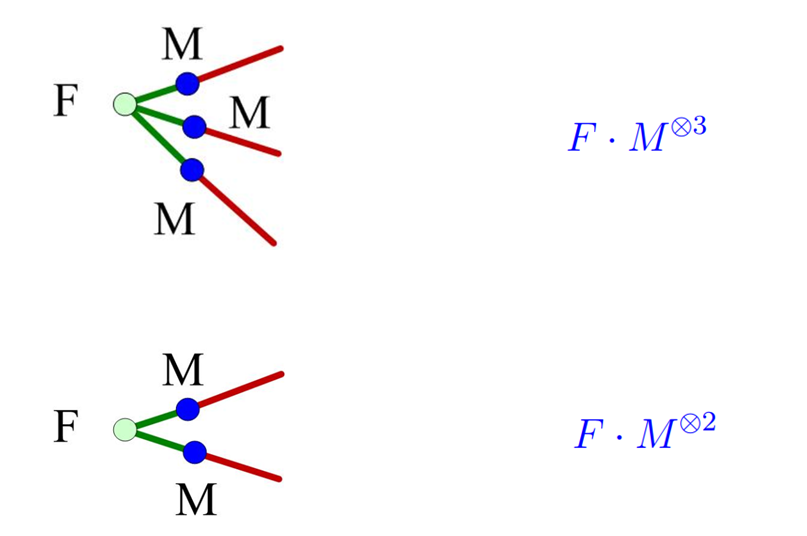
五、张量网络与迹

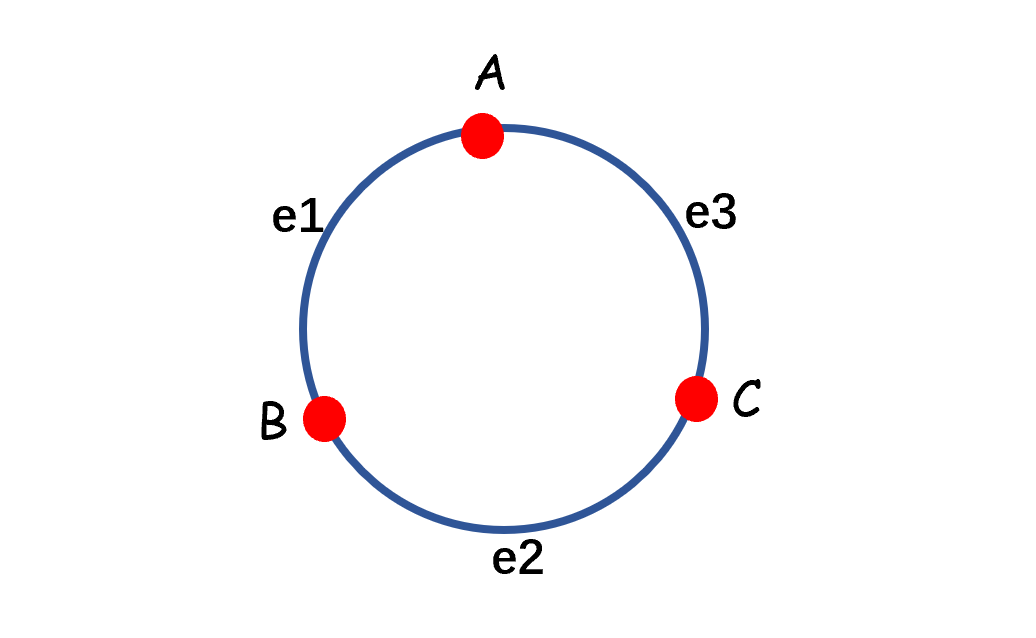
(trace(ABC) = sum_{e_1,e_2,e_3in [d]}A_{e_1e_3}B_{e_1e_2}C_{e_2e_3} = trace(BCA)=trace(C^{'}B^{'}A^{'}))