先说一个结论:有限域的阶为质数的幂。应用于密码学领域。
质数的幂: prime power
2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29, 31, 32, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 107, 109, 113, 121, 125, 127, 128, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 243, 251, 256, ...
有限域 finite field 又称伽罗华域;是一个定义了乘法,加法,减法和除法并满足基本规则的集合。 包含元素的个数称为阶,必为 prime power。
例子1:
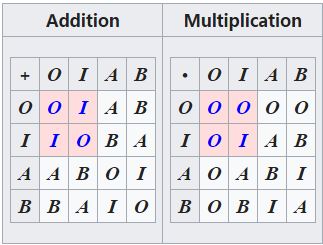
4个元素的有限域 GF(4)。
粉色部分为 binary field GF(2): O为假,I为真;加法为异或,乘法为‘ 且 ’ 。 coputing with bits 的结构。
例子2:对于集合 {0,1,2……,n-1}
当n为质数时,集合为有限域;
当 n 为合数时,可写为 n=s*r , 而按照集合上的乘法定义(取余数),s乘r 得到 0,sr=0, 我们假设 s 存在乘法逆元,两边乘上此逆元,得到r=0 的矛盾式。 说明,s 和 r 根本就没有逆元。所以此集合压根就不是域!
‘ 整数mod p, 当 p为质数’
复习一下: ‘ 整数模p ’ 是一个环,其元素为集合,即‘ 同余类’, 易证: 第一个集合为乘法的单位元; 第n个集合为加法的单位元。
有限域 Fd
我们假设其中元素 a0=0 为加法运算的单位元; a1=1 为乘法运算的单位元。
可以证明: 对于Fd 中任何元素 ai , 都有 a0ai = a0
首先,加法和乘法有运算结果(d=3):
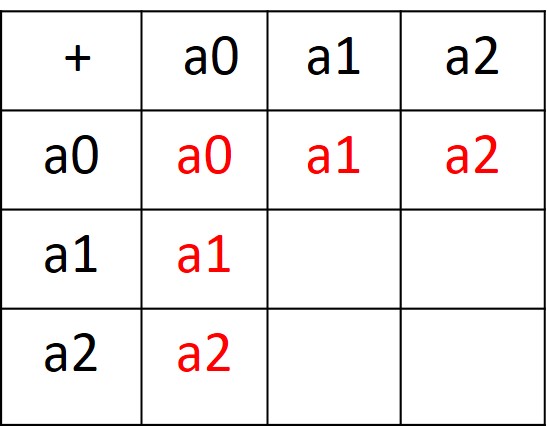
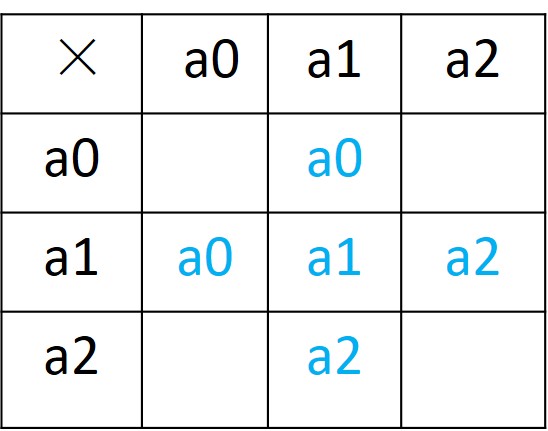
那么可得, a0=a0a1=a0(a0+a1)=a0a0+a0, 很显然: a0a0 只能为 a0
同理, a0+a2= a2= a1a2 =(a0+a1)(a2+a0) =a0a2+a2+ a0+a0= a0a2+a2, 等号两边加上 -a2 后得到: a0a2=a0
证明完毕。还可以进一步推导:
此外: 假设 a1+a2= a1, 右边加一个 a0, 则可得到 a2=a0, 矛盾。 所以只能是: a1+a2=a0
这样: a1+a1就不可能等于 a0, 只能等于 a2; a2+a2 也只能等于 a1
再根据乘法的逆元存在(对于非 a0),可得知 a2a2 只能为 a1.
如此: F3 运算表是唯一的。
充分利用‘ 域中元素均有加法逆元,且非 a0 元素均有乘法逆元’。可以证明:
1. 如果 ai*aj=a0, 那么其中至少有一个为 a0.
ai*aj+aj = aj
aj( ai+a1)=aj
假设 aj 不为 a0, 则等式两边乘上 aj 的逆元得到: ai+a1=a1=a1+a0 ; 再两边加上 a1 的逆元, 得到 ai=a0
证毕。
2. a0 乘上任何元素必为 a0
用反证法:假设 a0*ai=aj , aj 不为 a0;
分2种情况:若 ai 不为 a0, 那么两边乘上 ai 的逆元 ap,得到 a0=aj*ap, 由1可知 ap=a0, 但是域的定义中:a0 没有乘法逆元,也不会是其他元素的乘法逆元, 所以矛盾了;
若 ai 为 a0, 则 a0*a0 = aj, a0*a0+a0=aj, a0*(a0+a1)=aj, a0*a1=aj, 两边乘上 a1的逆元,矛盾!
证毕。
构造有限域的几种具体方式
1. 非质数域
即域的阶不为质数的1次方(不为质数本身)。构造 GF(q).
多项式的度 degree, 即最高次幂。
2. 对于有限域 GF(d), d=p^n, p为质数,n 为幂次。
利用‘ 有限有限域上的不可约多项式 ’ 的性质。 即考虑另一个有限域 GF(p) 为‘ 整数模 p ’ ={ 0,1,2…, p-1 }, 其上的一个多项式的一个根为 α ,
则 GF(d) 中的元素 a 可以展开为: a=a0*α0+a1*α1……+a(n-1)*αn-1 , 展开系数 a0,a1 属于 GF(p)
例如: p=3, n=2, 则 GF(3)={0,1,2}
其不可约多项式可以取为 x2+x+2=0, α 为其根。
则 GF(9) 的元素可以表示为: a0+a1*α1 系数 a0,a1 属于 GF(3)
总结: GF(d)中的元素 a 有 n 个展开系数,每个系数有 p个取值,所以一共有 d=p^n 个 a 元素.
3. 例子: 当 d=4 , p=2, n=2 时
在 GF(2)上只有一个度为2的不可约多项式: x2+x+1
a0+a1*α
故 GF(4) 的4个元素为: 0, 1,a, 1+a
4 例子 当 p>2, 且 n=2 时
先引入 ‘ 二次残余’ : quadratic residue
对于整数 q, 如果存在一个整数 x, 使得 x2 和 q 模 n 同余。
那么称 ‘ q 是模 n 二次残余的’。
现在对于 GF(p^2), 要找到 GF(p) 上的度为 2 的不可约多项式。 即为:x2 - r , r 为模 p 二次非残余。
如 p=3,5,11,13, …… r 可取 2
p=5,7,17, …… r 可取 3
a0+a1*α, 主要是借方程得到 α
5. GF(8) p=2, n=3 ; GF(27) p=3, n=3
x3 - x- 1 在 GF(2) 和 GF(3)上是不可约的。
6. GF(16) p=2, n=4
x4 + x+ 1 在 GF(2) 上是不可约的。