贝叶斯决策与学习
先验概率
先验概率 ( Prior probability)先验概率是在缺乏某个事实的情况下描述一个变量; 而后验概率是在考虑了一个事实之后的条件概率. 先验概率通常是经验丰富的专家的纯主观的估计. 比如在法国大选中女候选罗雅尔的支持率 p, 在进行民意调查之前, 可以先验概率来表达这个不确定性.
后验概率
后验概率 ( posterior probability) 后验概率可以根据通过Bayes定理, 用先验概率和似然函数计算出来。
后验概率是基于新的信息,修正原来的先验概率后所获得的更接近实际情况的概率估计。
举一个简单的例子:一口袋里有3只红球、2只白球,采用不放回方式摸取,求:⑴ 第一次摸到红球(记作A)的概率;⑵ 第二次摸到红球(记作B)的概率;⑶ 已知第二次摸到了红球,求第一次摸到的是红球的概率。解:⑴ P(A)=3/5,这就是验前概率;⑵ P(B)=P(A)P(B|A)+P(A逆)P(B|A逆)=3/5⑶ P(A|B)=P(A)P(B|A)/P(B)=1/2,这就是验后概率。
后验概率公式

贝叶斯决策的一般过程
(1)估计先验概率:①根据实际情况做经验估计;②根据样本分布的频率估计概率。
(2)计算类条件概率密度:①参数估计:类条件概率分布类型已知,参数未知,通过训练样本来估计(最大似然法、Bayes估计);②非参数估计:不判断类条件概率分布类型,直接根据训练样本来估计。
(3)计算后验概率。
(4)若进行最小错误率决策,根据后验概率即可作出决策。若进行最小风险决策,按照下式计算即可。

MAP分类器
最大后验概率分类器:将测试样本决策分类给后验概率最大的类
判别公式

决策边界
对于MAP分类器来说,决策边界位于

单位空间通常有两条决策边界,高维空间:复杂的非线性边界

MAP分类器决策误差
给定一个样本x,MAP分类器决策产生的误差可以用概率误差表达
概率误差等于未选择的类所对应的后验概率

所有样本分类决策产生的平均误差为

MAP分类器决策目标:最小化概率误差,即分类误差最小化
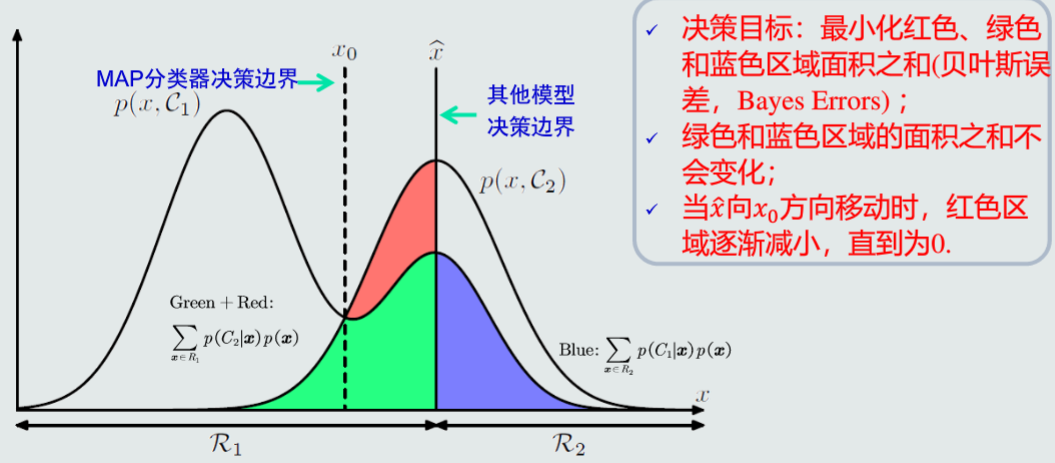
高斯观测概率
观测概率:单维高斯分布,其分布函数为:

将高斯分布函数带入MAP判别公式

两边同时取对数,可以得到

为得到决策边界,使式子两边相等 得


分类器决策偏向先验概率高的类,和MICD分类器比较MAP分类器偏向方差较小的类
决策风险与贝叶斯分类器
决策风险得评估
给定一个样本x,分类器决策其属于Ci类的动作αi对应的决策风险可以定义为相对于所有候选类别的期望损失。记作

贝叶斯分类器
在MAP分类器的基础上,加入决策风险因素,得到贝叶斯分类器
给定一个样本x,贝叶斯分类器选择决策风险较小的类。
决策损失
给定单个测试样本,贝叶斯决策损失就是决策 风险
给定所有测试样本,贝叶斯决策的期望损失:多有的决策损失之和

决策目标
给定所有样本,贝叶斯分类器的决策目标是最小化期望损失,即对每个测试样本选择风险最小的类

朴素贝叶斯分类器
假设特征之间是相互独立的,则有
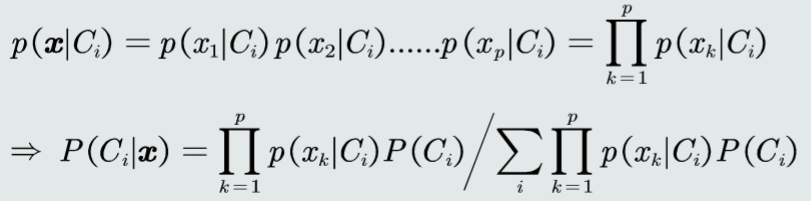
常用的参数估计方法
极大似然估计
最大似然估计的目的是利用已知的样本结果,反推最有可能导致这样参数值。
似然函数
联合概率密度函数P(D|θ)称为相对于{x1,x2,...,xn} θ 的似然函数
l(θ)=P(D|θ)= P(x1,x2,x3,...,xn|θ)=p(x1|θ)p(x2|θ).....*p(xn|θ)
如果 θ'是参数空间中可能使似然函数l(θ)的最大 θ 指则 θ'应该是”最可能“的参数值,那么 θ'就是 θ 的极大似然估计量。是样本集的函数,记作
θ^=d(x1,x2,....,xn)=d(D)
θ^(x1,x2,x3,...,xn)称作极大似然函数估计值
求解极大似然函数
ML估计,求使得出现该组样本的概率最大的 θ 值
θ^=argmax l(θ)=argmax p(x1|θ)*p(x2|θ)*.....*p(xn|θ)
为了方便分析,定义了对数似然函数
H(θ)=ln(θ)
θ^=argmax ln p(x1|θ)*ln p(x2|θ)*.....*ln p(xn|θ)
当未知参数只有一个(θ为标量)时
在似然函数满足连续,可微正则条件下,极大似然估计量是下面微分方程的解:
dl(θ)/dθ=0 或 dln(θ)/dθ=0
当未知参数有多个时(θ为向量)时
则θ可表示为具有S个分量的未知向量 θ=[θ1,θ2,....θs]T
记梯度算子
▽θ=[∂/∂θ1,∂/∂θ2,....∂/∂θn]T
若似然函数满足连续可导的条件,则最大似然函数估计量就是如下方程的解
▽θln(θ)=Pθln p(x1|θ)ln p(x2|θ).....ln p(xn|θ)=0
例题
为了方便理解,我先用课上的例题作为例子。
例题如下


过程就是先写出概率函数,再取对数,再求导,再解方程。
贝叶斯估计
已知样本满足某种概率分布,但参数未知。贝叶斯估计把待估参数看成符合某种先验概率分布的随机变量。对样本进行观测的过程就是把先验概率密度转化为后验概率密度,这样就利用样本信息修正了对参数的初始估计值。
贝叶斯定理
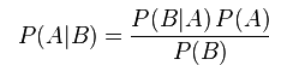
在参数估计中可以写成

贝叶斯估计是在MAP上做进一步拓展,此时不直接估计参数的值,而是允许参数服从一定概率分布。极大似然估计和极大后验概率估计,都求出了参数的值,而贝叶斯估计则不是,贝叶斯估计扩展了极大后验概率估计MAP(一个是等于,一个是约等于)方法,它根据参数的先验分布和一系列观察,求出参数的后验分布,然后求出的期望值,作为其最终值。另外还定义了参数的一个方差量,来评估参数估计的准确程度。
贝叶斯算法过程

贝叶斯估计和极大似然估计的区别
最大似然估计和贝叶斯估计最大区别便在于估计的参数不同,极大似然估计要估计的参数θ被当作是固定形式的一个未知变量而贝叶斯估计则是将参数视为是有某种已知先验分布的随机变量,意思便是这个参数他不是一个固定的未知数,而是符合一定先验分布如:随机变量θ符合正态分布等,那么在贝叶斯估计中除了类条件概率密度p(x|w)符合一定的先验分布,参数θ也符合一定的先验分布。我们通过贝叶斯规则将参数的先验分布转化成后验分布进行求解
在算法的复杂性上,贝叶斯估计要比极大似然估计来的复杂,而当采用的样本数据很有限时,贝叶斯估计误差更小。
KNN估计
k近邻是利用训练数据对特征特征空间进行划分,并作为其分类的模型。k近邻三要素:
k值的选择
k值大,意味着模型简单。也就是说数据点在离聚类中心很远的时候,依旧可以归类。这样一来,近似误差会变大,不那么相似的数据点也会被归类。
k值小,意味着模型复杂。也就是说只有离聚类中心很近,才可以归类。这样一来,估计误差会变大,如果周围出现噪声,预测会出错。
k值一般会选取一个较小的值,然后利用交叉验证集进行选取最优的k值。
距离度量

曼哈顿距离p=1

欧式距离p=2
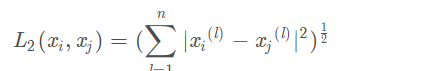
p=无穷大(计算出各个维度的绝对值之后,取其中的最大值)

分类决策规则
多数表决:数据中的多数决定最后的类。
这种表决方法满足经验风险最小化,p(非x)=1-p(x),如果p(非x)代表错分类的概率,那么使得其最小即p(x)最大,也就是多数决策。

优缺点
优点:可以自适应的确定x相关的域R的范围。
缺点:
KNN估计不是连续函数
不是真正的概率密度表达
直方图和核密度估计
直方图估计
手动将特征空间划分成若干个区域,待估计模型只能分配到对应的固定区域,缺乏自适应能力

优缺点
优点:
固定区域R:减少由于噪声产生的估计误差
不需要存储样本
缺点:
固定区域R的位置:如果模式x落在相邻格子的交界区域,意味着当前格子不是以模式x为中心,导致统计与概率估计不准确。
固定区域R的大小:缺乏概率估计的自适应能力,导致过于尖锐或平滑
核密度估计
所谓核密度估计,就是采用平滑的峰值函数(“核”)来拟合观察到的数据点,从而对真实的概率分布曲线进行模拟。
原理

核密度估计(Kernel density estimation),是一种用于估计概率密度函数的非参数方法,为独立同分布F的n个样本点,设其概率密度函数为f,核密度估计为以下:

h>0为一个平滑参数,称作带宽(bandwidth),也看到有人叫窗口。
Kh(x) = 1/h K(x/h). 为缩放核函数(scaled Kernel)。
核密度函数的原理比较简单,在我们知道某一事物的概率分布的情况下,如果某一个数在观察中出现了,我们可以认为这个数的概率密度很大,和这个数比较近的数的概率密度也会比较大,而那些离这个数远的数的概率密度会比较小。
基于这种想法,针对观察中的第一个数,我们可以用K去拟合我们想象中的那个远小近大概率密度。对每一个观察数拟合出的多个概率密度分布函数,取平均。如果某些数是比较重要的,则可以取加权平均。需要说明的一点是,核密度的估计并不是找到真正的分布函数。
优缺点
优点:
一代估计模式x为中心,自适应确定区域R的位置
使用所有训练样本,而不是根据第K个邻近点来估计概率密度,从而克服KNN估计存在的噪声影响
如果核函数是连续,则估计概率密度的函数也是连续
缺点:
与直方图估计相比,核密度估计不提前根据训练样本估计每个格子的统计值,所以它必须存储所有的训练样本
核密度估计与直方图估计
核密度估计比直方图估计更加平滑
