一、线性最小二乘拟合
使用一个简单函数在整体上逼近已知函数,使其在整体上尽可能与原始数据曲线近似。记为:
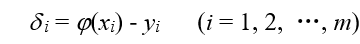
称之为拟合曲线 ,若该函数为插值多项式,则所有偏差为零。
,若该函数为插值多项式,则所有偏差为零。
但实际情况中,我们不可能要求近似曲线
y = 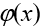
严格通过这么多数据点。但为了使其尽可能反映所给数据的变化趋势,我们可以要求偏差的绝对值尽可能小,甚至是所有偏差中的最大值尽可能小。我们可以通过使选取的近似曲线在节点xi 处的偏差的平方和达到最小来实现这一目标,这一原则就是 最小二乘原则。
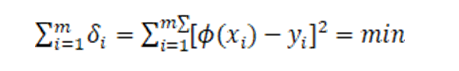
按最小原则选择的拟合曲线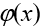 就称为最小二乘拟合曲线,此方法称为最小二乘法。
就称为最小二乘拟合曲线,此方法称为最小二乘法。
实用公式推导:
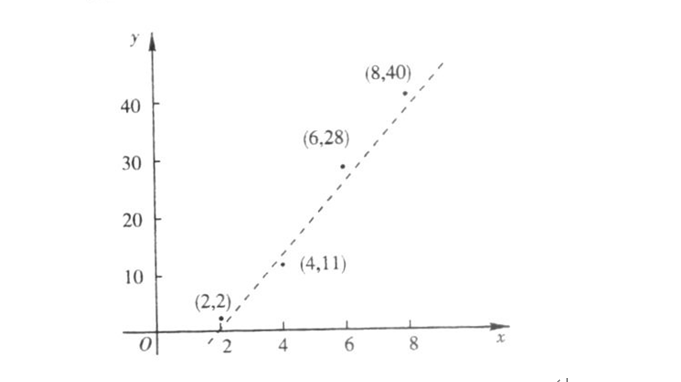
假设我们此处有这样一组数据点,这些点的分布接近于在一条直线上,因此选一条直线(一条曲线则加入对应方程推导)来拟合这组数据,令:
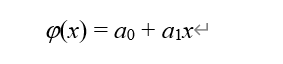
根据最小二乘原则,有:
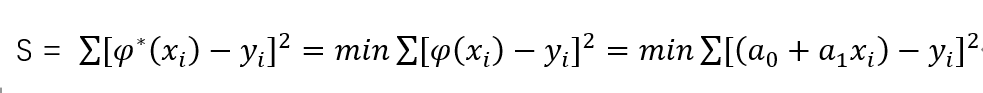
令a0,a1为未知数,则此处转换为求二元函数S(a0,a1)的极小点问题:
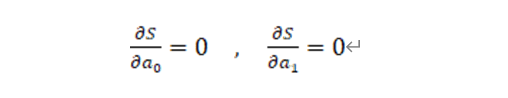
由此可得:

联立解得:
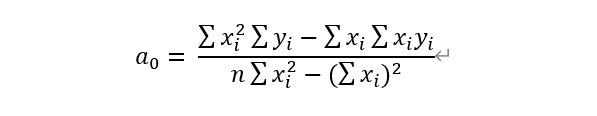
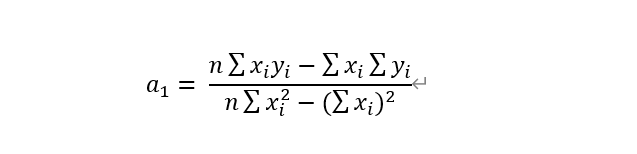
即得到了待求的拟合直线段。
C++实现:
bool gFittingLine(double *xArray, double *yArray, int firstIndex, int lastIndex,
double &a, double &b)
{
int count = lastIndex-firstIndex+1;
if(count < 2) return false;
double s0 = (double)count, s1 = 0, s2 = 0, t0 = 0, t1 = 0;
for(int i=firstIndex;i<=lastIndex;i++)
{
s1 += xArray[i];
s2 += (xArray[i]*xArray[i]);
t0 += yArray[i];
t1 += (xArray[i]*yArray[i]);
}
double d = s0*s2-s1*s1;
b = (s2*t0-s1*t1)/d;
a = (s0*t1-s1*t0)/d;
return true;
}
实现对二维平面离散点的曲线拟合
二、最小二乘面拟合
对空间中的一系列散点,寻求一个近似平面,与线性最小二乘一样,只是变换了拟合方程:
使用平面的一般方程:
Ax + By + CZ + D = 0
可以令平面方程为:

由最小二乘法知: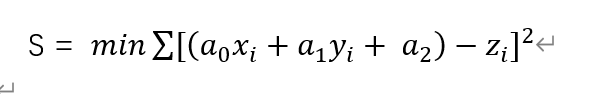
同样分别取 a0,a1,a2的偏导数:

即是:
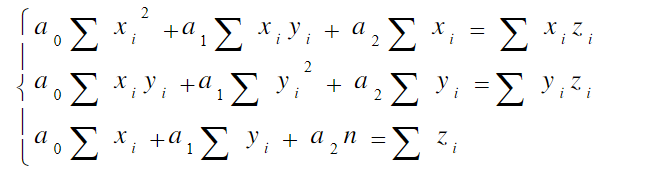
换算为矩阵形式有:
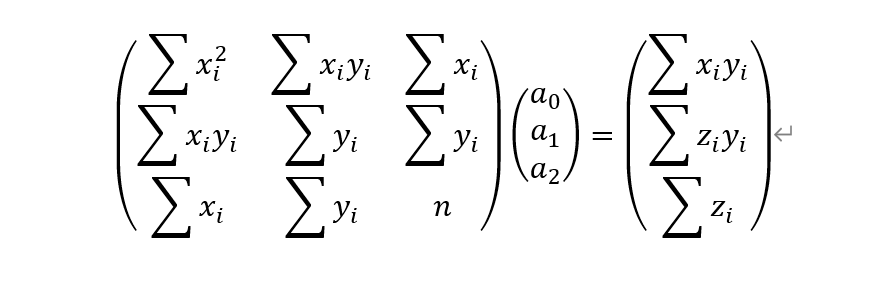
可以直接通过克拉默法则求出a0,a1,a2的行列式表达式,有:
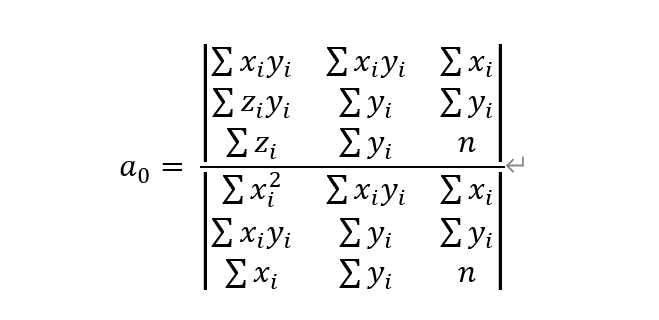

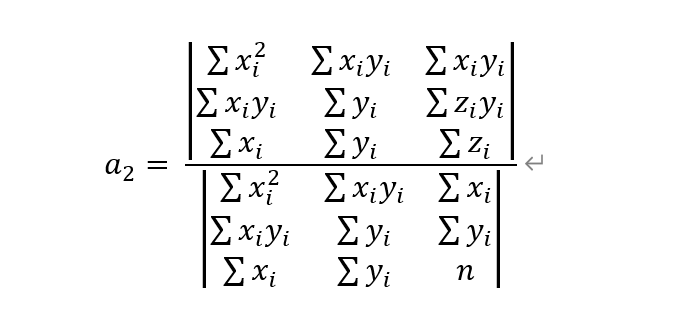
c++实现(gDaterm3() 为自定义的三阶行列式计算函数):
bool gFittingPlane(double *x, double *y, double *z, int n, double &a, double &b, double &c)
{
int i;
double x1, x2, y1, y2, z1, xz, yz, xy, r;
x1 = x2 = y1 = y2 = z1 = xz = yz = xy = 0;
for(i=0; i<n; i++)
{
x1 += x[i];
x2 += x[i]*x[i];
xz += x[i]*z[i];
y1 += y[i];
y2 += y[i]*y[i];
yz += y[i]*z[i];
z1 += z[i];
xy += x[i]*y[i];
}
r = gDeterm3(x2, xy, x1, xy, y2, y1, x1, y1, n);
if(IS_ZERO(r)) return false;
a = gDeterm3(xz, xy, x1, yz, y2, y1, z1, y1, n) / r;
b = gDeterm3(x2, xz, x1, xy, yz, y1, x1, z1, n) / r;
c = gDeterm3(x2, xy, xz, xy, y2, yz, x1, y1, z1) / r;
return true;
}