参考资料
看到期望经过次数的说法:https://blog.csdn.net/bzjr_Log_x/article/details/100007360
你谷题解:https://www.luogu.com.cn/blog/Kelin/solution-p3706
期望经过次数和概率在无向图之间的联系
是不是看到这个头都要爆炸了。
前言
也许许多时候你总是会看到一些题目,问你最终概率,但是其转移过程是无向图的,这个时候,高斯消元大爷肯定是不二之选。(至少我现在还没有看到哪个无向图概率题是不用高斯消元的)
正片
现在给你一个这样的无向图:
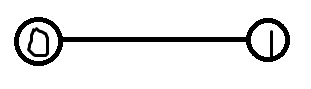
我们从(0)号点出发,走到(1)的概率是多少(走到(1)就停),(50\%)停留在原地,也许你会直接说,这不就是(1)吗。
但是如果要你列出概率方程,额。。。。
设(f[i])为到达这个点的概率,然后(f[1]=frac{1}{2}f[0])?
但是(f[0])的概率为(0),总么可能转移的了啊。
这个时候,我们终于发现了一个事情,因为概率这个东西更加反映的是结果,即各个随机事件之间所发生样本个数和总样本个数间的比例,其对于中间过程十分不友好,因为中间过程也许根本连样本个数都没有。
于是统计其概率就成了一个十分玄乎的事情。不就是1吗
事实上,当然对于这个图也存在微积分的方法,但是当点数很多,终点很多,微积分也许就不是一个好主意了。
但是,这个时候,我们引入一个新的东西,点的期望经过次数,这个就对于中间点十分的友好,因为其中间点也可以有确定的数值,那么如何统计呢?对于一个点(x),如果存在一条路径可以到(x)(假设这个时候突然停下来等一等,毕竟(x)不是终点,后面还会继续跑),那么就把这条路径现在的概率乘(1)加到(e[x])中((e[x])表示期望经过次数),当然,一条路径可能经过(x)多次,因此当一条路径经过(x)时,其可能已经经过(x)好几次了。
当然,这也是个无限的东西,他是否是收敛的,我并不会证,但是用高斯消元一样可以求得,后面会讲。
最神奇的一件事情是,(e[ed])就等于(ed)的概率。((ed)可能有多个)
仔细观察就会发现,(e[ed])的定义刚好就是(ed)的概率的定义(或者说是经典求法),此时我们前文括号里说停下来等一等就是永远停下来了,因为到了(ed)就停下来。
发现了这个美妙的性质,无向图的概率题基本上都可以用期望经过次数来搞了。
无向图的期望问题
本文无法保证正确性
事实上,期望无非是列个式子,高斯消元。
期望经过次数
本文先讲如何求期望经过次数。
需要严重注意的事情是:实际上,期望的转移过程不能但看几个变量间存在概率关系就直接乘上概率转移,因为期望在无向图上之所以有最终答案是因为无限是可以通过求极限得到确值的,比如:期望次数,其只是一坨式子的结果,你不能单单把这个当成次数来耍除非你是老手。在后文,就会举一个错误示范。当然,许多用法都是可以证明是对的,比如下文提到的把边的期望经过次数转换为两端点的期望经过次数。
好,扯了这么多,关键是次数怎么求你是一句话也没讲啊。这不就来讲了吗。
首先,设(E(x))为到(x)的期望经过次数,(Edge)为边集,(p(x,y))为经过这条边的概率(当然,有时候(x,y)走这条边的概率可能不相同,因此(p(x,y)≠p(y,x))),那么(E(y)=sumlimits_{(x,y)∈Edge,x≠ed}E(x)p(x,y))。
现在证明在期望具体式子中也是对的。
设存在一条从起点到(x)并且停下来一下的路径(T),其目前的概率为(S),然后其转移到(y)的概率为(p(x,y)),那么显然(T+y)(就是路径又多了个(y))的概率就是(S*p(x,y)),因为(T)不重复,所以(T+y)也不重复,概率就是所有加起来,也就是(E(x)*p(x,y))。
但是,比较特殊的,(E(1)+=1),因为从起点出发,必须经过。
而这个统计期望经过次数的,在我的另外一篇期望博客有进行实践。应该
期望经过长度
这种题目一般就是边还有长度,求到达终点的期望经过长度。
这个一般就两种求法,一种是边的期望经过次数,可以转换为两端点的期望经过次数,还有一种是直接霸王硬上弓。
第一种不讲了。
第二种我们考虑像期望经过次数一样,设(f(x))表示从起点到达(f(x))的期望长度。
那么(f(y)=sumlimits_{(x,y)∈Edge,x≠ed}(f(x)+w(x,y))p(x,y)=sumlimits_{(x,y)∈Edge,x≠ed}f(x)p(x,y)+w(x,y)p(x,y))((w)为边权)。
但是从期望的角度来看,这是错的。
这里假设边权都是(1),也就是(f(y)=sumlimits_{(x,y)∈Edge,x≠ed}f(x)p(x,y)+p(x,y))。
存在(st->x)的路径(T),以及其概率(S),还有其价值(V)。
那么理论上:(T+y)的(S',V')为(S*p(x,y))和(V+1)。
根据期望化一下式子:(S*p(x,y)*(V+1)=S*p(x,y)*V+S*p(x,y)),而我们发现,(f(x)*p(x,y))其实就是(S*p(x,y)*V)。
但是(S*p(x,y))嘛,根据乘法分配律:(p(x,y)sumlimits_{所有st->x的路径} S_{每条路径的概率}),然后我们发现,这后面不就是(E(x))吗,但是呢,我们的统计方法是(p(x,y)),其实换成(E(x))应该(没有实践过)就是对的,但是(p(x,y))绝对错。(事实上,你可以发现,如果边权全部为(0),初始(V)为(1),这其实就是求期望经过次数)
因此,期望的东西不能光凭感觉行事实际上屑作者也没有实践过,如果你不是搞期望的老司机,最好不要在没有根据的情况乱搞式子。
但是,如果我们设(f(x))为到达(ed)的期望长度,以(f(st))为答案的话,那么,式子就变成了:(f(x)=sumlimits_{(x,y)∈Edge}(f(y)+w(x,y))p(x,y)=sumlimits_{(x,y)∈Edge}f(y)p(x,y)+w(x,y)p(x,y)),其中(f(ed)=0)。
那么这个是不是对的呢?
存在(y->ed)的路径(T),以及其概率(S),还有其价值(V)。
那么理论上:(x+T)的(S',V')为(S*p(x,y))和(V+w(x,y))。
根据期望化一下式子:(S*p(x,y)*(V+w(x,y))=S*p(x,y)*V+S*p(x,y)*w(x,y)),而我们发现,(f(x)*p(x,y))其实还是(S*V*p(x,y)),但是(S*p(x,y)*w(x,y)),把所有路径的(S)加起来,它等于多少呢?不难发现,这个总和其实就是从(y)到达(ed)的概率,显然根据洛必达法则其实就是显然,因为到(ed)才停,所以最后一定会到达(ed),所以概率为(1),所以最终和为(p(x,y)*w(x,y)),WOC,真的对了。
从此不难看出,因为从(ed)往(st)推起的期望有一个很重要的性质,就是每个点到(ed)的概率都为(1),所以在做期望的时候,如果到(ed)就停,可以优先考虑从(ed)推起,思维难度可能会比较小应该吧。
其他的无向图期望自己推吧,这里只是讲讲期望概率的误区,以及一种比较直观的理解方法。
[SDOI2017]硬币游戏
题目
做法
事实上,这个只是帮助理解概率的应用问题的。
TLE做法
如果你对无向图期望认识比较浅,建议去多受点题目的折磨,简称刷题
这道题目求概率,尝试从期望经过次数入手。
首先,建立(AC)机。
对于(x)节点的两个儿子(这里(AC)机用了儿子优化,即如果一个点没有这个儿子,会自动填入(fail)的儿子到这个儿子位置)建立期望转移方程(其实就是单源多汇求期望经过次数),由于用了优化的(AC)机(这里必须要用了优化的(AC)机,因为每个点必须要有两个儿子。),所以是有向有环图(可能无环),处理起来其实跟无向图没什么区别,处理方法就不赘述了,因此节点个数为(nm),时间复杂度:(O((nm)^3)),只能过(4)个点。
但是这里其实有个优化,理论能过(70)分,就是因为每个点只会出现在两条方程,不难发现,在消掉第(i)项时,第(i)个方程到第(n)个方程中每个点也最多只会出现在两条方程中,于是可以优化到(O((nm)^2)),可以过(7)个点吧,应该。
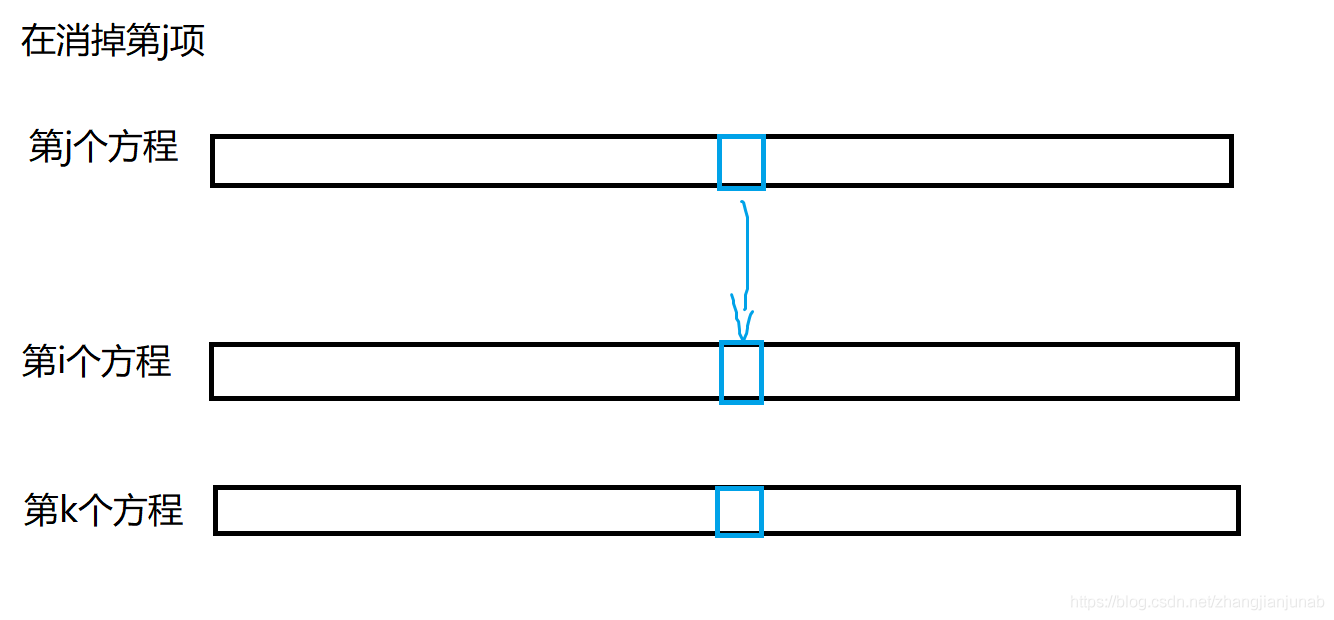
证明:根据数学归纳法,假设第(j)个方程到第(n)个方程之间每个点最多只出现了两次(也就是只有两条方程中这个点的系数不为(0)),那么在消掉第(j)项时,因为每个点最多只出现两次,所以第(j)个方程只与第(i)个方程进行消元,蓝框框就表示点系数的转移,不难发现,第(j+1)个方程到第(n)个方程,蓝框框依旧最多两个,由于一开始就满足假设,归纳法证毕。
优化
其实不能叫优化,已经是全新做法了。
甚至和(AC)机也没啥关系。
因为发现,在(AC)机中,除了(ed)以外,其余的点我们根本就不需要他们的期望经过次数,考虑合多为(1),化成(n+1)条方程。
现在约定:(A+B),就是把(B)串放到(A)串后面形成的串,模式串就是那群人猜的串,(f(X))表示出现(X)模式串的概率,实际也就是包含(X)的串的期望经过次数。
现在用(0/1)串代替(TH),显然,一个长度为(n)且不含任何模式串的串出现概率为(frac{1}{2^n}),实际上也就是期望出现次数(因为,在串后面加(0/1)的期望经过次数转移可以写成二叉树来转移,一个点的期望经过次数为其父亲的(frac{1}{2}),第(n)层表示长度为(n)的串,而一个点的期望等于其左右儿子的期望之和)。
有人说,但是不是有(ed)吗,但是你考虑一下,如果到了(ed)继续跑,那么概率是不是(frac{1}{2^n}),只不过到了(ed)继续跑的串我们不去问他的概率,而且对于一个串(N+A)((N+A)的串只在最后含(A),且(N)不含任何模式串,(A)为模式串),设后面的串为(T),(N+A+T)的长度为(n),我们把(N+A+T)的概率全部加起来,很明显就是等于(N+A)的概率,所以这样变形,概率也并不会变,只是帮助证明罢了。
现在设不含任何模式串的串的集合为(S)(空串当然也包含在内),当然,下文为了方便,直接用(S)表示(S)的元素,(f(S))表示(S)集合中所有元素的期望出现次数,(|S|)为(S)元素的长度。
考虑寻找(S)和每个模式串的关系。
对于任意一个包含(A)的串,实际就是用(S+A)拼接而成的,而且所有的包含(A)的串都可以这样表示。
但是是不是意味着(f(X)=frac{1}{2^m}f(S)),错!!!
比如(A=01,B=00)。
(S+A=S+01)
但是如果(S=S'+0),那么(S+A=S'+001=S'+B+1),这样(B)不就出现过了吗,所以(f(B))也就有可能惨一脚,所以就变成了(f(X)+???=frac{1}{2^m}f(S))。
但是这惨一JO的程度有多大呢?
这里证明,如果(A)长度为(a)的前缀等于(B)长度为(a)的后缀,那么(f(B))惨一脚的程度为(f(B)*frac{1}{2^{m-a}})。
设(S=S'+B长度为a的前缀),(T)为(A)长度为(a)的后缀。
为什么(S'+B+T)中(B)惨一脚的程度为(f(B)*frac{1}{2^{m-a}})。
实际上,你有没有考虑过(S'+B)最先出现的也不是(B),但是鉴于(S)中不含任何模式串,所以,(S'+B)中先出了(C)串,而(B)的前缀等于(C)的后缀,那么(C)的最后一个字符一定出现在(S+A)的(A)串区间中,所以(C)的后缀也等于(B)的前缀,在统计(C)时会被统计到。
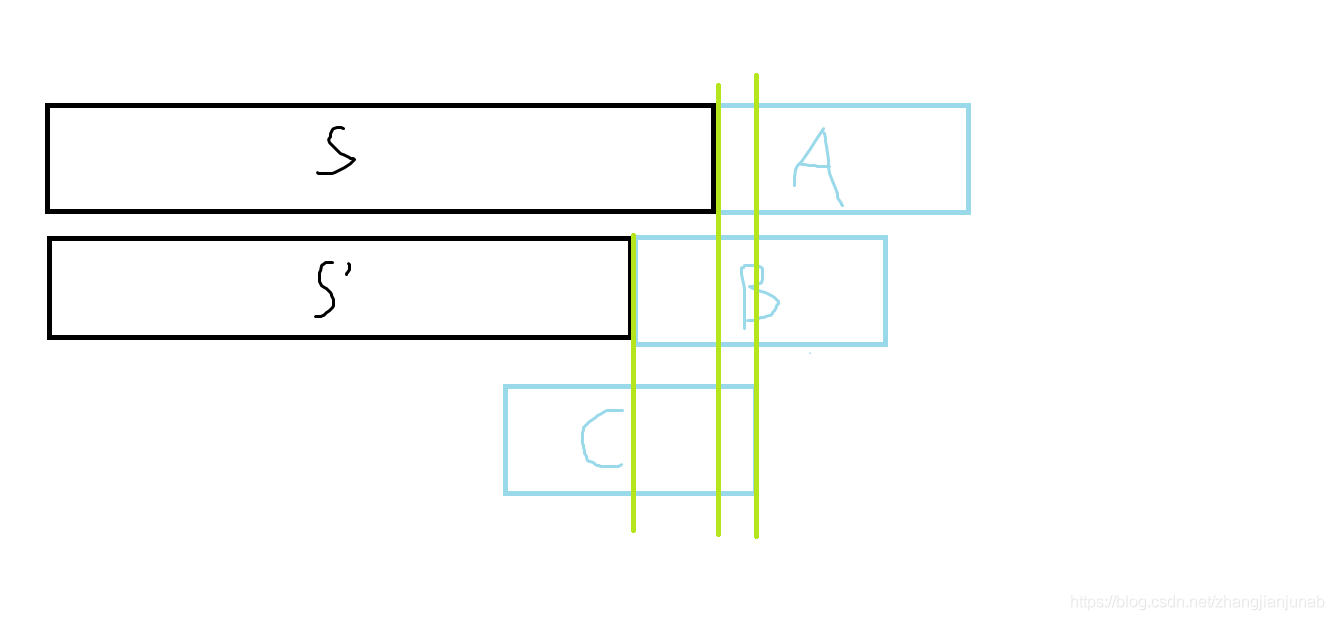
所以,(f(B)*frac{1}{2^{m-a}})实际上加上的时(S'+B)中(B)时唯一模式串的情况,也就是(f(B)),但是为什么要乘(frac{1}{2^{m-a}}),废话,一个长度为(|S|+m),一个长度为(|S'|+m),具有可比性吗,我们的目的是为了把掺一脚的程度加上,使其不再(f(A))中统计,而不是单纯的把(f(B))加上,自然需要乘(frac{1}{2^{m-a}}),串的表现就是(S'+B+T)才等于(S+A),树的表现就是要让(S'+B)所在点的位置等于(S+A)的位置(乘(frac{1}{2^{m-a}})让层数相同,((S+A))一定在((S'+B))的子树内)。
当然,一个字符串是可以多掺几脚的,谁说(A)前缀等于(B)后缀的(a)只能有一个。
公式则为:(f(A)+sumlimits_{B是模式串}sumlimits_{a=1}^m[A长度为)a(的前缀等于)B(长度为)a(的后缀]f(B)*frac{1}{2^{m-a}}=f(S)*frac{1}{2^m})(其中([x])为(x)成立,([x]=1),不成立,([x]=0))
当然,这里只有(n)条公式,我们发现所有的模式串的概率加起来为(1),所以就是(sumlimits_{A是模式串}f(A)=1)。
这样就有(n+1)条方程了。
匹配前缀后缀后Hash。
时间复杂度:(O(n^3))。
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 310
using namespace std;
typedef long long LL;
template<class T>
inline T zabs(T x){return x>=0?x:-x;}
char st[N][N];
LL has[N][N],ta=235,tb=1e9+7,fc[N];
inline LL find_hash(LL *ha,int l,int r){return (ha[r]-(ha[l-1]*fc[r-l+1])%tb+tb)%tb;}
int n,m;
long double erfen[N];
long double f[N][N],ans[N];
void GSXY()
{
n++;
for(int i=1;i<=n;i++)
{
int id=i;
for(int j=i+1;j<=n;j++)
{
if(zabs(f[j][i])>zabs(f[id][i]))id=j;
}
if(id!=i)swap(f[id],f[i]);
for(int j=i+1;j<=n;j++)
{
double bili=f[j][i]/f[i][i];
for(int k=n+1;k>=i;k--)f[j][k]-=f[i][k]*bili;
}
}
for(int i=n;i>=1;i--)
{
ans[i]=f[i][n+1]/f[i][i];
for(int j=i-1;j>=1;j--)f[j][n+1]-=ans[i]*f[j][i];
}
n--;
}
int main()
{
scanf("%d%d",&n,&m);
fc[0]=1;for(int i=1;i<=m;i++)fc[i]=fc[i-1]*ta%tb;
erfen[0]=1;for(int i=1;i<=m;i++)erfen[i]=erfen[i-1]*0.5;
for(int i=1;i<=n;i++)scanf("%s",st[i]+1);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)has[i][j]=(has[i][j-1]*ta+st[i][j]-'A'+1)%tb/*这里如果不加1,可能会使代码很难辨析AAB和AB*/;
}
for(int i=1;i<=n;i++)
{
f[i][n+1]=-erfen[m];
for(int j=1;j<=n;j++)
{
for(int k=1;k<=m;k++)
{
if(find_hash(has[j],m-k+1,m)==find_hash(has[i],1,k))f[i][j]+=erfen[m-k];
}
}
}
f[n+1][n+2]=1;for(int i=1;i<=n;i++)f[n+1][i]=1;
GSXY();
for(int i=1;i<=n;i++)printf("%Lf
",ans[i]);
return 0;
}
小结
概率期望真美妙。