傅里叶变换在多项式乘法中的应用（一）

(A(x) = a_0 + a_1 x + a_2 x^2 + ··· + a_{n-1} x^{n-1})

求多项式的点值表达式

为了得到(A(x))的点值表达式，选择一些比较特殊的(x:=w_n^k)，(k in {0,1,2,···,n-1})代入。

已知(e^{i heta} = cos heta + i sin heta)

记 (w_n^k = e^{i*(frac{2pi}{n}*k)} = cos(frac{2pi}{n}*k) + i sin(frac{2pi}{n}*k))，则(w_n^{-k})表示(w_n^k)的共轭复数。

从向量角度看，(w_n^k)和复平面中与实轴正向夹角为(frac{2pi}{n}*k)的单位向量一一对应。

根据上面那个表达式可推得：

  • (w_{mn}^{mk} = w_n^k)
  • (w_n^{k + frac{n}{2}} = w_n^{-k})

先将(A(x))按照(x)的阶的奇偶性分成两组，既：

[egin{aligned} A(x) &= (a_0 + a_2 x^2 + ··· + a_{n-2} x^{n-2}) + (a_1 x^1 + a_3 x^3 + ··· + a_{n-1} x^{n-1}) \ &=(a_0 + a_2 x^2 + ··· + a_{n-2} x^{n-2}) + x(a_1 + a_3 x^2 + ··· + a_{n-1} x^{n-2}) end{aligned} ]

令

[A_1(x) = a_0 + a_2 x + ··· + a_{n-2} x^{frac{n-2}{2}} \ A_2(x) = a_1 + a_3 x + ··· + a_{n-1} x^{frac{n-2}{2}} ]

则

[A(x) = A_1(x^2) + xA_2(x^2) ]

当(x = w_n^k)，(k in {0,1,2,···,frac{n}{2} - 1})，有

[egin{aligned} A(w_n^k) &= A_1((w_n^k)^2) + w_n^k*A_2((w_n^k)^2) \ &= A_1(w_n^{2k}) + w_n^k * A_2(w_n^{2k}) \ &= A_1(w_{frac{n}{2}}^k) + w_n^k * A_2(w_{frac{n}{2}}^k) end{aligned} ]

当(x = w_n^{k + frac{n}{2}})，(k in {0,1,2,···,frac{n}{2} - 1})，有

[egin{aligned} A(w_n^{k + frac{n}{2}}) &= A_1((w_n^{k + frac{n}{2}})^2) + w_n^{k + frac{n}{2}} * A_2((w_n^{k + frac{n}{2}})^2) \ &= A_1(w_n^{2k + n}) + w_n^{k + frac{n}{2}} * A_2(w_n^{2k + n}) \ &= A_1(w_n^{2k + n}) - w_n^k * A_2(w_n^{2k + n}) \ &= A_1(w_n^{2k}) - w_n^k * A_2(w_n^{2k}) \ &= A_1(w_{frac{n}{2}}^k) - w_n^k * A_2(w_{frac{n}{2}}^k) end{aligned} ]

如果已知(A_1(x))和(A_2(x))在(x = w_{frac{n}{2}}^k)，(k in {0,1,2,···,frac{n}{2} - 1})处的值，那么就可以在(O(n))的时间内求得(A(x))的点值表达式：(((w_n^0,A(w_n^0)),(w_n^1,A(w_n^1)),···,(w_n^{n-1},A(w_n^{n-1}))))。

求解(A_1(x))和(A_2(x))在(x = w_{frac{n}{2}}^k)，(k in {0,1,2,···,frac{n}{2} - 1})处的值与求解(A(x))在(x = w_n^k)，(k in {0,1,2,···, n-1})处的值的过程是一样的，只是规模减少了一半，运用递归分析法可概括得：

[egin{aligned} T(n) &= 2T(frac{n}{2}) + O(n) \ &=O(nlg(n)) end{aligned} ]

拿个多项式模拟一下上述表达式蕴含的递归过程，如图：

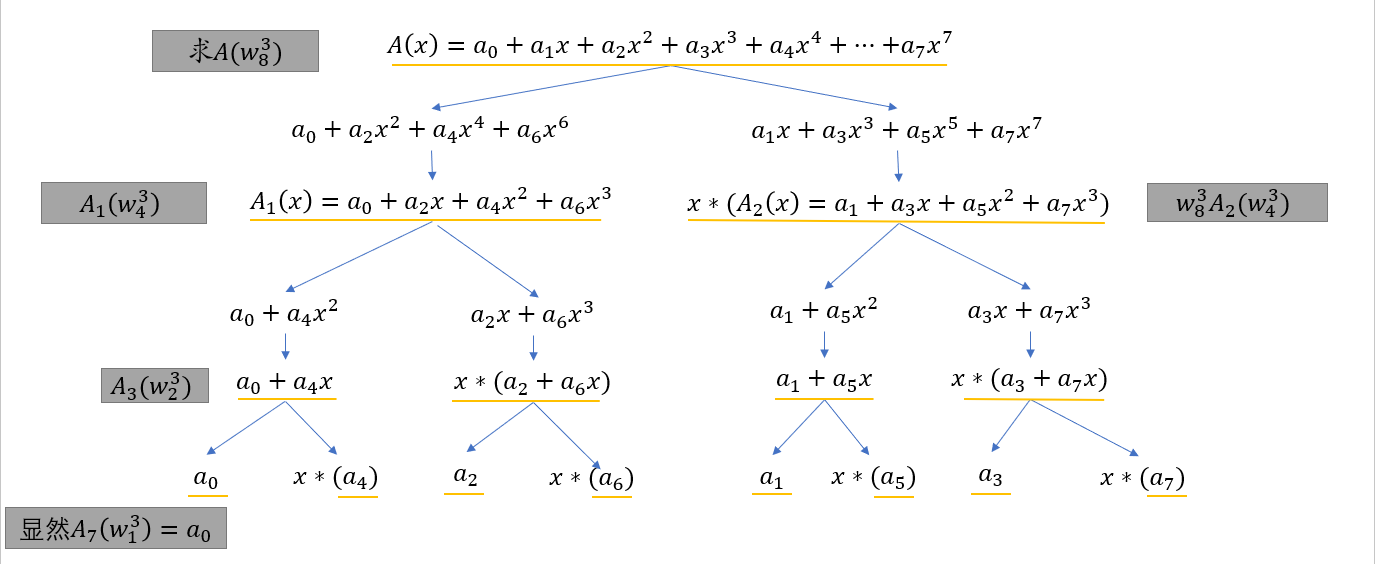
code

struct complex_number {
    double a, b;
    complex_number() { a = 0, b = 0; }
    complex_number(double a, double b): a(a), b(b) {}

    complex_number operator + (const complex_number& o) const {
        return complex_number(a + o.a, b + o.b);
    } 
    complex_number operator - (const complex_number& o) const {
        return complex_number(a - o.a, b - o.b);
    }
    complex_number operator * (const complex_number& o) const {
        return complex_number(a * o.a - b * o.b, a * o.b + b * o.a);
    }
    complex_number complex_conjugate() {
        return complex_number(a, -b);
    }
};

const int maxn = 100005;

complex_number cn[maxn];

complex_number w(int n, int k) {
    return complex_number(cos(2 * atan(1) * 4.0 * k / n), sin(2 * atan(1) * 4.0 * k / n));
}

void DFT(complex_number* A, int n) {
    if (n == 1) return;

    const int m = n >> 1;
    static complex_number buf[maxn];   

    for (int i = 0; i < m; i++) {
        buf[i] = A[i << 1];
        buf[i + m] = A[i << 1 | 1];
    }

    memcpy(A, buf, sizeof(complex_number) * n);

    complex_number *A1 = A, *A2 = A + m;

    DFT(A1, m);
    DFT(A2, m);

    for (int i = 0; i < m; i++) {
        complex_number temp = w(n, i);
        buf[i] = A1[i] + temp * A2[i];
        buf[i + m] = A1[i] - temp * A2[i];
    }

    memcpy(A, buf, sizeof(complex_number) * n);
}

点值表达式 ( ightarrow) 系数表达式 [ Inverse Discrete Fourier Transform ]

假设 (d_k = A(w_n^k) = sum_{i=0}^{n-1}a_i (w_n^k)^i)，(k in {0,1,2,···, n-1})，构造如下多项式：

[F(x) = d_0 + d_1 x^1 + d_2 x^2 + ··· + d_{n-1} x^{n-1} ]

假设 (c_k = F(w_n^{-k}) = sum_{i = 0}^{n-1}d_i(w_n^{-k})^i)，(k in {0,1,2,···,n-1})，展开(d_i)得：

[egin{aligned} c_k &= sum_{i=0}^{n-1}[sum_{j=0}^{n-1}a_j(w_n^i)^j] *(w_n^{-k})^i \ &= sum_{i=0}^{n-1}sum_{j=0}^{n-1}a_j(w_n^i)^j(w_n^{-k})^i \ &= sum_{j=0}^{n-1}sum_{i=0}^{n-1}a_j(w_n^i)^j(w_n^{-k})^i & 交换求和顺序 \ &= sum_{j=0}^{n-1}a_j[sum_{i=0}^{n-1}(w_n^i)^j(w_n^{-k})^i] \ &= sum_{j=0}^{n-1}a_j[sum_{i=0}^{n-1}(w_n^{i})^{j-k}] \ &= {sum_{j=0,j eq k}^{n-1}a_j[sum_{i=0}^{n-1}(w_n^{i})^{j-k}]} + {a_k[sum_{i=0}^{n-1}(w_n^{i})^{0}]} \ &= {sum_{j=0,j eq k}^{n-1}a_j[sum_{i=0}^{n-1}(w_n^{i})^{j-k}]} +n*a_k end{aligned} ]

当(j eq k)时，令(j - k = heta)，有：

[egin{aligned} {sum_{j=0,j eq k}^{n-1}a_j[sum_{i=0}^{n-1}(w_n^{i})^{ heta}]} &= sum_{j=0,j eq k}^{n-1}a_j(w_n^0 + w_n^{ heta} + w_n^{2 heta}+···+ w_n^{(n-1) heta}) \ &= sum_{j=0,j eq k}^{n-1}a_j(frac{w_n^0(1-(w_n^{ heta})^n)}{1-w_n^{ heta}}) & 等比公式 \ &= sum_{j=0,j eq k}^{n-1}a_j(frac{1-(w_n^n)^{ heta}}{1-w_n^{ heta}}) \ &= sum_{j=0,j eq k}^{n-1}a_j(frac{1-(1)^{ heta}}{1-w_n^{ heta}}) \ &= sum_{j=0,j eq k}^{n-1}a_j(frac{0}{1-w_n^{ heta}}) \ &= 0 end{aligned} ]

故

[egin{aligned} c_k &= n * a_k \ a_k &= frac{c_k}{n} end{aligned} ]

所以只要求得了(F(x))的点值表达式：(((w_n^0, c_1), (w_n^{-1}, c_2), ···, (w_n^{-(n-1)},c_{n-1})))，那么就可以在(O(n))的时间内求得(F(x))的系数表达式：((a_0, a_1, a_2, ···, a_{n-1}))。

参考

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/zgglj-com/p/14263945.html