逻辑回归(Logistic Regression)是广义线性回归的一种。逻辑回归是用来做分类任务的常用算法。分类任务的目标是找一个函数,把观测值匹配到相关的类和标签上。比如一个人有没有病,又因为噪声的干扰,条件的描述的不够完全,所以可能不确定正确,还希望得到一个概率,比如有病的概率是80%。也即P(Y|X),对于输入X,产生Y的概率,Y可取两类,1或者0。
推导
Sigmod函数

相当于线性模型的计算结果来逼近真实01标记的对数几率。
他的导数:
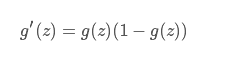
对数线性模型
概率P的值域是[0,1],线性函数的值域是((-infty ,+infty)),要将建立一个互相映射的函数关系,log函数在[0,1]上的值域是([-infty,0]),对P进行变换,使得变换之后的值域包含([0,+infty]),而(log(frac{p}{1-p}))满足要求。而这个称为logit变换。线性拟合
(log(frac{P(x; heta)}{1-P(x; heta)}) = heta x)
由此可得
(P(x; heta) = frac{1}{1+e^{-( heta x)}} = h_ heta (x) )
优点:可以算出落入 0 1的概率,无穷可导。
假设各个样本互相独立则,服从伯努利分布。
(P(y = 1 |x; heta) = h_ heta(x))
(P(y = 0 |x; heta) = 1 - h_ heta(x))
(P(y |x; heta) = h_ heta(x)^y(1 - h_ heta(x))^{1-y})
似然函数:
对于最大似然估计(MLE)就是已知了样本的分布,求最有可能导致这种分布的参数的值。也即是什么样的参数使得我们看到的这样一个数据分布出现的概率最大。
(L_ heta = prod_{i=1}^{m}h_{ heta}(x^{(i)})^{y^{(i)}} (1 - h_ heta(x^{(i)}))^{(1-y^{(i)})} )
(l( heta) = logL( heta) )

损失函数:
损失函数越小,模型越好。
损失函数是似然函数的取负之后得到,最小化的损失。
拆开写:
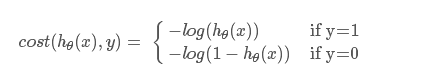
理解:当y =1时,如果h的预测结果也为1,则cost为0,如果h为0,则相当于预测相反,cost为无穷,类似的y=0的时候。
合并写,全体样本的损失函数为
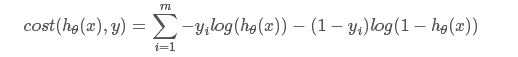
另外Softmax 只不过是2分类变成了K分类,本质上是一样的。
由于令损失函数等于0,无法求解析解。所以想到了用梯度下降,类似的算法还有BFGS,L-BFGS(Spark Mllib中用的),牛顿法,拟牛顿法,共轭梯度法。其中BFGS,和LBFGS由牛顿法而来,速度比梯度下降要快,但是复杂。
梯度下降:
(J( heta)) = cost

得到迭代子式:
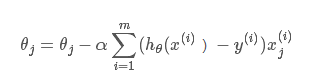
其中 (alpha)是步长。
SKLearn简单例子
if __name__ == "__main__":
path = u'iris.data' # 数据文件路径
#用pandas读数据
data = pd.read_csv(path)
x = data.values[:,:-1]
y = data.values[;-1]
le = LabelEncoder()
le.fit(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'])
y = le.transform(y)
x = StandardScaler().fit_transform(x)
logreg = LogisticRegression() # Logistic回归模型
logreg.fit(x, y.ravel()) # 根据数据[x,y],计算回归参数 ,y.ravel()是reshape成一列数,对原来的y的一个引用
# 训练集上的预测结果
y_hat = logreg.predict(x)
y = y.reshape(-1) # 此转置仅仅为了print时能够集中显示
print y_hat.shape # 不妨显示下y_hat的形状
print y.shape
result = (y_hat == y) # True则预测正确,False则预测错误
print y_hat
print y
print result
c = np.count_nonzero(result) # 统计预测正确的个数
print c
print 'Accuracy: %.2f%%' % (100 * float(c) / float(len(result)))
logL(θ)=∑i=1mlog[(hθ(xi)y(i)(1−hθ(x(i)))1−y(i))]=∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]