对于一个整数(a),若(b|a)则称(b)是(a)的因数。
正因数求法
1、试除法
对于一个数(n),其正因数必定不会超过(n),所以只用枚举一下(1-n)的所有数看看它是不是(n)的因数即可。复杂度(O(n))。
因为因数必定成对出现,所以只用枚举到(sqrt{n})即可。复杂度(O(sqrt{n}))。
这样求([1,n])中所有数的约数集合的时间复杂度为(O(nsqrt{n}))。
for (int i = 1; i <= n; i++) {
for (int j = 1; j * j <= i; j++) {
if (i % j) continue;
fac[i].push_back(j);
if (j * j != i) fac[i].push_back(i / j);
}
}
2、倍数法
用来快速求([1,n])中所有数的约数集合。
思想类似埃式筛法,用(i)去更新(i)的倍数。
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j += i) {
fac[j].push_back(i);
}
}
时间复杂度为调和级数:(O(nln{n})),同时说明([1,n])的约数个数大约为(nln{n})。
约数个数与约数和
将(n)质因数分解(n=Pi_{i=1}^{m} p_i^{c_i})可以得到(n)的约数集合(Pi_{i=1}^{m} p_i^{a_i}, a_i in [0,c_i])。
即可得到约数和为(sigma(n)=Pi_{i=1}^{m}sum_{j=0}^{c_i}p_i^{j})。
约数个数为(d(n)=Pi_{i=1}^{m} (c_i+1))
最大公约数
对于两个数(a,b),如果(d|a 且 d|b)则称其为公约数,其中最大的称为最大公约数记作(gcd(a,b))或((a,b))。
最大公约数的性质:
1、(gcd(a,b)=gcd(b,a))
2、(a|b)等价于(gcd(a,b)=a)。
3、(gcd(a,1)=1, gcd(a,0)=a)。
4、辗转相减法:(gcd(a,b)=gcd(a,b-a)=gcd(a,a-b))。
5、(gcd(ca, cb)=c imes gcd(a,b))。
6、(gcd(a+cb, b)=gcd(a,b))。
7、若(gcd(a,c)=1)则(gcd(a,bc)=gcd(a,b))
8、(gcd(a,b,c)=gcd(gcd(a,b),c))。
9、若(gcd(a,b)=1)则(gcd(ab,c)=gcd(a,c) imes gcd(b,c))。
10、若(d)是(a,b)的公约数,则(gcd(a/d,b/d)=gcd(a,b)/d)。
证明:
1、显然。
2、最大公约数不会超过两者中较小的一个(0是特例),得证。
3、一式由2即得证,二试所有数都是0的"约数"即得证。
4、设(d=gcd(a,b),a=dm,b=dn),有(gcd(m,n)=1),又有(gcd(m,m-n)=1)即得证。(gcd(m,m-n)=1)可由反证法得出。
5、显然。
6、由辗转相减法得证。
7、将a,b,c质因数分解即可得证。
8、设(d=gcd(a,b,c),a=dr,b=ds,c=dt,gcd(r,s,t)=1),(d|gcd(a,b)),可得(gcd(a,b))与(c)的最大公约数即为(d)。
9、同7的方法。
10、类似5
欧几里得算法:(gcd(a,b)=gcd(b,a\%b))。
证明:由辗转相减法得证。
int gcd(a,b) {return b == 0 ? a : gcd(b,a % b);}
最小公倍数
如果一个数(c)满足(a|c且b|c),则称(c)是(a,b)的公倍数,最小的(c)称为最小公倍数。
性质:
1、(lcm(a,b)=lcm(b,a))。
2、(lcm(a,1)=a, lcm(a,0)=0)。
3、(a|b)->(lcm(a,b)=b)。
4、(lcm(a,b,c)=lcm(lcm(a,b),c))。
5、(lcm(ac,bc)=c imes lcm(a,b))
6、(d|a且d|b),(lcm(d/a,d/b)=lcm(a,b)/d)。
7、(gcd(a,b) imes lcm(a,b)=a imes b)。
主要证明性质7(也是主要用来求lcm的方法)。
设(d=gcd(a,b)),则(a=dm,b=dn),则(lcm)得是(m,n,d)的倍数又((m,n)=1)所以(lcm(a,b)=dmn)。
最大公因数与最小公倍数的唯一分解:
(a=Pi_{i=1}^{m} p_i^{a_i},b=Pi_{i=1}^{m} p_i^{b_i})(没有的话指数就是0)。
则(gcd(a,b)=Pi_{i=1}^{m} p_i^{min(a_i,b_i)},lcm(a,b)=Pi_{i=1}^{m} p_i^{max(a_i,b_i)})。
习题:hankson的趣味题
欧拉函数
记([1,n])中与(n)互质的数的个数为(phi(n)),即为欧拉函数。
求欧拉函数的公式:(n imes Pi_{i=1}^{m} frac{p_i-1}{p_i})
用简单的容斥即可得证。
欧拉函数的性质:
(gcd(a,b)=1 -> phi(ab)=phi(a) imes phi(b))(积性函数的性质)
1~n中与(n)互质的数的和为(phi(n) imes frac{n}{2})
对于质数(p)如果(n\%p==0且n\%p^2!=0)则(phi(n)=phi(frac{n}{p}) imes (p-1))(由积性函数的性质得证)
对于质数(p)如果(n\%p==0且n\%p^2==0)则(phi(n)=phi(frac{n}{p}) imes p)(展开即可得证)
对于质数(p)有(sum_{i=0}^n phi(p^i)=p^n)
证明:
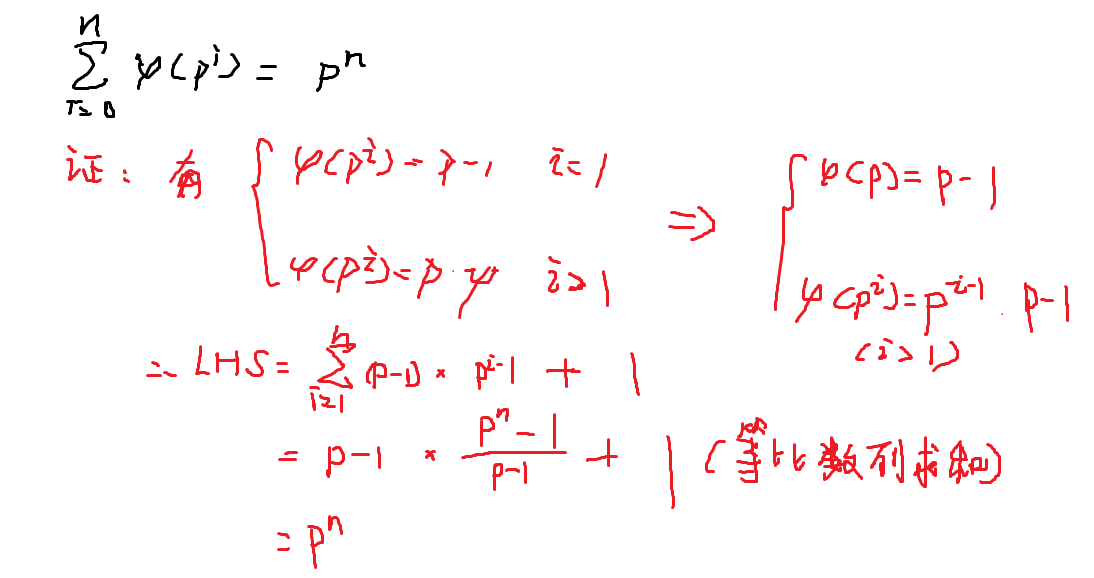
(sum_{d|n} phi(d) = n)
有关欧拉函数的应用:这篇博客写得不错