高斯消元
考虑如何解下面的方程组:
$a_{11}x_1+a_{12}x_2+...+a_{1n}x_n=y_1$
$a_{21}x_1+a_{22}x_2+...+a_{2n}x_n=y_2$
...
$a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n=y_n$
求满足条件的$x_1,x_2...x_m$。
把系数抽象成矩阵:
a11 a12 ... a1n
a21 a22 ... a2n
...
an1 an1 ... ann
再将其变为增广矩阵:
a11 a12 ... a1n b1
a21 a22 ... a2n b2
...
an1 an1 ... ann b2
高斯消元即在增广矩阵上通过初等行变换而消成对角矩阵。
初等行变换:
1、交换两行
2、将某行同时乘上某个数
3、将某行的几倍加到另一行上
其实就是在做加减消元的过程。
具体来讲,我们枚举每个要消的未知数$x_i$。然后留下$a_{ii}$,其余行第i列全通过初等行变换变为0。
这要求之前的数全为0。我们通常找到最大的$a_{ji}$和$a_{ii}$换来保持精度。
最后的答案即为$frac{B[i]}{A[i][i]}$。
一个例子(从网上借鉴的):
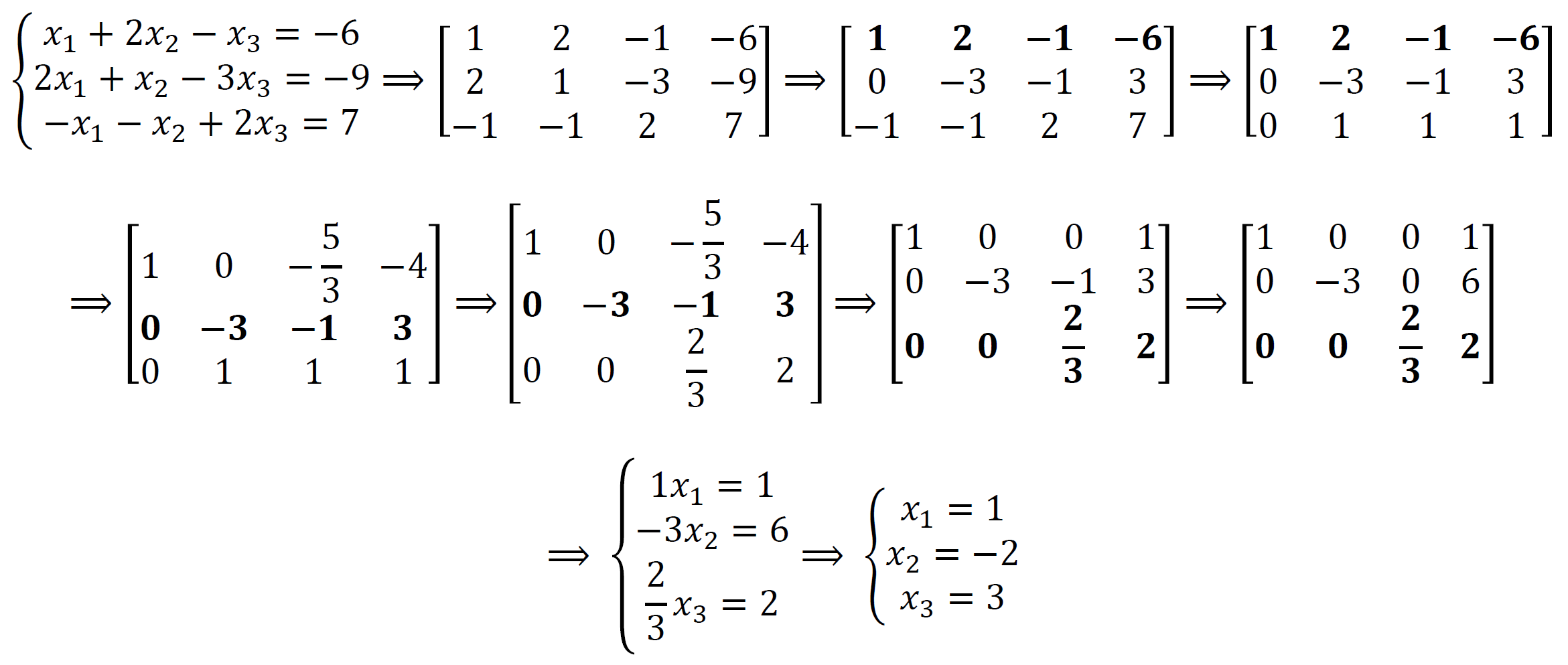
模板:
void Gauss() { for (int i = 1; i <= n; i++) { int mx = i; for (int j = i + 1; j <= n; j++) { if (A[j][i] > A[mx][i]) { mx = j; } } for (int j = i; j <= n; j++) { swap(A[i][j], A[mx][j]); } swap(B[i], B[mx]); if (!A[i][i]) continue; for (int j = 1; j <= n; j++) { if (i == j) continue; double Rate = A[j][i] / A[i][i]; for (int k = i; k <= n; k++) { A[j][k] -= A[i][k] * Rate; } B[j] -= B[i] * Rate; } } }
消元过程中可能出现某一行全为0但b不为0,这种情况误解。如果某一行全为0而b也为0则有无数解。注意先判误解再判无数解。
若系数不全为0的行有k个,则主元有k个,自由元有n-k个(存在解得情况下)。
不过还有可能出现这种情况,要特判。
这种情况可以这么写:
有对应的题目:[SDOI2006]线性方程组
#include <bits/stdc++.h> using namespace std; const double eps = 1e-8; const int N = 110; int n; double a[N][N], b[N]; int sgn(double x) { if (fabs(x) < eps) return 0; if (x > 0) return 1; return -1; } void deburg() { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) printf("%.2lf ", a[i][j]); printf("%.2lf ", b[i]); } printf(" "); } int Gauss() { int now = 1; for (int i = 1; i <= n; i++) { int mx = now; for (int j = now + 1; j <= n; j++) { if (fabs(a[j][i]) > fabs(a[mx][i])) { mx = j; } } for (int k = 1; k <= n; k++) swap(a[now][k], a[mx][k]); swap(b[now], b[mx]); if (fabs(a[now][i]) < eps) { continue; } double div = a[now][i]; for (int j = i; j <= n; j++) a[now][j] /= div; b[now] /= div; for (int j = 1; j <= n; j++) { if (now == j) continue; double base = a[j][i] / a[now][i]; for (int k = i; k <= n; k++) a[j][k] -= a[now][k] * base; b[j] -= b[now] * base; } now++; } if (now <= n) { while (now <= n) { if (b[now++] != 0) return -1; } return 0; } return 1; } int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { scanf("%lf", &a[i][j]); } scanf("%lf", &b[i]); } int ans = Gauss(); if (ans <= 0) { printf("%d", ans); } else { for (int i = 1; i <= n; i++) { printf("x%d=%.2lf ", i, b[i]); } } return 0; }
这篇题解讲得蛮清楚的。
习题:
线性空间
定义:关于向量加法与数乘封闭的集合
如果向量$b$,能被向量$a_1, a_2, dots, a_n$通过数乘表示出来即存在实数$x_1, x_2,dots, x_n$使得$b=a_1x_1, a_2x_2, dots, a_nx_n$。
所有$b$构成一个线性空间,$a_1, a_2, dots, a_n$称为生成子集。
给定若干向量$a_1, a_2, dots, a_n$若存在$a_i$能被其它表示出来则称其线性相关,若不行则称其线性无关。
线性无关的向量组称为构成的线性空间的基底(简称基)。
这个基底的向量的数量称为维数。
对于一个$n*m$的矩阵其$n$个行向量构成的线性空间的维数称为其行秩,同样我们可以定义列秩。
对于一个矩阵其行秩与列秩相等,统称为矩阵的秩。
对这个矩阵高斯消元求出主元的个数即为矩阵的秩。
有先选费用小的高斯消元即可。
#include <iostream> #include <cstdio> #include <algorithm> #include <cmath> using namespace std; const long double eps = 1e-5; struct node{ long double b[510]; int c; }a[510]; int n, m; int ans; void Gauss() { int now = 1; for (int i = 1; i <= m; i++) { int cha = -1; for (int j = now; j <= n; j++) { if (fabs(a[j].b[i]) > eps && (cha == -1 || a[cha].c > a[j].c)) { cha = j; } } if (cha == -1) continue; for (int j = 1; j <= m; j++) swap(a[now].b[j], a[cha].b[j]); swap(a[now].c, a[cha].c); for (int j = 1; j <= n; j++) { if (j == now) continue; double base = a[j].b[i] / a[now].b[i]; for (int k = i; k <= m; k++) { a[j].b[k] -= a[now].b[k] * base; } } ans += a[now].c; now++; if (now > n) break; } printf("%d %d", now - 1, ans); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { scanf("%Lf", &a[i].b[j]); } } for (int i = 1; i <= n; i++) scanf("%d", &a[i].c); Gauss(); return 0; }