回到队里2周,开始系统复习旧算法和学习新算法,整理之前没整理过的算法
什么是强连通分量
强连通图(Strongly Connect Graph)是指:如果在有向图 (G) 中,对于每两个不同的点 (v_i,v_j),有一条 (v_i) 到 (v_j) 的简单路径存在,那么称 (G) 是强连通图。
有向图的极大强连通子图称为有向图的强连通分量(Strongly Connected Component,简称SCC)。
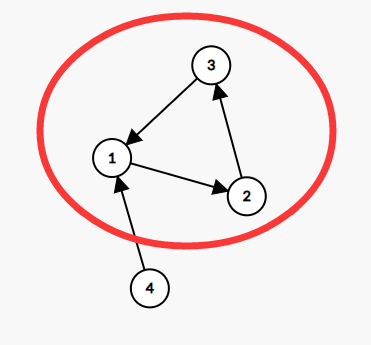
如图,图中点1、2、3构成了一个强连通分量。
Tarjan算法求解SCC
基本原理
Tarjan算法(以发现者Robert Tarjan命名)是一个在图中查找强连通分量的算法。
此算法以一个有向图作为输入,并按照所在的强连通分量给出其顶点集的一个划分。图中的每个节点只在一个强连通分量中出现,即使是在有些节点单独构成一个强连通分量的情况下(比如图中出现了树形结构或孤立节点)。
算法的基本思想如下:任选一节点开始进行深度优先搜索(若深度优先搜索结束后仍有未访问的节点,则再从中任选一点再次进行)。搜索过程中已访问的节点不再访问。搜索树的若干子树构成了图的强连通分量。
节点按照被访问的顺序存入堆栈中。从搜索树的子树返回至一个节点时,检查该节点是否是某一强连通分量的根节点并将其从堆栈中删除。如果某节点是强连通分量的根,则在它之前出堆栈且还不属于其他强连通分量的节点构成了该节点所在的强连通分量。
来源:Wikipedia
以上是Tarjan算法比较高端的定义,现在我们来简易的理解一下它的原理。
Tarjan算法的核心是维护两个重要的数组:dfn[]和low[]
dfn[] 表示的是“时间戳”,dfn[i] 代表了节点 (i) 被遍历到的次序,注意 dfn[] 的值不可以改变。
low[] 则表示的是当前子树中,仍在堆栈里的最小时间戳。容易知道,只要两个节点拥有相等的 low 值,那么它们一定在同一个子树里,同时也就在同一个 SCC 中。
在每次搜索的时候,要初始化dfn[x]=low[x]=++total(这里 total 初始值为 0),因为每一个节点都可以看作一个 SCC ,所以这里暂时把 low[x] 赋值为时间戳 dfn[x]。
我们从当前节点出发,搜索这个节点延伸出的子树。在搜索子树的过程中,假设遇到一个点没有搜索过,那么递归搜索它,搜索之后,用搜索节点的 low 值更新当前节点的 low 值;如果这个点已经被搜索过了,那么用搜到点的 dfn 值更新当前点的 low 值。
当无法继续搜索时,如果 dfn[x]==low[x] 那么在堆栈中所有满足上述条件的点构成一个 SCC 。
模拟Tarjan工作方式
给一张有向图,如下。
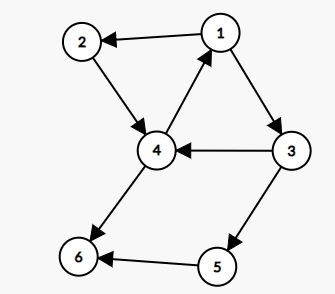
模拟Tarjan工作方式
给一张有向图,如下。
从节点 1 开始 DFS ,把遍历到的点加入栈中。搜索到节点 (x=6) 时,无法继续向下搜索。
dfn:1,0,2,0,3,4
low:1,0,2,0,3,4
stack:1,3,5,6
此时 dfn[6]==low[6],退栈直到栈顶元素为 (x) 为止。此时,找到 6 为一个 SCC。
同样,回到 (x=5) 时,无法继续搜索,退栈。发现 5 也是一个强连通分量。
更新:
dfn:1,0,2,0,3,4
low:1,0,2,0,3,4
stack:1,3
发现 3 还有子节点 4 ,4 有子节点 1 和 6(6 已经被搜过,不再搜索),那么 3 和 4 的 low 值被 1 的 dfn 值更新。
更新:
dfn:1,0,2,5,3,4
low:1,0,1,1,3,4
stack:1,3,4
3、4 不能继续搜索,回到 1 ,1 还有子节点 2 ,然后到子节点 4,此时 4 在栈中,更新 2 的 low 值为 4 的 dfn 值 5。
更新:
dfn:1,6,2,5,3,4
low:1,5,1,1,3,4
stack:1,3,4,2
回到 1 ,无法继续搜索,不停退栈,那么 1,3,4,2 四个点构成一个 SCC。
综上,这个有向图的强连通分量有:5、6、(1,2,3,4)。
Part 3 例题应用(代码实现)
使用 Tarjan 算法的目的是实现:重构图。
对于一个有向有环图,使用 Tarjan 进行 SCC 构建(缩点)之后,它就变成了一个DAG。
对于 DAG ,有很多方便的性质,比如拓扑DP,你甚至可以在上面跑网络流。
我们结合一道例题来看:洛谷P3387【模板】缩点
在这个问题中,需要我们求出最大点权和,但是显然不可以直接 DP ,因为一旦一个点被更新之后,我们用它更新其他点之后,这个点还有可能被再次更新(因为有环的存在)。也就是不满足我们所说的 DP 需要满足的“无后效性原则”。
那么怎么办呢?题目中给出:边可以重复走,但是遇到的点只计算一次点权。想到可以对这个图进行 Tarjan 缩点:只要我们走到其中任意一个 SCC 里,我们就可以获得这个 SCC 包含的所有点的点权,并且从这个 SCC 包含的点中任意一条边离开这个 SCC。何况,在 Tarjan 之后,这个有向有环图变成了一个 DAG,我们可以进行拓扑排序,然后 DP 来解决上面所说的后效性问题。(用拓扑序 DP 可以保证更新一个点之后,这个点在之后的求解中不再更新,因为该点入度为 0 ,无论如何也不可能再走到这个点)。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<stack>
#include<vector>
#include<queue>
//using namespace std;
typedef long long ll;
const int maxm=100005;
const int maxn=10005;
struct Point{
int value;
std::vector<int>to;
};
struct Point SCC[maxn];
std::vector<int>v[maxm];
std::stack<int>stk;
int visit[maxn],dfn[maxn],low[maxn],Value_of_each_Point[maxn],Belong_to_SCC[maxn],DP[maxn];
//依次表示:i号点是否访问过,dfn,low,i号点的点权,i号点属于哪个SCC,DP数组
int n,m,cnt,tot;
//cnt表示SCC个数,tot同上的total
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
void Tarjan(int x){
dfn[x]=low[x]=++tot;
stk.push(x);
visit[x]=1;
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(!dfn[y]){
Tarjan(y);
low[x]=std::min(low[x],low[y]);
}else if(visit[y]){
low[x]=std::min(low[x],dfn[y]);
}
}//更新
if(low[x]==dfn[x]){//不能搜索了,如果满足条件,开始退栈并统计
int Last_Element;
cnt++;//SCC个数++
do{
Last_Element=stk.top();
visit[Last_Element]=0;
Belong_to_SCC[Last_Element]=cnt;//表示这个点属于标号为cnt的SCC
SCC[cnt].value+=Value_of_each_Point[Last_Element];
//cnt号SCC权值+=该点点权
stk.pop();
}while(stk.size() && x!=Last_Element);
}
return;
}
int Toposort(){
int In[maxn];
std::queue<int>Queue;
memset(In,0,sizeof In);
memset(DP,0,sizeof DP);
for(int i=1;i<=cnt;i++)
for(int j=0;j<SCC[i].to.size();j++)
In[SCC[i].to[j]]++;//统计入度
for(int i=1;i<=cnt;i++)
if(In[i]==0){
Queue.push(i);//找到入度为0的点,开始拓扑排序
DP[i]=SCC[i].value;
}
while(Queue.size()){
int From=Queue.front();
Queue.pop();
for(int j=0;j<SCC[From].to.size();j++){
int To=SCC[From].to[j];
DP[To]=std::max(DP[To],DP[From]+SCC[To].value);
//用当前SCC更新它可以到的其他SCC
In[To]--;//这些SCC的入度--
if(In[To]==0)
Queue.push(To);//如果没有入度了,进入队列准备拓扑排序
}
}
int ans=0;
for(int i=1;i<=cnt;i++)
ans=std::max(DP[i],ans);//统计输出答案
return ans;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++)
Value_of_each_Point[i]=read();
for(int i=0,x,y;i<m;i++){
x=read(),y=read();
if(x!=y)
v[x].push_back(y);
}//读入原图边
for(int i=1;i<=n;i++)
if(!dfn[i])
Tarjan(i);//防止图不连通,对每一个点Tarjan
for(int i=1;i<=n;i++)
for(int j=0;j<v[i].size();j++)
if(Belong_to_SCC[i]!=Belong_to_SCC[v[i][j]])
SCC[Belong_to_SCC[i]].to.push_back(Belong_to_SCC[v[i][j]]);
//重构图,扫描每个点属于哪个SCC,可以到达的点属于哪个SCC,在这两个SCC之间建边,注意判断自环,否则拓扑排序会炸
printf("%d",Toposort());
return 0;
}
PS:感谢sy巨神帮我调代码