数论——素数

转自：http://www.cnblogs.com/linyujun/p/5198832.html

整合：https://blog.csdn.net/x_i_y_u_e/article/details/46365549

整合：https://blog.csdn.net/qq_43332305/article/details/82959066

说明

1. π(x) ，素数分布函数，为小于等于 x 的素数的个数。
2. 当 x 趋于 无穷大时，π(x) 与 x / lnx等价。
3. 当 x 趋于 无穷大时，1~x 中所有素数的倒数和与 $ln ln x$ 等价。
4. factor(x) 表示x的因子个数，比如 factor(6) = 4。

素数

定义

除了1和它本身以外不再有其他的因数的数。也叫质数。

素数判定

根据素数的定义判定（复杂度$O(sqrt{n})$）

代码如下

//素数
inline bool isPrime(const LL x) {
    if (x <= 1)return false;
    for (LL i = 2; i * i <= x; i++)if (x % i == 0)return false;
    return true;
}

埃拉托斯特尼筛法

原理：如果找到一个质数，那么这个质数的倍数都不是质数。

这个方法能在 $O(n ln ln n)$ 的时间复杂度内筛选出 1~n 中的所有素数。示例图如下：

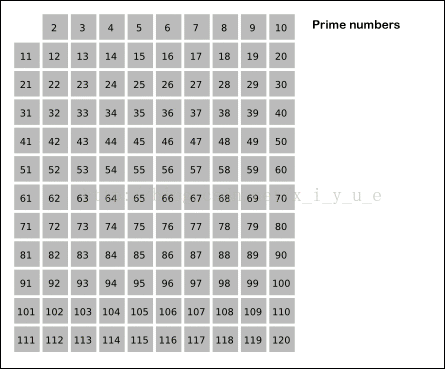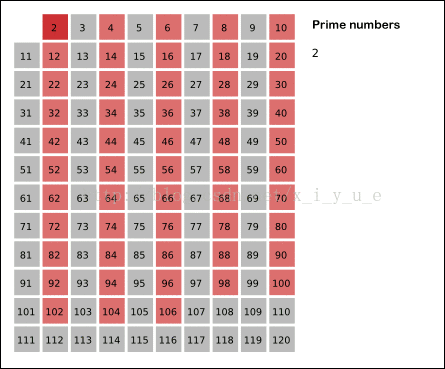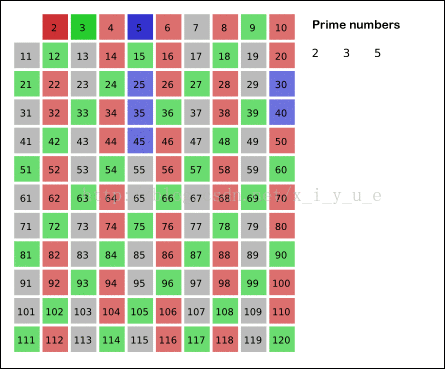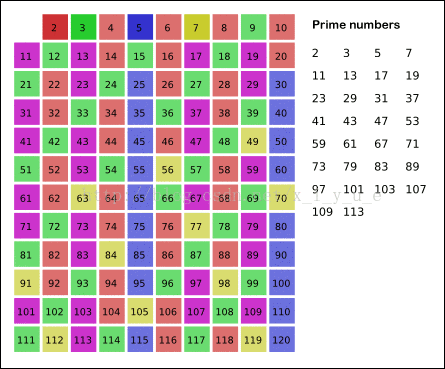
复杂度说明如下

设 p_i 为 1~n 中第 i 个素数。

对于每一个 p_i，都要筛去 n / p_i 个数，因此，筛选行为总数为 n * (1/p₁ + 1/p₂ +……+ 1/p_π(n)) ，等价于 $nln ln n$。

代码如下

bool primes[maxN];
inline void Eratosthenes(){
    For(i, 2, maxN) primes[i] = true;//先全部初始化为质数 
    For(i, 2, maxN) {
        if(primes[i]){//如果i是质数 
            for(int j = 2 * i; j < maxN; j += i){//从i的两倍开始的所有倍数 
                primes[j] = false; 
            }
        }
    }
}

这个代码还能进一步优化，一个合数如果有因数，那么必定是成对存在，也就是筛子只用判断其中一个因数就可以了，比如15=3*5，在3的时候已经把15给筛掉了，何必去循环到5呢？循环到根号 n 即可。

第二层循环中，j 可以从 i * i开始，因为 i * (i - 1)， i * (i - 2) 等等这些数必然已经被比 i 小的质数筛掉了。

代码如下（优化后）

bool primes[maxN];
inline void Eratosthenes(){
    For(i, 2, maxN) primes[i] = true;//先全部初始化为质数 
    for(int i = 2; i * i < maxN; ++i) {
        if(primes[i]){//如果i是质数 
            //从i * i开始的所有倍数
            for(int j = i * i; j < maxN; j += i){
                primes[j] = false; 
            }
        }
    }
}

线性筛法（欧拉筛法）

以空间换时间的方法，一个数只会经过一次，能把时间复杂度降为 O(n)。

代码如下

const int N = 1000;
bool isPrime[N + 7];//isPrime[i]表示i是不是质数 
VI primes;//primes用来存质数 
inline void Euler(){
    For(i, 2, N) isPrime[i] = true;//初始化为质数 
    For(i, 2, N) {
        if(isPrime[i]) primes.PB(i);//把质数存起来 
        for(int j = 0; j < primes.size() && i * primes[j] <= N; ++j) {
            isPrime[i * primes[j]] = false;
            if(i % primes[j] == 0) break;//保证每个合数被它最小的质因数筛去 
        }
    }    
}

算术基本定理

定义

任何一个大于1的自然数 N，如果N不为质数，那么N可以唯一分解成有限个质数的乘积。当然 N 为质数的时候就是本身，没必要分解。

设 N 的质因子为：p₁， p₂， ……，p_π(N)。（从小到大排）

设对应质因子个数为：e₁， e₂， ……，e_π(N)。

则定义的公式表示为：$$N = prod_{i=1}^{π(N)} {p_i}^{e_i}$$

约数个数定理

$$factor(N) = prod_{i=1}^{π(N)} {e_i + 1}$$

反素数

定义

对${forall_{0 < i < n}}$ ，都有 factor(n) > factor(i)，称 n 为反素数。

性质

1. 一个反素数的质因子必然是从2开始连续的质数。
2. 分解质因数后对应质因子的个数满足：e₁ >= e₂ >=……>= e_π(n)。

 求不大于 n 的最大反素数代码

LL n;
// ans = （最大反素数，相应因子数） 
PLL ans;
int primes[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53};

// x 表示当前处理到第 x 个质数
// ret为当前选择下的质数乘积 
// pcnt 为 1~x-1 个质数中，每个质数选择数量+1的乘积 
// limit 表示第x个质数选则的上限 
// cnt表示第 x 个质数已经选了多少个 
inline void dfs(int x = 0, LL ret = 1, LL pcnt = 1, int limit = inf, int cnt = 0) {
    if(ret > n || limit < cnt) return;
    LL tmp = pcnt * (cnt + 1);
    if(ans.sd < tmp || ans.sd == tmp && ans.ft > ret) ans = MP(ret, tmp);
    
    if(n / ret >= primes[x])dfs(x, ret * primes[x], pcnt, limit, cnt + 1); // 选 primes[x]
    if(cnt) dfs(x + 1, ret, tmp, cnt, 0); // 不选 primes[x]
}