SVM回归
我们之前提到过,SVM算法功能非常强大:不仅支持线性与非线性的分类,也支持线性与非线性回归。它的主要思想是逆转目标:在分类问题中,是要在两个类别中拟合最大可能的街道(间隔),同时限制间隔侵犯(margin violations);而在SVM回归中,它会尝试尽可能地拟合更多的数据实例到街道(间隔)上,同时限制间隔侵犯(margin violation,也就是指远离街道的实例)。街道的宽度由超参数ϵ控制。下图展示的是两个线性SVM回归模型在一些随机线性数据上训练之后的结果,其中一个有较大的间隔(ϵ = 1.5),另一个的间隔较小(ϵ = 0.5)。
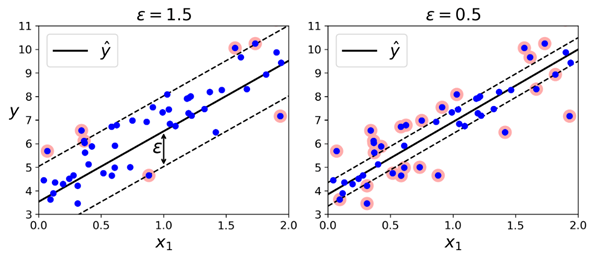
如果后续增加的训练数据包含在间隔内,则不会对模型的预测产生影响,所以这个模型也被称为是ϵ-insensitive。
我们可以使用sk-learn的LinearSVR类训练一个SVM回归,下面的代码对应的是上图中左边的模型(训练数据需要先做缩放以及中心化的操作,中心化又叫零均值化,是指变量减去它的均值。其实就是一个平移的过程,平移后所有数据的中心是(0, 0)):
from sklearn.svm import LinearSVR svm_reg = LinearSVR(epsilon=1.5) svm_reg.fit(X, y)
再处理非线性的回归任务时,也可以使用核化的SVM模型。例如,下图展示的是SVM回归在一个随机的二次训练集上的表现,使用的是二阶多项式核:
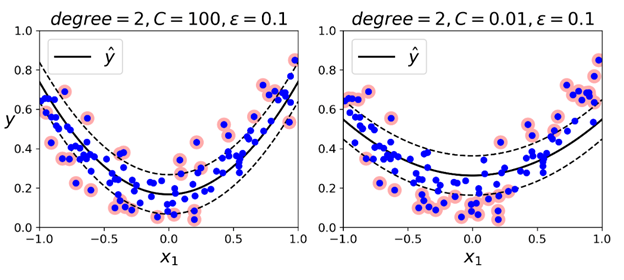
左边的图中有一个较小的正则(超参数C的值较大),而右边图中的正则较大(较小的C值)。
下面的代码上图中左边的图对应的模型,使用的是sk-learn SVR类(支持核方法)。SVR类等同于分类问题中的SVC类,并且LinearSVR类等同于分类问题中的LinearSVC类。LinearSVR类会随着训练集的大小线性扩展(与LinearSVC类一样);而SVR类在训练集剧增时,速度会严重下降(与SVC类一致):
from sklearn.svm import SVR svm_poly_reg = SVR(kernel='poly', degree=2, C=100, epsilon=0.1) svm_poly_reg.fit(X, y)
SVMs也可以用于异常点(值)检测,具体可以参考sk-learn文档。
原理解释
在这章我们会解释SVM如何做预测,以及训练算法是如何工作的,先从线性SVM分类器开始。
首先,我们将所有的模型参数放入一个向量θ,包括偏置项参数θ0以及输入特征的权重θ1 到 θn,并且给所有数据实例增加一个偏置项x0 = 1。这里偏置项称为b,特征权重向量称为w。
决策方法与预测
线性SVM分类器模型在做预测时,对于输入的实例x,它会计算决策函数wTx + b = w1x1 + ⋯ + wnxn + b:如果结果是正的,则预测的类别ŷ就属于正类(1),否则属于反类(0),如下公式所示:
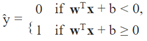
下面我们看一下SVM在之前iris数据集上训练后的决策函数图:
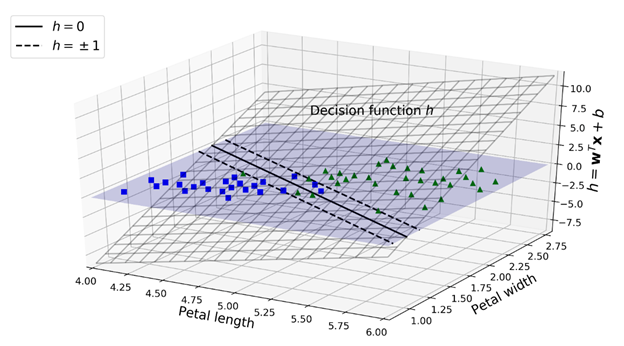
这是一个二维平面,因为数据集有两个特征(petal width与petal length)。决策边界是由那些让决策函数等于0的点组成:也就是两个平面的交线(由上图中实线表示)。
虚线代表的是令决策函数等于1或-1的点:这两条虚线平行且距决策边界的距离相等,组成了一个间隔。训练线性SVM分类器就是找到一对w与b的值,让这个间隔尽可能的宽的同时,还要避免或是限制间隔侵犯(margin violation)。避免间隔侵犯的结果就是硬间隔(hard margin),限制间隔侵犯的结果就是软间隔(soft margin)。
训练目标
上图的例子中我们看到这个决策函数的图像是一个平面,并且有一个坡度。这个坡度等同的是权重向量w的范数(norm):∥ w ∥。如果我们将这个坡度除以2,则那些令决策函数等于±1 的点会离决策边界两倍远。换句话说,坡度除以2会让间隔增加2倍。如下图所示:
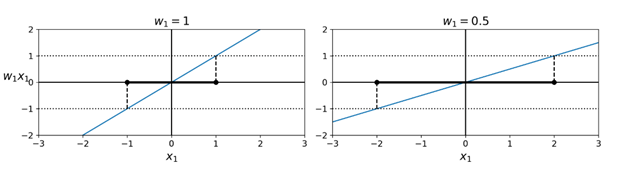
所以我们希望最小化 ∥ w ∥ 的值以获取一个更大的间隔。不过,如果我们同时也希望避免间隔入侵(硬间隔),则我们需要让决策函数对所有训练数据中的“正”训练实例计算结果大于1,而对所有“负”训练实例的计算结果小于-1。如果我们对负实例(也就是y(i) = 0)定义t(i) = –1,对正实例(y(i) = 1)定义t(i) = 1,则我们可以使用约束t(i)(wT x(i) + b) ≥ 1 定义所有实例。
所以我们接下来可以将硬间隔SVM分类器目标表示为一个带约束的优化问题,如下公式:
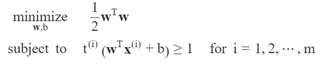
这里可以看到,我们优化的不是∥ w ∥,而是½wTw,它等同于½∥ w ∥2。因为½∥ w ∥2的导数非常简单(也就是w),而∥ w ∥ 在w=0时不可微。优化算法在可微函数上工作效果更好。
为了达到软间隔(soft margin)目标,我们需要为每个实例i引入一个松弛变量ζ(i) ≥ 0,这个变量衡量的是第ith个实例被允许入侵间隔的程度。我们现在有两个冲突的目标:让松弛变量尽可能的小,以减少间隔入侵;同时还要让 ½∥ w ∥2 尽可能的小,以增加间隔。所以这就是为什么算法中引入超参数C:这个参数可以让我们定义这两个目标之间的权衡(tradeoff)。对应的带约束优化问题为:
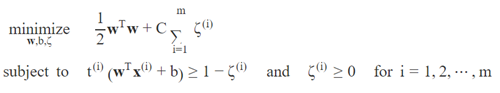
二次规划
硬间隔与软间隔问题都是带线性约束的凸二次优化问题,这种就是常说的二次规划(Quadratic Programming,QP)问题。有很多现成的解决办法用于解决QP问题,在这不会深入讨论。这种常规问题的公式如下所示:

需要注意的是表达式Ap ≤ b 定义了nc的约束:p⊺ a(i) ≤ b(i) for i = 1, 2, ⋯, nc, 这里a(i)代表的是包含了A的第ith行的向量,b(i)代表的是b的ith第个元素。
如果我们按下面的参数设置QP参数,则可以得到硬间隔线性SVM分类器的目标:

一个训练硬间隔线性SVM分类器的方法是使用已有的OP问题解决方法,传入上述参数即可。求得的结果向量p会包含偏执项b=p0,以及特征权重wi = pi for i = 1, 2, ⋯, n。类似的,也可以使用QP问题解决方案解决软间隔问题。
不过在使用核方法时,我们会使用另一个不同的带约束的优化问题。
在线SVM(online SVM)
在这章结束之前,我们快速地看一下在线SVM分类器(在线学习是指递增的训练,一般在一个新实例到达时就训练一次)。
对于线性SVM分类器,一种方法是使用梯度下降(例如使用SGDClassifier)最小化以下损失函数:
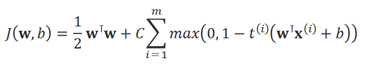
这个损失函数是由原始问题推导得出,但是它的收敛速度相比基于QP方法的收敛会慢特别多。在这个损失函数中,第一个累加会推进模型去找一个较小的权重向量w,继而产生一个更大的间隔。第二个累加会计算所有的间隔入侵(margin violations)。一个实例如果是远离街道、且在它所属正确的那一侧,则它的间隔入侵为0;否则它的间隔入侵则为距离正确那一侧街道的距离的比例。最小化这个项,会确保模型尽可能少地造成间隔入侵。
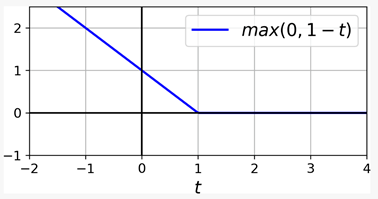
最后提一下HINGE LOSS,我们之前在训练SVM时使用的是这个损失函数。它的函数为max(0, 1-t)。在 t ≥ 1时,输出为0。它的导数在t < 1 时等于 -1,在t > 1 时等于0 ;在t=1时不可微,不过仍可以在使用梯度下降时,使用t=1 时的任何次导数(也就是说,任何在-1到0之间的值)。函数图如下:
在在线SVM中,也是可以实现在线核化SVM的,例如使用“Incremental and Decremental SVM Learning” 或”Fast Kernel Classifiers with Online and Active Learning”。不过这些是通过Matlab和C++实现的。对于大型的非线性问题,我们其实可以考虑使用神经网络。