比赛网址:https://codeforces.com/contest/1391
A. Suborrays
网址:https://codeforces.com/contest/1391/problem/A
A permutation of length (n) is an array consisting of (n) distinct integers from (1) to n in arbitrary order. For example, ([2,3,1,5,4]) is a permutation, but ([1,2,2]) is not a permutation ((2) appears twice in the array) and ([1,3,4]) is also not a permutation ((n=3) but there is (4) in the array).
For a positive integer (n), we call a permutation (p) of length (n) good if the following condition holds for every pair (i) and (j) ((1≤i≤j≤n)) —
- ((p_i OR p_{i+1} OR … OR p_{j−1} OR p_j))(≥){(j−i+1)}, where OR denotes the bitwise OR operation.
In other words, a permutation (p) is good if for every subarray of (p), the OR of all elements in it is not less than the number of elements in that subarray.
Given a positive integer (n), output any good permutation of length (n). We can show that for the given constraints such a permutation always exists.
Input
Each test contains multiple test cases. The first line contains the number of test cases (t) ((1≤t≤100)). Description of the test cases follows.
The first and only line of every test case contains a single integer (n) ((1≤n≤100)).
Output
For every test, output any good permutation of length (n) on a separate line.
Example
input
3
1
3
7
output
1
3 1 2
4 3 5 2 7 1 6
Note
For (n=3, [3,1,2]) is a good permutation. Some of the subarrays are listed below.
- (3 OR 1=3≥2 (i=1,j=2))
- (3 OR 1 OR 2=3≥3 (i=1,j=3))
- (1 OR 2=3≥2 (i=2,j=3))
- (1≥1 (i=2,j=2))
Similarly, you can verify that ([4,3,5,2,7,1,6]) is also good.
考虑到一个结论:(a|b≥a),所以随便排。
C ++ AC代码
#include<iostream>
#include<cstdio>
using namespace std;
int n;
int main()
{
int t;
scanf("%d", &t);
while(t --)
{
scanf("%d", &n);
for(int i = 1; i <= n; ++ i) printf("%d ", i);
puts("");
}
return 0;
}
B. Fix You
网址:https://codeforces.com/contest/1391/problem/B
Consider a conveyor belt represented using a grid consisting of (n) rows and (m) columns. The cell in the (i)-th row from the top and the (j)-th column from the left is labelled ((i,j)).
Every cell, except ((n,m)), has a direction R (Right) or D (Down) assigned to it. If the cell ((i,j)) is assigned direction R, any luggage kept on that will move to the cell ((i,j+1)). Similarly, if the cell ((i,j)) is assigned direction D, any luggage kept on that will move to the cell ((i+1,j)). If at any moment, the luggage moves out of the grid, it is considered to be lost.
There is a counter at the cell ((n,m)) from where all luggage is picked. A conveyor belt is called functional if and only if any luggage reaches the counter regardless of which cell it is placed in initially. More formally, for every cell ((i,j)), any luggage placed in this cell should eventually end up in the cell ((n,m)).
This may not hold initially; you are, however, allowed to change the directions of some cells to make the conveyor belt functional. Please determine the minimum amount of cells you have to change.
Please note that it is always possible to make any conveyor belt functional by changing the directions of some set of cells.
Input
Each test contains multiple test cases. The first line contains the number of test cases (t) ((1≤t≤10)). Description of the test cases follows.
The first line of each test case contains two integers (n,m) ((1≤n≤100, 1≤m≤100)) — the number of rows and columns, respectively.
The following n lines each contain m characters. The (j)-th character in the (i)-th line, (a_{i,j}) is the initial direction of the cell ((i,j)). Please note that (a_{n,m}= C).
Output
For each case, output in a new line the minimum number of cells that you have to change to make the conveyor belt functional.
Example
input
4
3 3
RRD
DDR
RRC
1 4
DDDC
6 9
RDDDDDRRR
RRDDRRDDD
RRDRDRRDR
DDDDRDDRR
DRRDRDDDR
DDRDRRDDC
1 1
C
output
1
3
9
0
Note
In the first case, just changing the direction of ((2,3)) to D is enough.
You can verify that the resulting belt is functional. For example, if we place any luggage at ((2,2)), it first moves to ((3,2)) and then to ((3,3)).
In the second case, we have no option but to change the first (3) cells from D to R making the grid equal to RRRC.
这就是图的连通性。
C ++ AC代码
#include<iostream>
#include<cstdio>
using namespace std;
const int SIZE = 100 + 5;
char map[SIZE][SIZE];
int n, m;
int main()
{
int t;
scanf("%d", &t);
while(t --)
{
scanf("%d %d", &n, &m);
for(int i = 0; i < n; ++ i) scanf("%s", map[i]);
int cnt = 0;
for(int i = 0; i < m; ++ i)
{
if(map[n - 1][i] == 'D') ++ cnt;
}
for(int i = 0; i < n; ++ i)
if(map[i][m - 1] == 'R') ++ cnt;
printf("%d
", cnt);
}
return 0;
}
C. Cyclic Permutations
网址:https://codeforces.com/contest/1391/problem/C
A permutation of length (n) is an array consisting of (n) distinct integers from (1) to (n) in arbitrary order. For example, [2,3,1,5,4] is a permutation, but ([1,2,2]) is not a permutation ((2) appears twice in the array) and ([1,3,4]) is also not a permutation ((n=3) but there is (4) in the array).
Consider a permutation (p) of length (n), we build a graph of size (n) using it as follows:
- For every (1≤i≤n), find the largest (j) such that (1≤j<i) and (p_j>p_i), and add an undirected edge between node (i) and node (j)
- For every (1≤i≤n), find the smallest (j) such that (i<j≤n) and (p_j>p_i), and add an undirected edge between node (i) and node (j)
In cases where no such (j) exists, we make no edges. Also, note that we make edges between the corresponding indices, not the values at those indices.
For clarity, consider as an example (n=4), and (p=[3,1,4,2]); here, the edges of the graph are ((1,3),(2,1),(2,3),(4,3)).
A permutation (p) is cyclic if the graph built using p has at least one simple cycle.
Given (n), find the number of cyclic permutations of length (n). Since the number may be very large, output it modulo 109+7.
Please refer to the Notes section for the formal definition of a simple cycle
Input
The first and only line contains a single integer (n) ((3≤n≤10^6)).
Output
Output a single integer (0≤x<10^9+7), the number of cyclic permutations of length (n) modulo (10^9+7).
Examples
input
4
output
16
input
583291
output
135712853
Note
There are (16) cyclic permutations for (n=4). ([4,2,1,3]) is one such permutation, having a cycle of length four: (4→3→2→1→4).
Nodes (v_1, v_2, …, v_k) form a simple cycle if the following conditions hold:
- (k≥3).
- (v_i≠v_j) for any pair of indices (i) and (j). ((1≤i<j≤k))
- (v_i) and (v_{i+1}) share an edge for all (i) ((1≤i<k)), and (v_1) and (v_k) share an edge.
这道题很考察算法基本功。
首先,我最开始考虑怎么样能形成环?事实上,该序列是有环的充分必要条件是存在(a_i>a_j<a_k)((i<j<k)),否则不存在。
正着想,想了半晌考虑给该序列“塞”上一个数,用计数方法发现重复状态没法统计;
那么,什么情况不存在呢??事实上,只要该序列先单调递增再单调递减,满足单峰状态即可,而单增和单减则是特殊情况。
会发现满足一个递推式:设(f[i])代码(i)的排列中有多少不满足题意,必有:(f[i]=f[i-1]<<1)。关于该式可以考虑将最大的数放在峰上,都有两种选择。
C ++ AC代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int mod = 1000000007;
int n;
int main()
{
scanf("%d", &n);
long long tmp = 1, p = 1;
for(int i = 2; i <= n; ++ i)
{
tmp = (long long) tmp * i % mod;
p = (long long) p * 2ll % mod;
}
printf("%d
", (tmp - p + mod) % mod);
return 0;
}
D. 505
网址:https://codeforces.com/contest/1391/problem/D
A binary matrix is called good if every even length square sub-matrix has an odd number of ones.
Given a binary matrix a consisting of (n) rows and (m) columns, determine the minimum number of cells you need to change to make it good, or report that there is no way to make it good at all.
All the terms above have their usual meanings — refer to the Notes section for their formal definitions.
Input
The first line of input contains two integers (n) and (m) ((1≤n≤m≤10^6) and (n⋅m≤10^6)) — the number of rows and columns in (a), respectively.
The following (n) lines each contain (m) characters, each of which is one of (0) and (1). If the (j)-th character on the (i)-th line is (1), then (a_{i,j}=1). Similarly, if the (j)-th character on the (i)-th line is (0), then (a_{i,j}=0).
Output
Output the minimum number of cells you need to change to make (a) good, or output (−1) if it's not possible at all.
Examples
input
3 3
101
001
110
output
2
input
7 15
000100001010010
100111010110001
101101111100100
010000111111010
111010010100001
000011001111101
111111011010011
output
-1
Note
In the first case, changing (a_{1,1}) to (0) and (a_{2,2}) to (1) is enough.
You can verify that there is no way to make the matrix in the second case good.
Some definitions —
- A binary matrix is one in which every element is either (1) or (0).
- A sub-matrix is described by (4) parameters — (r_1), (r_2), (c_1), and (c_2); here, (1≤r_1≤r_2≤n) and (1≤c_1≤c_2≤m).
- This sub-matrix contains all elements (a_{i,j}) that satisfy both (r_1≤i≤r_2) and (c_1≤j≤c_2).
- A sub-matrix is, further, called an even length square if (r_2−r_1=c_2−c_1) and (r_2−r_1+1) is divisible by (2).
又是一道状压。
很显然,当(min(n,m)>=4)时,此题无解。
至于剩余的数据该怎么处理。
首先,(n)和(m)中有一个数很小,因此,我们可以利用这个性质解题。
通常,状压DP伴随着预处理工作。
不妨设(n)最小,可以给(n)分类讨论:(n=2)时一种,(n=3)时一种;
把(0-1)变为二进制,对于当前的(mask),预处理满足题意的状态;
于是就有了转移方程:(dp[i,mask]=dp[i-1,premask]+calc(mask,digit[i])),其中(calc)代表当前状态与开始矩阵的不同位。
C ++ AC代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int SIZE = 1000000 + 5, INF = 1 << 30;
bool valid[10][10] = {};
int n, m, ans = INF, a[5][SIZE], digit[5], dp[SIZE][10];
int calc(int x)
{
int res = 0;
while(x)
{
if(x & 1) ++ res;
x >>= 1;
}
return res;
}
bool judge(int x, int y)
{
if(n == 3)
{
int x1 = x % 4, y1 = y % 4;
int x2 = x >> 1, y2 = y >> 1, cnt1, cnt2;
cnt1 = calc(x1) + calc(y1), cnt2 = calc(x2) + calc(y2);
if((cnt1 & 1) && (cnt2 & 1)) return true;
return false;
} else
{
if((calc(x) + calc(y)) & 1) return true;
return false;
}
}
void pre_work()
{
for(int i = 0; i < 1 << n; ++ i)
{
for(int j = i; j < 1 << n; ++ j)
{
valid[i][j] = valid[j][i] = judge(i, j);
}
}
memset(dp, 0x3f, sizeof(dp));
for(int i = 1; i <= m; ++ i)
{
digit[i] = 0;
for(int j = 1; j <= n; ++ j)
{
digit[i] = digit[i] << 1 | a[j][i];
}
}
return;
}
int main()
{
scanf("%d %d", &n, &m);
if(min(n, m) >= 4)
{
puts("-1");
return 0;
}
if(min(n, m) < 2)
{
puts("0");
return 0;
}
if(n > m)
{
swap(n, m);
for(int j = 1; j <= m; ++ j)
{
for(int i = 1; i <= n; ++ i)
{
scanf("%1d", &a[i][j]);
}
}
}
else
{
for(int i = 1; i <= n; ++ i)
{
for(int j = 1; j <= m; ++ j)
{
scanf("%1d", &a[i][j]);
}
}
}
pre_work();
for(int i = 0; i < 1 << n; ++ i) dp[1][i] = calc(i ^ digit[1]);
for(int i = 2; i <= m; ++ i)
{
for(int j = 0; j < 1 << n; ++ j)
{
for(int k = 0; k < 1 << n; ++ k)
{
if(valid[j][k]) dp[i][j] = min(dp[i][j], dp[i - 1][k] + calc(j ^ digit[i]));
}
}
}
for(int i = 0; i < 1 << n; ++ i) ans = min(ans, dp[m][i]);
printf("%d
", ans);
return 0;
}
E. Pairs of Pairs
网址:https://codeforces.com/contest/1391/problem/E
You have a simple and connected undirected graph consisting of (n) nodes and (m) edges.
Consider any way to pair some subset of these (n) nodes such that no node is present in more than one pair.
This pairing is valid if for every pair of pairs, the induced subgraph containing all (4) nodes, two from each pair, has at most (2) edges (out of the (6) possible edges). More formally, for any two pairs, ((a,b)) and ((c,d)), the induced subgraph with nodes {(a,b,c,d)} should have at most (2) edges.
Please note that the subgraph induced by a set of nodes contains nodes only from this set and edges which have both of its end points in this set.
Now, do one of the following:
Find a simple path consisting of at least (⌈n/2⌉) nodes. Here, a path is called simple if it does not visit any node multiple times.
Find a valid pairing in which at least (⌈n/2⌉) nodes are paired.
It can be shown that it is possible to find at least one of the two in every graph satisfying constraints from the statement.
Input
Each test contains multiple test cases. The first line contains the number of test cases (t) ((1≤t≤10^5)). Description of the test cases follows.
The first line of each test case contains (2) integers (n,m) ((2≤n≤5⋅10^5, 1≤m≤10^6)), denoting the number of nodes and edges, respectively.
The next (m) lines each contain (2) integers (u) and (v) ((1≤u,v≤n, u≠v)), denoting that there is an undirected edge between nodes (u) and (v) in the given graph.
It is guaranteed that the given graph is connected, and simple — it does not contain multiple edges between the same pair of nodes, nor does it have any self-loops.
It is guaranteed that the sum of (n) over all test cases does not exceed (5⋅10^5).
It is guaranteed that the sum of (m) over all test cases does not exceed (10^6).
Output
For each test case, the output format is as follows.
If you have found a pairing, in the first line output "PAIRING" (without quotes).
Then, output (k) ((⌈n/2⌉≤2⋅k≤n)), the number of pairs in your pairing.
Then, in each of the next (k) lines, output (2) integers (a) and (b) — denoting that (a) and (b) are paired with each other. Note that the graph does not have to have an edge between (a) and (b)!
This pairing has to be valid, and every node has to be a part of at most (1) pair.
Otherwise, in the first line output "PATH" (without quotes).
Then, output (k) ((⌈n/2⌉≤k≤n)), the number of nodes in your path.
Then, in the second line, output (k) integers, (v_1,v_2,…,v_k), in the order in which they appear on the path. Formally, (v_i) and (v_{i+1}) should have an edge between them for every (i) ((1≤i<k)).
This path has to be simple, meaning no node should appear more than once.
Example
input
4
6 5
1 4
2 5
3 6
1 5
3 5
6 5
1 4
2 5
3 6
1 5
3 5
12 14
1 2
2 3
3 4
4 1
1 5
1 12
2 6
2 7
3 8
3 9
4 10
4 11
2 4
1 3
12 14
1 2
2 3
3 4
4 1
1 5
1 12
2 6
2 7
3 8
3 9
4 10
4 11
2 4
1 3
output
PATH
4
1 5 3 6
PAIRING
2
1 6
2 4
PAIRING
3
1 8
2 5
4 10
PAIRING
4
1 7
2 9
3 11
4 5
Note
The path outputted in the first case is the following.
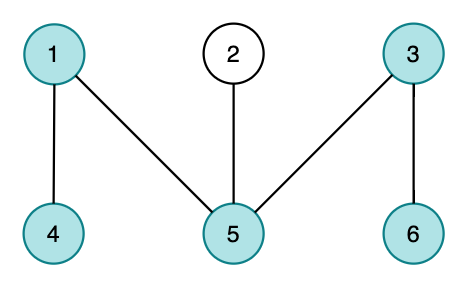
The pairing outputted in the second case is the following.
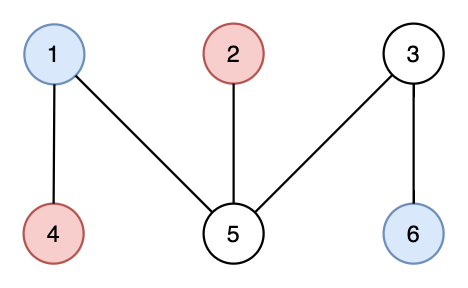
Here is an invalid pairing for the same graph — the subgraph {(1,3,4,5)} has (3) edges.
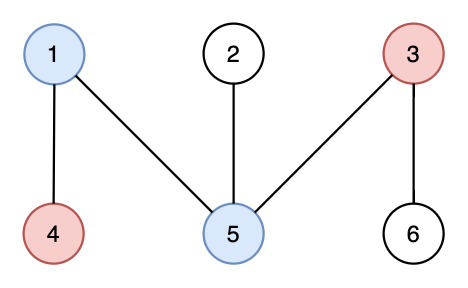
Here is the pairing outputted in the third case.
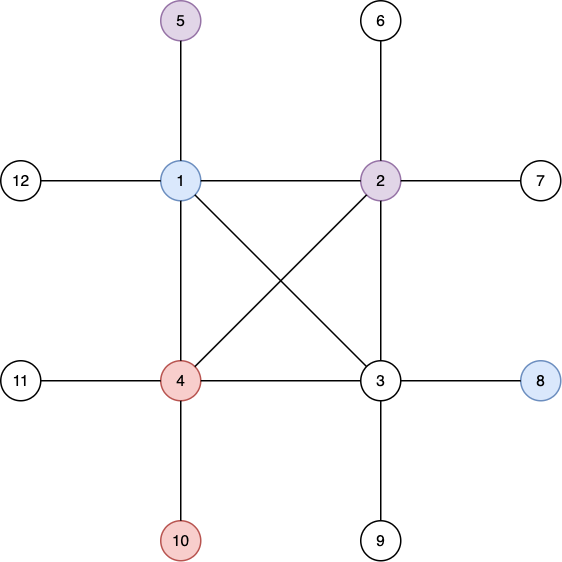
It's valid because —
- The subgraph {(1,8,2,5)} has edges ((1,2)) and ((1,5)).
- The subgraph {(1,8,4,10)} has edges ((1,4)) and ((4,10)).
- The subgraph {(4,10,2,5)} has edges ((2,4)) and ((4,10)).
Here is the pairing outputted in the fourth case.
任选一个点,dfs一遍;
若发现有节点深度大于(n/2),直接输出。
否则就考虑配对。
找 每一层相邻两个节点进行配对最终的配对即为答案。
证明:
首先,最深结点深度保证了配对数量至少可以满足题意;
考虑每一层中任意两个节点(a,b),如果连边,则必不在同一层;
如果任选两对不同深度的配对,不妨设((a,b)(c,d))。则(c)与该配对无法有两条边。
C ++ TLE代码(有大佬帮忙改改吗???)
#include<iostream>
#include<cstring>
#include<vector>
#include<cstdio>
#include<cmath>
using namespace std;
const int SIZE = 500000 + 5;
vector <int> G[SIZE], table[SIZE];
bool vis[SIZE];
int n, m, pair_num = 0, dep[SIZE], fa[SIZE], ans[SIZE][2];
bool dfs(int u)
{
pair_num -= table[dep[u]].size() >> 1;
table[dep[u]].push_back(u);
pair_num += table[dep[u]].size() >> 1;
if(dep[u] >= (n + 1) >> 1)
{
puts("PATH");
printf("%d
", dep[u]);
printf("%d ", u);
while(u != 1)
{
u = fa[u];
printf("%d ", u);
}
return true;
}
for(int i = 0; i < G[u].size(); ++ i)
{
int v = G[u][i];
if(vis[v]) continue;
vis[v] = true;
fa[v] = u;
dep[v] = dep[u] + 1;
if(dfs(v)) return true;
}
return false;
}
int main()
{
int t;
scanf("%d", &t);
while(t --)
{
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++ i) G[i].clear(), table[i].clear();
int u, v;
for(int i = 0; i < m; ++ i)
{
scanf("%d %d", &u, &v);
G[u].push_back(v), G[v].push_back(u);
}
memset(vis, false, sizeof(vis));
vis[1] = true;
dep[1] = 1;
pair_num = 0;
if(dfs(1)) puts("");
else
{
puts("PAIRING");
printf("%d
", pair_num);
for(int i = 1; i <= n / 2; ++ i)
{
for(int j = 0; j < table[i].size() >> 1; ++ j)
{
printf("%d %d
", table[i][j << 1], table[i][j << 1 | 1]);
}
}
}
}
return 0;
}
总结
感觉C、D、E出的很有区分度,让我学到不少东西。