神经网络

神经网络

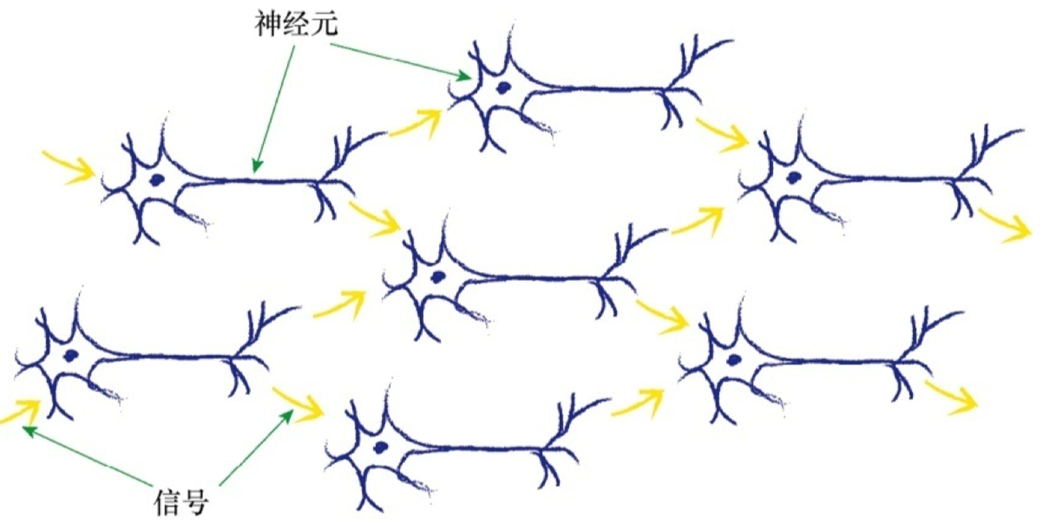
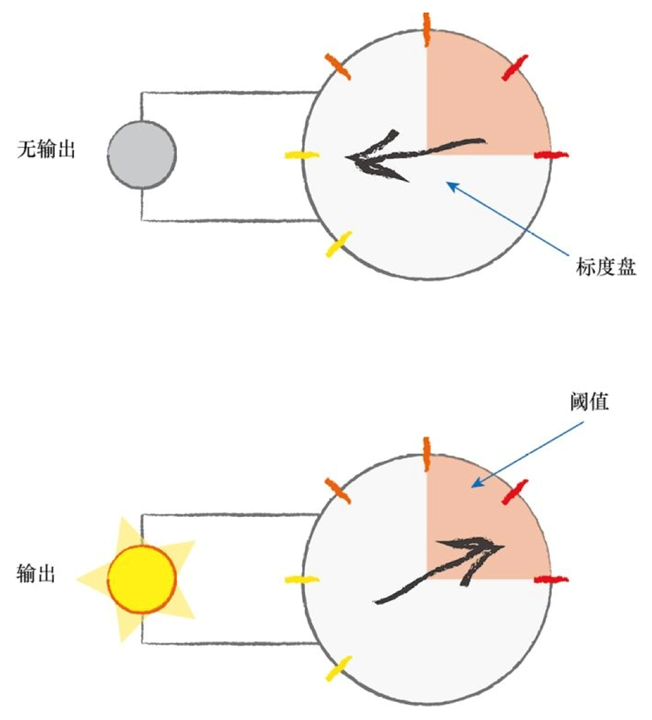
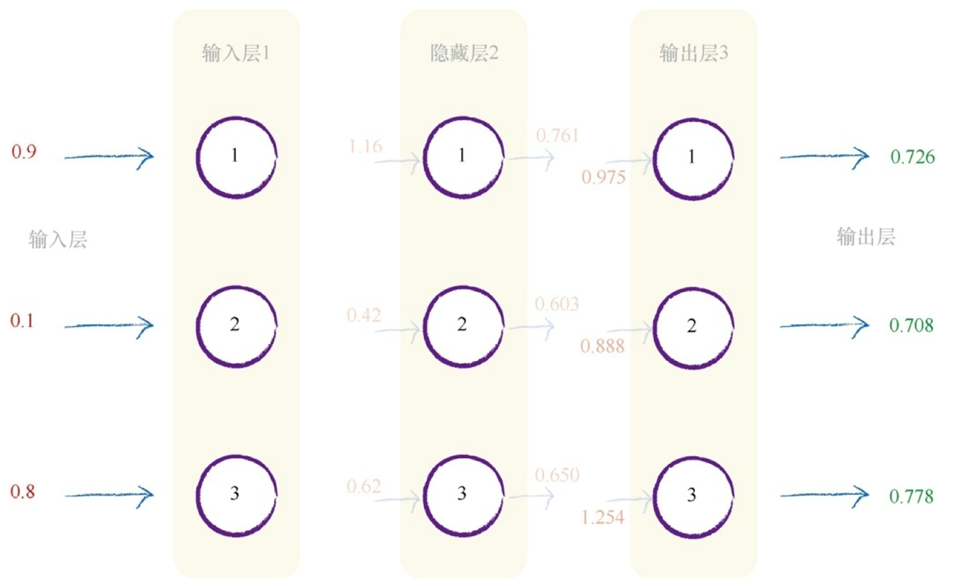
　　神经网络的一个重要的设计特征来源于线性分类器的局限性（不能用一条直线把根本性的问题划分开来），神经网络的核心思想是使用多个分类器一起工作。这时，你可以想象，多条直线可以分离出异常形状的区域，对各个区域进行分类。如下图所示，输入信号通过神经元的每一层，当输入值超过了threshold，足够接通电路，才会产生可以到达下一层的电信号，此时被激活。

            

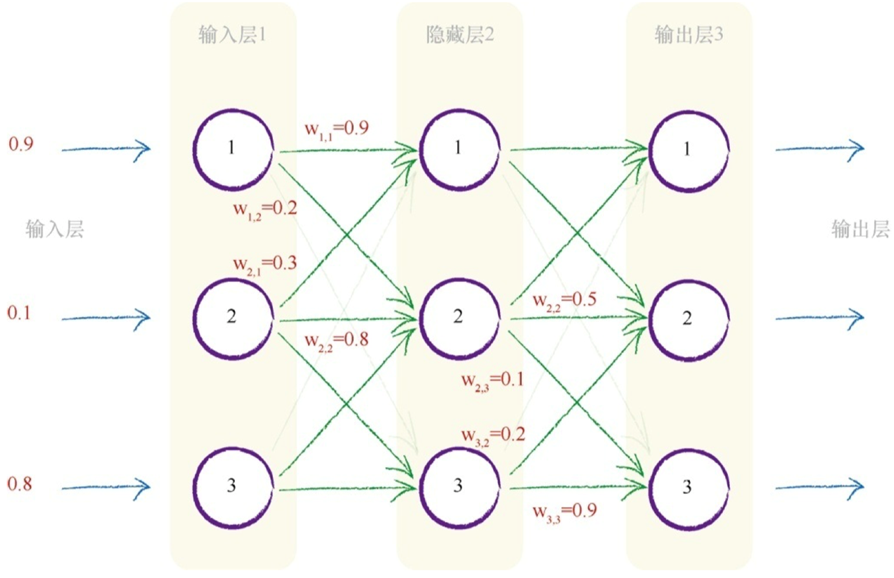
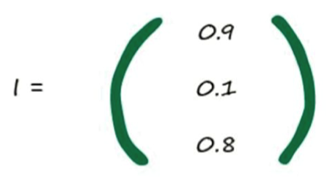
　　每一 层的计算可以转换为矩阵运算， X = W * I

            

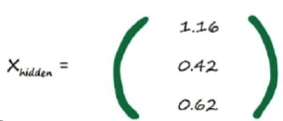
　　计算出X_hidden后，我们要通过激活函数使其变化平滑（在超过阈值后，输入值可能会有一次阶跃，可能出现间断点）

    

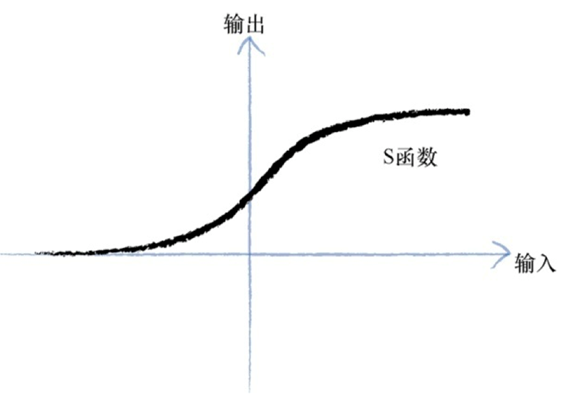
 　　采用sigmoid()函数后，输入变量的范围从（-∞，+∞）映射到（0,1），这样便于我们用概率去描述一个分类器，比定义阈值方便一些。sigmoid()函数本身是一个单调上升的函数，它是连续不间断的，可以缓解模型中点的阶跃突变导致的不连续即为上述problem。

 

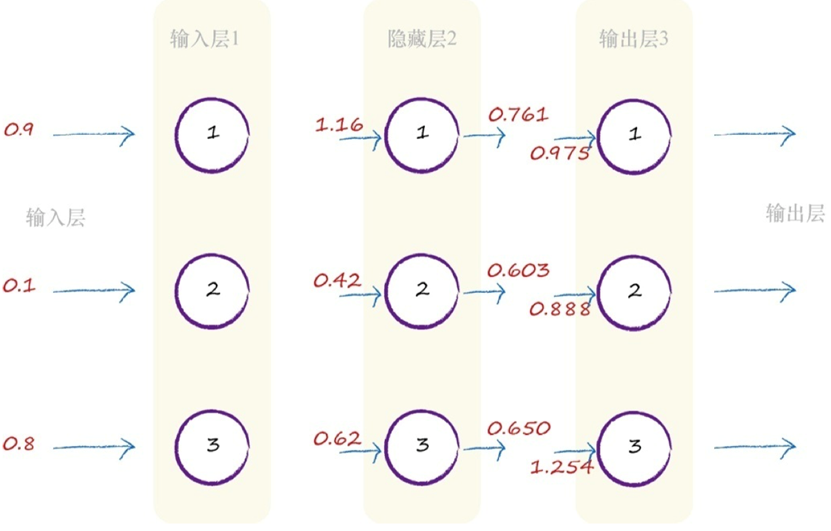
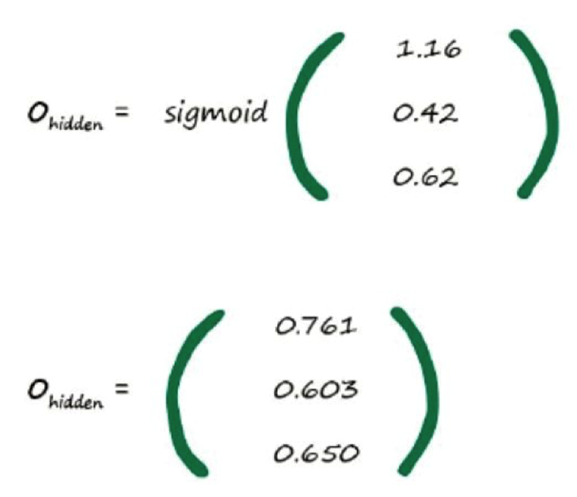
　　经过这样的计算，得出最后的output，然后我们可以通过真实数据得知此次的output与真实值之间的差距，计算出error，当我们知道error后，怎么把error告诉前面的层----"你们的前面那些层，weight设置不合理，这里错了呢"

  

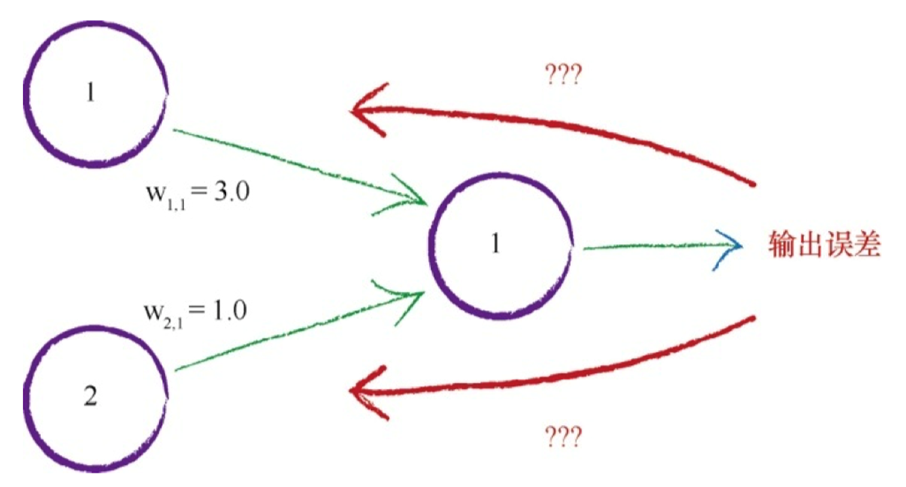
 　　在神经网络中，有两件事使用了权重。（1）将信号从输入向前传播到输出层；（2）将误差从输出向后传播到网络中，这种称为反向传播。

                              

                    

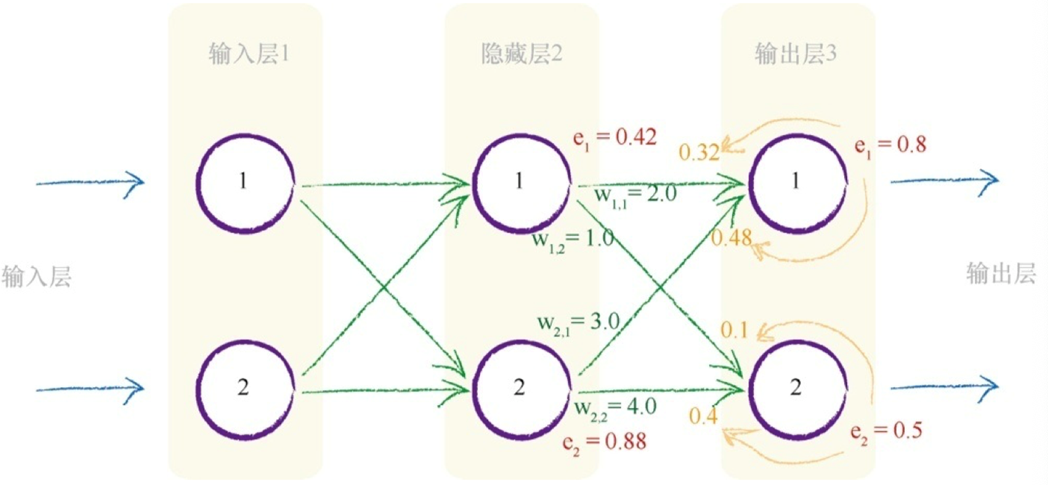
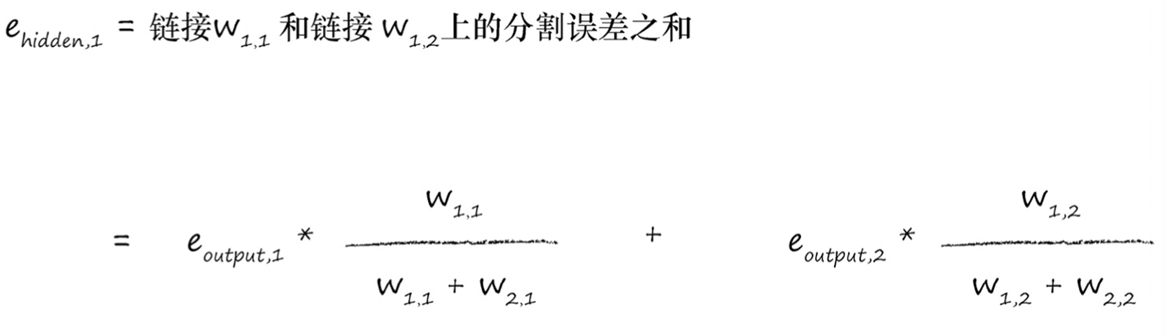
　　神经网络是通过链接权重进行学习的，上述方法就是按照链路权重的比例来分隔输出层的误差，然后在每个内部节点处重组这些误差。

              

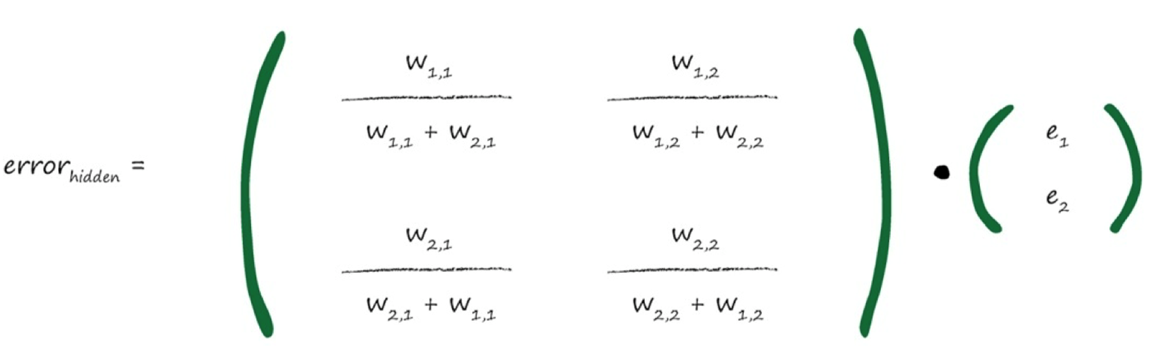
　　忽略分母（归一化因子），各weight矩阵对角线进行翻转，装置为$ W^T $

                    

                  

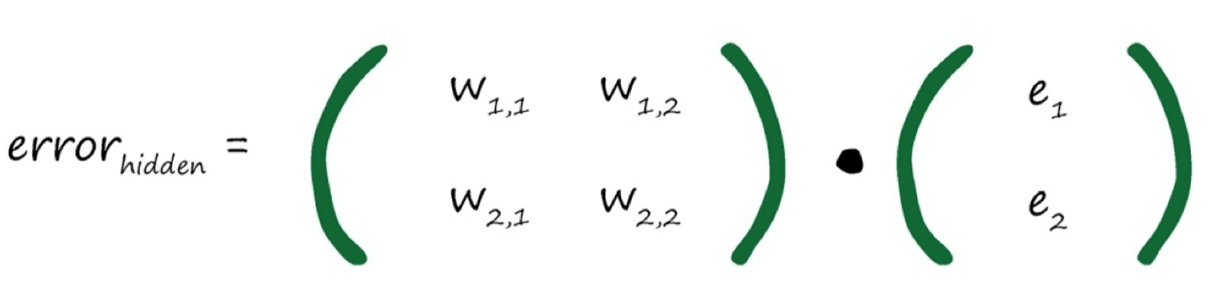
     以误差来指导使用误差来指导如何调整链接权重，从而改进神经网络输出类似线性分类器所做的事情神经网络节点都不是简单的线性分类器，能使用一些微妙的代数来直接计算出权重的正确值吗？

                      

     

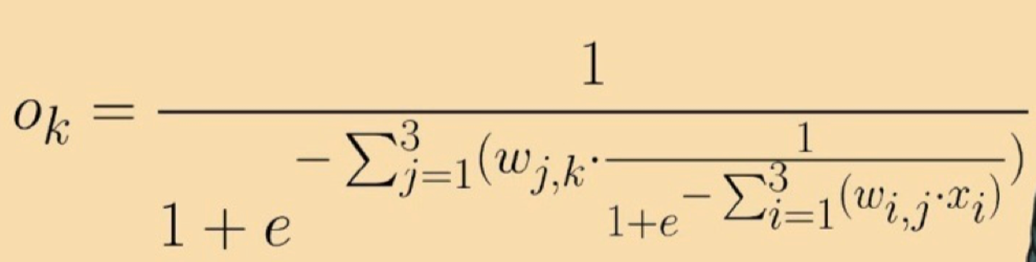
    （1）能够表示所有的权重如何生成神经网络输出的数学表达式过于复杂， 难以求解；（2）太多的权重组合，难以逐个测试，以找到一种最好的组合；（3）训练数据可能不足，不能正确地教会网络；（4）训练数据可能有错误，因此即使假设完全正确，神经网络可以学到一些东西，但却有缺陷（4）神经网络本身可能没有足够多的层或节点，不能正确地对问题的解进行建模；（5）如果从实际出发可以找到一种办法，虽然这种方法从数学角度而言并不完美，但是由于这种方法没有做出虚假的 ；（6）理想化假设，因此实际上带来了更好的结果。

    这时我们需要引入梯度的概念，对于梯度下降这里不多赘述，之后会写博客详细介绍。

    梯度下降法与神经网络之间有什么联系呢？

　　将复杂困难的函数当作神经网络误差，那么下山找到最小值就意味着最小化误差。这样我们就可以改进网络输出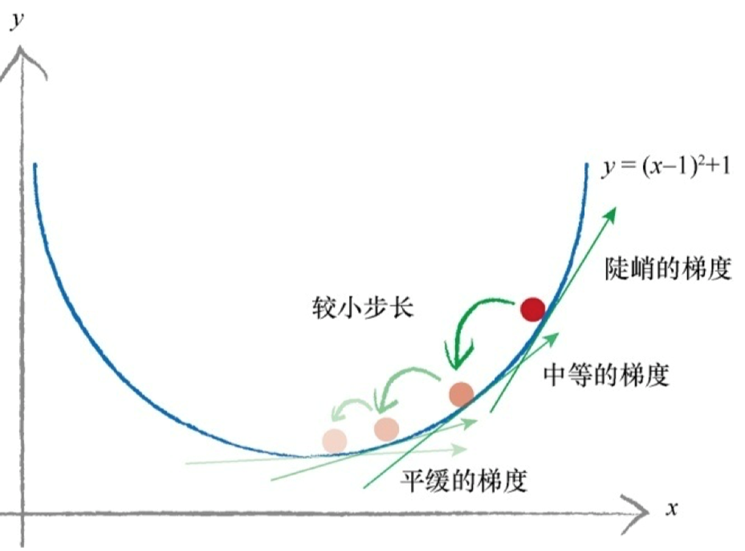       

      

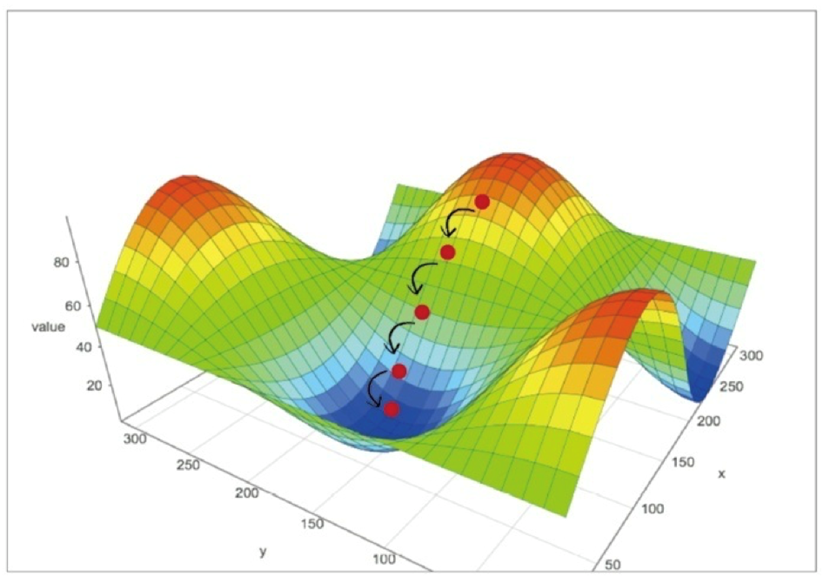
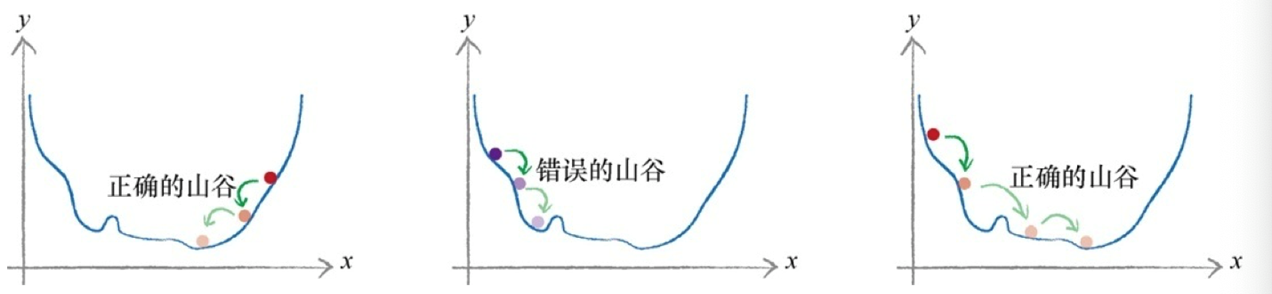
   （1）梯度下降法是求解函数最小值的一种很好的办法，当函数非常复杂困难，并且不能轻易使用数学代数求解函数时，这种方法却发挥了很好的作用；（2）更重要的是，当函数有很多参数，一些其他方法不切实际，或者会得出错误答案，这种方法依然可以适用；（3）这种方法也具有弹性，可以容忍不完善的数据，如果不能完美地描述函数，或偶尔意外地走错了一步，也不会错得离谱。

                            

                           

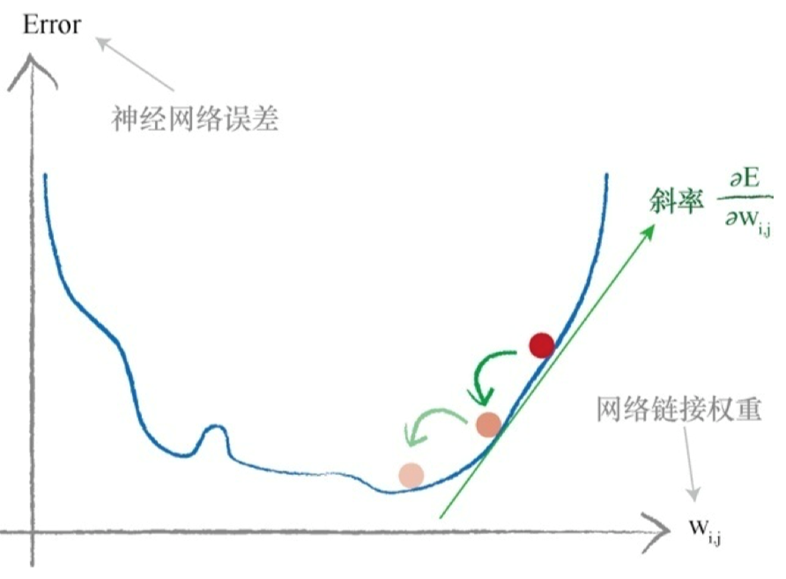
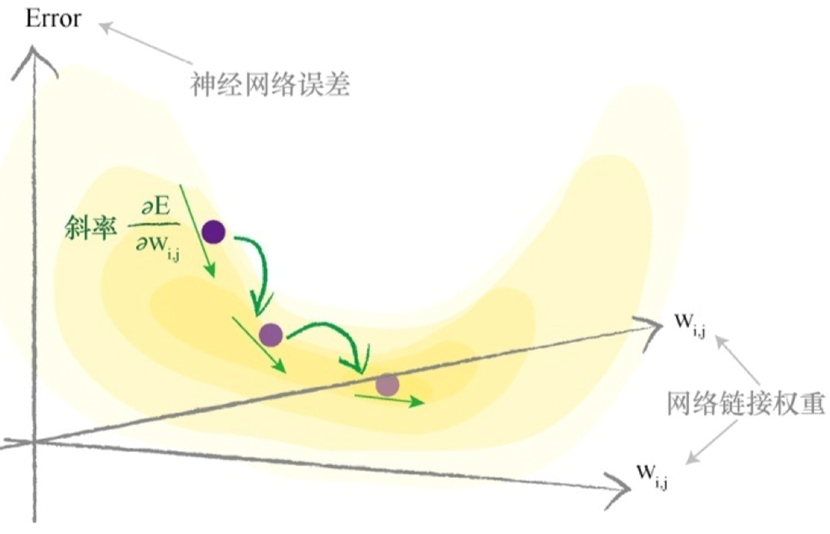
　　这个表达式表示了当权重$ w_{j,k} $改变时，误差E是如何改变的。这是误差函数的斜率，也就是希望使用梯度下降的方法到达最小值的方向。

                                              

　　误差函数推导，敲黑板，重点来了，揉揉眼睛！

       

          

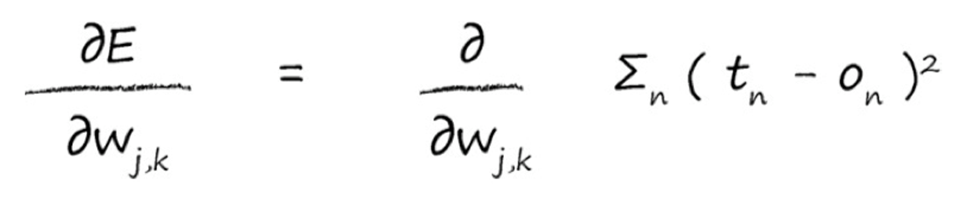
　　误差 = 目标值 - 实际值-------------$ e_k = t_k - o_k $：

         

　　借助换底技巧：

         

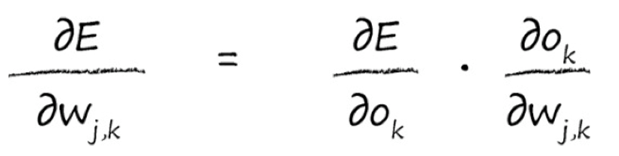
　　对$ o_k $的求导，我们可以求出来：

      

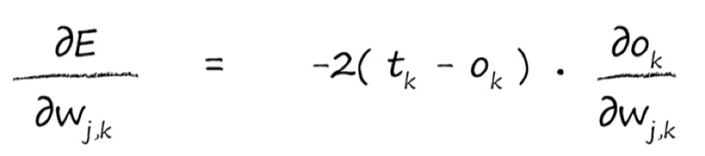
 　　j第二层，k第三层，$ o_k $即第二层的output值，应该为权重$ w_{j,k} * o_j$ ：

       

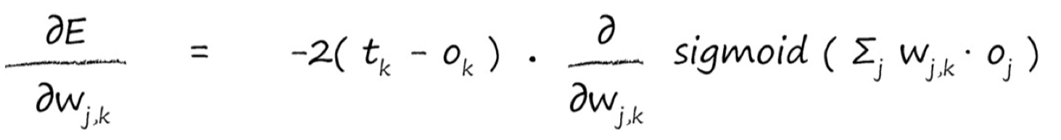
 　　对于sigmoid()函数的求导，求导结果为下式，期间的求导推导，可以自己算，也可以直接记住结果：

         

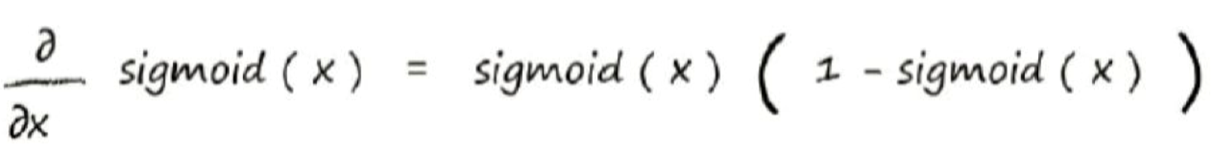
 　　知道了sigmoid函数求导结果，便可带入上式中，把x 替换成$ sum_jW_{j,k}o_j$，因为这一块与x无关，相当于常数，所以可以直接替换。

       

 　　后面那一块，就上下抵消为$ o_j $，此时式子简化成：

       

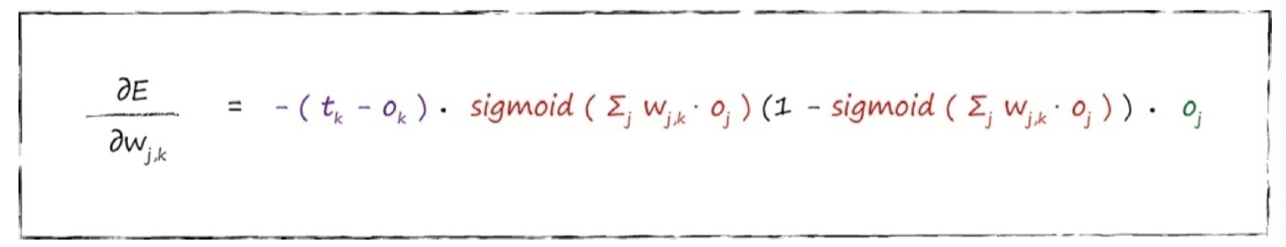
　　j第二层，k第三层：

         

 　　根据上式，与之匹配的矩阵运算如下：

      

            

　　其中a为learning rate，公式可以被简化为：

          

　　（1）神经网络的误差是内部链接权重的函数;改进神经网络，意味着通过改变权重减少这种误差；（2）直接选择合适的权重太难了。另一种方法是，通过误差函数的梯度下降，采取小步长，迭代地改进权重。所迈出的每一步的方向都是在当前位置向下斜率最大的方向，这就是所谓的梯度下降;使用微积分可以很容易地计算出误差斜率

            

          

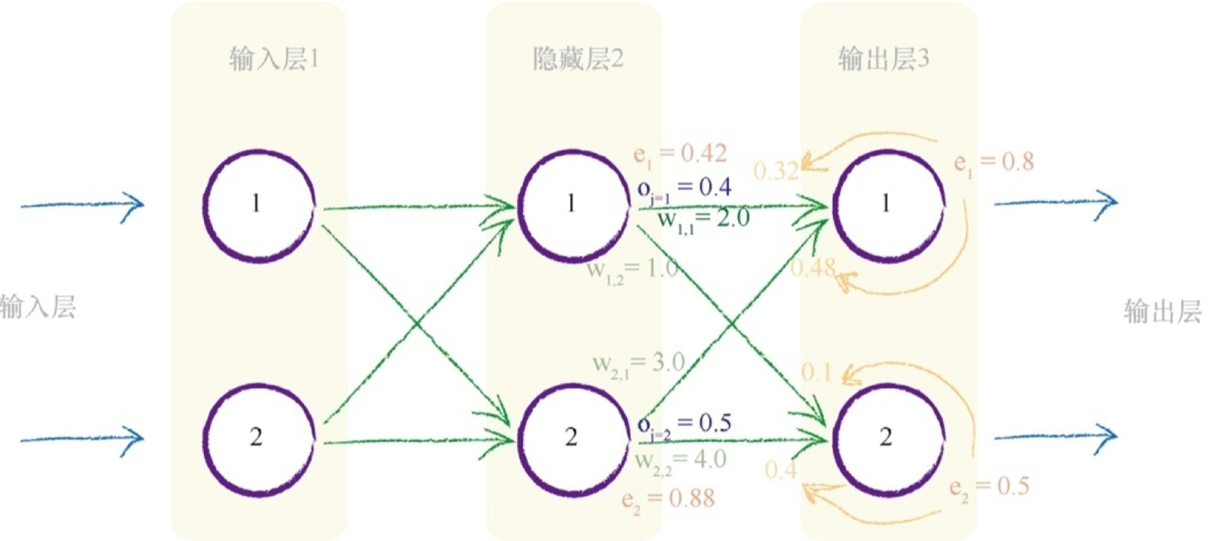
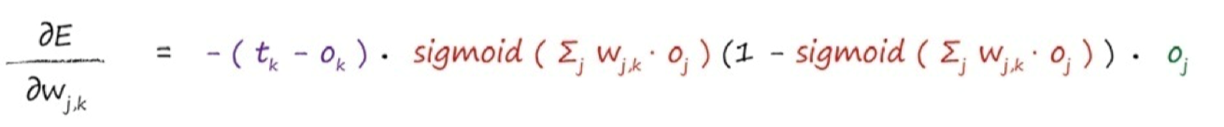
　　j第二层，k第三层-------第一项（t_k - o_k ）得到误差e_1 = 0.8。S函数内的求和$ Σ _j  w_{j,k}$，$ o_j $为（2.0×0.4）+（3.0 * 0.5）= 2.3 。sigmoid 1/(1 + e -2.3 ) 为0.909。

　　中间红色标记的表达式为0.909 *（1-0.909）=0.083。

　　由于感兴趣的是权重$ w _{1,1} $，其中j=1，因此最后一项o j 也很简单， 也就是$o_j $，j= 1 。此处，$o_j $值就是0.4。将这三项相乘，同时不要忘记表达式前的负号，最后得 到-0.0265。如果学习率为0.1，那么得出的改变量为- （0.1 * -0.02650）= +0.002650。因此，新的$ w_{1,1} $就是原来的2.0加上0.00265等于2.00265。

Neural Network 代码实现

　　概念介绍完了，下面代码实现一下，这里采用的数据集是mnist

         

import numpy as np
import scipy.special
import matplotlib.pyplot

class NeuralNetwork:
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
        self.inodes = inputnodes
        self.hnodes = hiddennodes
        self.onodes = outputnodes
        self.lr = learningrate
        
        #self.wih = np.random.rand(hnodes, inodes) - 0.5 #权重初始化
        #self.who = np.random.rand(onodes, hnodes) - 0.5 #权重初始原则和经验参考本文末尾部分
        self.wih = np.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
        self.who = np.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
        
        self.activation_fun = lambda x: scipy.special.expit(x)
        
    def train(self, input_list, targets_list):
        inputs = np.array(input_list, ndmin=2).T
        targets = np.array(targets_list, ndmin=2).T
        
        hidden_inputs = np.dot(self.wih, inputs)
        
        hidden_outputs = self.activation_fun(hidden_inputs)
        
        final_inputs = np.dot(self.who, hidden_outputs)
        
        final_outputs = self.activation_fun( final_inputs)
        
        output_errors = targets - final_outputs

        hidden_errors = np.dot(self.who.T, output_errors)
        # 权重更新
        self.who += self.lr * np.dot(output_errors * final_outputs * (1.0-final_outputs), np.transpose(hidden_outputs) )
        
        self.wih += self.lr * np.dot(hidden_errors * hidden_outputs * (1.0-hidden_outputs), np.transpose(inputs) )


    
    
    def query(self,inputs_vector):
        hidden_inputs = np.dot(self.wih, inputs_vector)
        
        hidden_outputs = self.activation_fun(hidden_inputs)
        
        final_inputs = np.dot(self.who, hidden_outputs)
        
        final_outputs = self.activation_fun( final_inputs)
        
        return final_outputs


def read_csv(filename):
    data = open(filename, "r")
    data_list = data.readlines()
    data.close()
    return data_list


def modelTrain(filename, net):
    data_list = read_csv(filename)
    ecoph = 2
    for e in range(ecoph):
        for record in data_list:
            all_value = record.split(',')
            #image_aaray = np.asfarray(all_value[1:]).reshape[28, 28]
            #pyplot.imshow(image_array, cmap="Greys", interpolation="None")
            #pyplot.show()

            inputs = np.asfarray(all_value[1:])/255 * 0.99 + 0.01
            onodes = 10
            targets = np.zeros(onodes) + 0.01
            #targets[5] = 0.99
            targets[int(all_value[0])] = 0.99

            net.train(inputs, targets)

def modelTest(filename, net):
    test_data_list = read_csv(filename)
    scorecard = []
    for record in test_data_list:
        all_value = record.split(',')
        inputs = np.asfarray(all_value[1:])/255 * 0.99 + 0.01
        outputs = net.query(inputs)
        label = np.argmax(outputs)
        correct_label = int(all_value[0])
        if correct_label == label:
            scorecard.append(1)
        else:
            scorecard.append(0)
    arr = np.asarray(scorecard)
    print("performance=", arr.sum()/arr.size)


if __name__ == '__main__':
    input_nodes = 784 #28*28
    output_nodes = 10
    hidden_nodes = 100
    lr = 0.3
    net = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, lr)
    trainFileName = "/home/xpk/xpk/Documents/zhappy/shuzishibie/mnist_train.csv"
    testFileName = "/home/xpk/xpk/Documents/zhappy/shuzishibie/mnist_test.csv"

    modelTrain(trainFileName, net)
    modelTest(testFileName, net)

　　权重知识补充：

　　小梯度意味着限制神经网络学习的能力：饱和神经网络

      

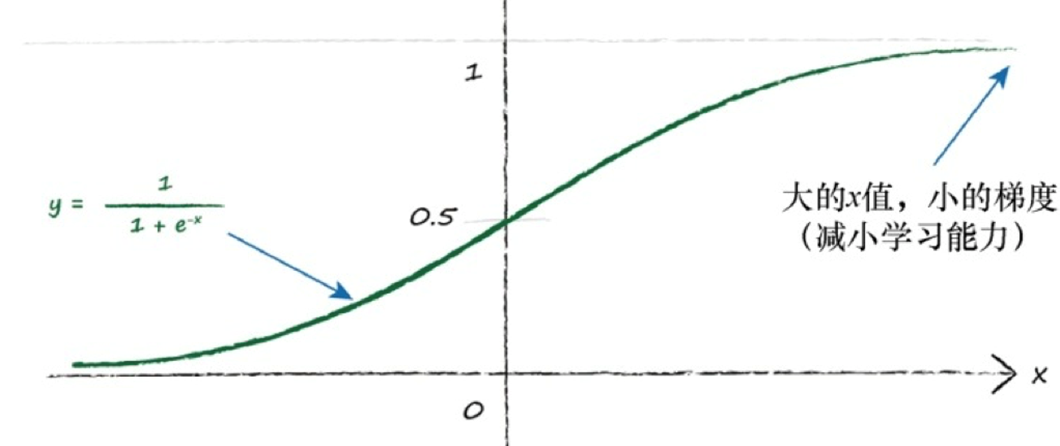
　　应该重新调整目标值，匹配激活函数的可能输出，注意避开激活函数不可能达到的值：

      

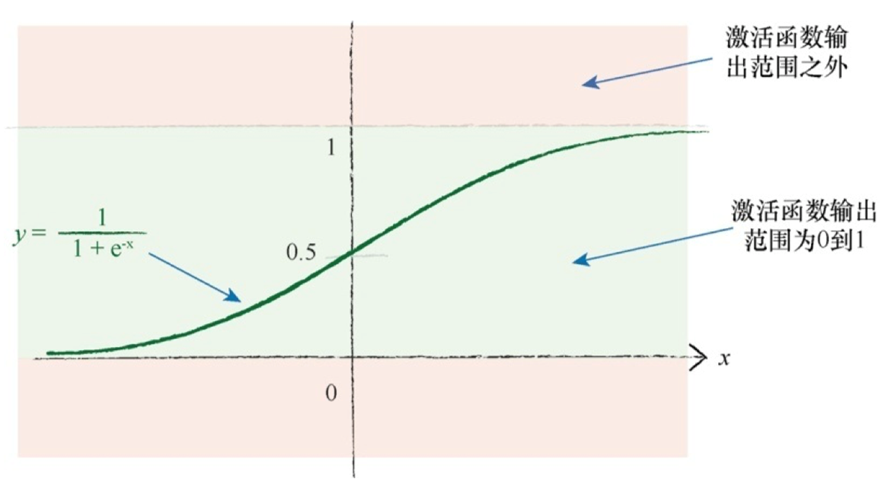
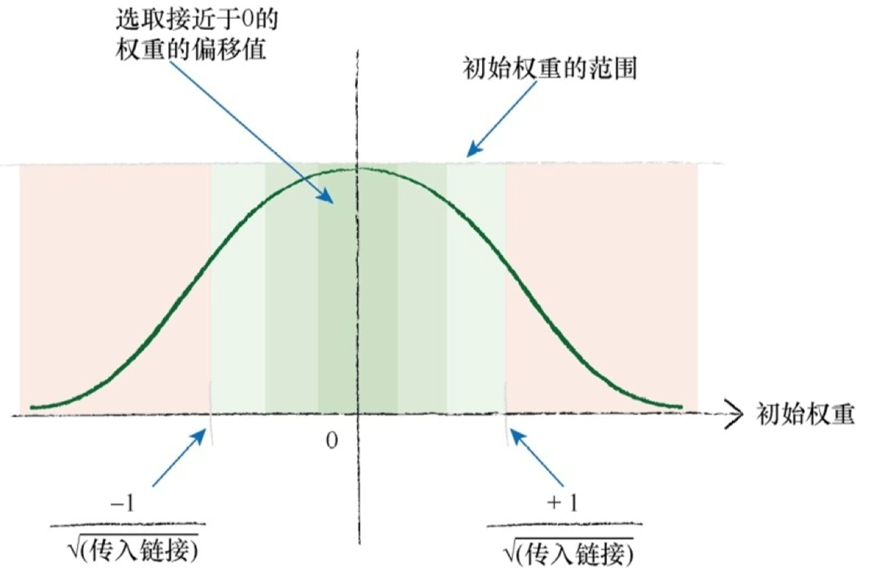
　　随机权重：（1）大的初始权重会造成大的信号传递给激活函数，导致网络饱和，从而降低网络学习到更好的权重的能力，因此应该避免大的初始权重值；（2）不希望权重破坏了精心调整输入信号的努力；（3）可以在一个节点传入链接数量平方根倒数的大致范围内 随机采样，初始化权重；

　　一些过大的初始权重将会在偏置方向上偏置激活函数，非常大的权重将会使激活函数饱和。一个节点的传入链接越多，就有越多的信号被叠加在一起。因此，如果链接更多，那么减小权重的范围，这个经验法则是有道理的

                

 　　总结：

   （1）如果输入、输出和初始权重数据的准备与网络设计和实际求解的问题不匹配，那么神经网络并不能很好地工作；

　（2）一个常见的问题是饱和。在这个时候，大信号（这有时候是由大权重带来的）导致了应用在信号上的激活函数的斜率变得非常平缓。这降低了神经网络学习到更好权重的能力；

　（3）另一个问题是零值信号或零值权重。这也可以使网络丧失学习更好权重的能力；

    （4）内部链接的权重应该是随机的，值较小，但要避免零值。如果节点的传入链接较多，有一 些人会使用相对复杂的规则，如减小这些权重的大小；

    （5）输入应该调整到较小值，但不能为零。一个常见的范围为0.01～0.99，或-1.0～1.0，使用哪个范围，取决于是否匹配了问题；

    （6）输出应该在激活函数能够生成的值的范围内。逻辑S函数是不可能生成小于等于0或大于等 于1的值。将训练目标值设置在有效的范围之外，将会驱使产生越来越大的权重，导致网络饱和。一个合适的范围为0.01～0.99。