题目:路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8 10 / 5 -3 / 3 2 11 / 3 -2 1 返回 3。和等于 8 的路径有: 1. 5 -> 3 2. 5 -> 2 -> 1 3. -3 -> 11
分析一:
求的是路径和等于目标数的路径总数量。不要求从根节点开始,也不要求到叶子节点结束。也就是说只要是路径向下的,路径中的节点值之和等于目标值即符合要求。那我们将二叉树分为三个部分,即根节点、左子树、右子树。求等于目标和的路径,有三种:第一种是从根节点出发求目标和;第二种是从根节点的左子节点出发求目标和;第三种是从根节点的右子节点出发求目标和,最终的结果就是这三种情况加起来。
无论从哪个节点出发求目标路径,其逻辑过程是一样的,首先必须是向下的,其次判断访问的节点值是否和当前目标值相同,如果相同,那么正好,路径数量加1,如果不相同那么路径数量保持。然后将当前目标值减去当前访问的节点值,作为当前节点的子节点访问的目标值传入到子节点递归过程去,当然,子节点的递归过程包含两个过程即左子节点和右子节点。注意的是,我们没访问一个结点,都会求在以当前这个访问节点为父节点的子树下所有符合当前目标和的路径总数,然后将其返回给上一层。每回溯一层,就相当于累加一次,最终能够求出总的路径数量。
代码:
private int totalpath = 0; public int pathSum(TreeNode root, int sum) { if (root == null){ return 0; } totalpath = traversalTree(root,sum) + pathSum(root.right,sum) + pathSum(root.left,sum); return totalpath; } private int traversalTree(TreeNode root,int sum){ if (root == null){ return 0; } int ret = 0; if (root.val == sum){ ret++; } ret += traversalTree(root.left,sum-root.val) + traversalTree(root.right,sum-root.val); return ret; }
分析二:前缀和+递归回溯
先说一下前缀和的概念,前缀和就是一个数组的某项下标之前,当然也包括此项元素的所有数组元素的和。用数学表达式进行表达就是:
设A为数组,其中的元素是ai,前缀和数组是S,其中的元素为si,那么前缀和的数学表达式就是:
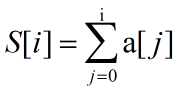
对于一组数中某两个数,如果这两个数的前缀和是相同的,那么这两个数之间的元素之和为0,通过上面的公式可以直接得出来。那么将这种思想应用到本题,假设目标和是target,在从根节点到二叉树的节点A的前缀和是curSum-target,到节点B的前缀和是curSum,(A位于B的上方)那么节点A和节点B之间的元素和就为target(组合target的元素不包含节点A的值,包含节点B的值)。
那解决这个题的办法就是,可以利用哈希表,以前缀和为key,前缀和的值为当前key的节点数量为value。每访问一个节点,就先得到当前访问节点的前缀和,然后去寻找哈希表中是否存在值为curSum-target的前缀和,如果存在那么就说明二叉树中存在路径和为目标值的路径,就将前缀和为curSum-target的节点数量(有几个前缀和为curSum的节点,就说明当前节点参与的路径和为target的路径数量有几条)加上当前节点下路径的数量。如果找不到值为curSum的前缀和,那么就将更新当前前缀和对应在哈希表中的value值,有则加1,无则初始化为1。
另外需要注意的是,该路径是有方向的,即从上到下单向进行的。所以,必须考虑回溯的问题,即我们从某个节点向上回溯的时候,需要将这个节点对应的前缀和的节点数量减去1,因为一旦回溯,肯定是回到了当前节点的上一层,那么回溯之后选择的可能是与当前节点平行的另一个子节点,而如果恢复前缀和的节点数量,那么就有可能造成从一个结点的子节点到另一个子节点的结果路径,这就不符合严格从上到下的规则,所以一旦回溯,必须恢复状态。哈希表记录前缀和的节点数量,一定是当前访问节点父亲结点及其之上的节点的情况,而不能是当前结点之下或者与其平行的节点的前缀和的情况。
代码:
public int pathSum(TreeNode root, int sum) { if (root == null){ return 0; } HashMap<Integer, Integer> map = new HashMap<>(); map.put(0,1); return traversalTree(root,0,map,sum); } private int traversalTree(TreeNode root, int curSum, Map<Integer,Integer> map,int target){ if (root == null){ return 0; } curSum += root.val; int res = 0; if (map.get(curSum-target) != null){ res += map.get(curSum - target); } if (map.get(curSum) != null){ map.put(curSum,map.get(curSum) + 1); }else { map.put(curSum,1); } res += traversalTree(root.left,curSum,map,target); res += traversalTree(root.right,curSum,map,target); map.put(curSum,map.get(curSum) - 1); return res; }