lca来啦||ヽ(* ̄▽ ̄*)ノミ|Ю!!!
开不开心qwq
这篇博客里面开头是用来给我自己复习理解用的(如果某些巨神已经会了lca也可以看一下加深一下印象),后面是我找到的一些比较好的介绍lca的博客,与君共勉(qwq其实是因为我害怕自己之后忘了lca的实现方法所以又找的博客)
对lca的理解:(lca的实现过程)
1.bfs建树:(由于要bfs 所以当然应设置一个queue啦)
1.将根节点压入queue
2.只要队列不为空,循环取出队头,判断这个点是否被访问过(因为代码中又增设了一个变量d来记录当前节点的深度,又因为除了根节点之外的所有节点的深度都被规定为0,所以只要判断这个节点的深度是否被更新过【相当于判断是否是0】,就可以判断出这个节点在之前有没有被遍历过)
3.如果访问过,跳过这个元素进行下一个节点的访问,不然更新这个接点的深度,父亲节点以及fa[][]数组
4.将当前节点压入queue
2.求x y 的 lca:
1.使x的深度小于y(因为这里是跳x)
2.使x跳到y的深度
3.如果x==y,那么表示y就是x的lca ,直接返回y的值(或者x的值)
4.否则,x和y同时向上跳,直到找到lca
5.返回y或者x(这时候他们都等于lca)的值
好啦,lca的基本实现方法就是这样滴
(*^▽^*)
下面是详细的实现方法,转自:https://www.luogu.com.cn/blog/morslin/solution-p3379
@巨神![]() MorsLin
MorsLin
LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。 ———来自百度百科
例如:
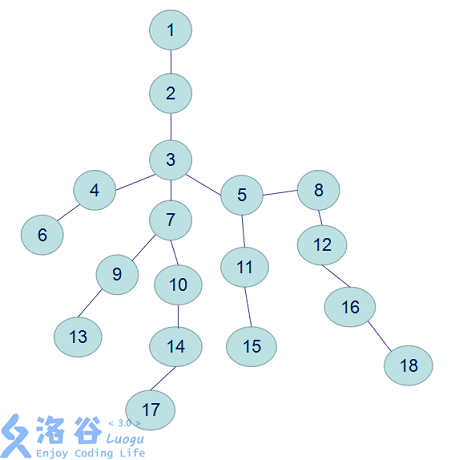
在这棵树中 17 和 8 的LCA就是 3, 9 和 7 的LCA就是 7 。
明白了LCA后,就下来我们就要探讨探讨LCA怎么求了 qwq
-
暴力算法
以 17 和 18 为例,既然要求LCA,那么我们就让他们一个一个向上爬
(我要一步一步往上爬 —— 《蜗牛》),直到相遇为止。第一次相遇即是他们的LCA。 模拟一下就是:
17−>14−>10−>7−>3
18−>16−>12−>8−>5−>3
最终结果就是 3
当然这个算法妥妥的会T飞掉,那么我们就要进行优化,于是就有了用倍增来加速的倍增LCA,这也是我们今天介绍的重点。 -
倍增算法
所谓倍增,就是按 2的倍数来增大,也就是跳 1,2,4,8,16,32不过在这我们不是按从小到大跳,而是从大向小跳,即按…… 32,16,8,4,2,1来跳,如果大的跳不过去,再把它调小。这是因为从小开始跳,可能会出现“悔棋”的现象。拿 5 为例,从小向大跳, 5≠1+2+4,所以我们还要回溯一步,然后才能得出 5=1+4;而从大向小跳,直接可以得出 5=4+1。这也可以拿二进制为例, 5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
还是以 17 和 18 为例,如果分别从 17和 18跳到 3的话,它们的路径分别是(此例只演示倍增,并不是倍增LCA算法的真正路径):
17−>3
18−>5−>3可以看出向上跳的次数大大减小。这个算法的时间复杂度为 O(nlogn),已经可以满足大部分的需求。
想要实现这个算法,首先我们要记录各个点的深度和他们 2^i级的的祖先,用数组 depth表示每个节点的深度, fa[i][j]表示节点 iii的 2^j级祖先。 代码如下:
void dfs(int now, int fath) { //now表示当前节点,fath表示它的父亲节点 fa[now][0] = fath; depth[now] = depth[fath] + 1; for(int i = 1; i <= lg[depth[now]]; ++i) fa[now][i] = fa[fa[now][i-1]][i-1]; //这个转移可以说是算法的核心之一 //意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先 //2^i = 2^(i-1) + 2^(i-1) for(int i = head[now]; i; i = e[i].nex) if(e[i].t != fath) dfs(e[i].t, now); }
预处理完毕后,我们就可以去找它的LCA了,为了让它跑得快一些,我们可以加一个常数优化(来自洛谷提高组讲义)
for(int i = 1; i <= n; ++i) //预先算出log_2(i)+1的值,用的时候直接调用就可以了 lg[i] = lg[i-1] + (1 << lg[i-1] == i); //看不懂的可以手推一下
接下来就是倍增LCA了,我们先把两个点提到同一高度,再统一开始跳。
但我们在跳的时候不能直接跳到它们的LCA,因为这可能会误判,比如 444和 888,在跳的时候,我们可能会认为 111是它们的LCA,但 111只是它们的祖先,它们的LCA其实是 333。所以我们要跳到它们LCA的下面一层,比如 444和 888,我们就跳到 444和 555,然后输出它们的父节点,这样就不会误判了。
int LCA(int x, int y) { if(depth[x] < depth[y]) //用数学语言来说就是:不妨设x的深度 >= y的深度 swap(x, y); while(depth[x] > depth[y]) x = fa[x][lg[depth[x]-depth[y]] - 1]; //先跳到同一深度 if(x == y) //如果x是y的祖先,那他们的LCA肯定就是x了 return x; for(int k = lg[depth[x]] - 1; k >= 0; --k) //不断向上跳(lg就是之前说的常数优化) if(fa[x][k] != fa[y][k]) //因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。 x = fa[x][k], y = fa[y][k]; return fa[x][0]; //返回父节点 }
完整的求 17和 18的LCA的路径:
17−>10−>7−>3
18−>16−>8−>5−>3
解释:首先, 18要跳到和 17深度相同,然后 18和 17一起向上跳,一直跳到LCA的下一层( 17是 7, 18是 5),此时LCA就是它们的父亲
总体来说就是这样了,也不知道我这个蒟蒻讲的各位 dalao能不能看明白 orz
完整代码:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; struct zzz { int t, nex; }e[500010 << 1]; int head[500010], tot; void add(int x, int y) { e[++tot].t = y; e[tot].nex = head[x]; head[x] = tot; } int depth[500001], fa[500001][22], lg[500001]; void dfs(int now, int fath) { fa[now][0] = fath; depth[now] = depth[fath] + 1; for(int i = 1; i <= lg[depth[now]]; ++i) fa[now][i] = fa[fa[now][i-1]][i-1]; for(int i = head[now]; i; i = e[i].nex) if(e[i].t != fath) dfs(e[i].t, now); } int LCA(int x, int y) { if(depth[x] < depth[y]) swap(x, y); while(depth[x] > depth[y]) x = fa[x][lg[depth[x]-depth[y]] - 1]; if(x == y) return x; for(int k = lg[depth[x]] - 1; k >= 0; --k) if(fa[x][k] != fa[y][k]) x = fa[x][k], y = fa[y][k]; return fa[x][0]; } int main() { int n, m, s; scanf("%d%d%d", &n, &m, &s); for(int i = 1; i <= n-1; ++i) { int x, y; scanf("%d%d", &x, &y); add(x, y); add(y, x); } for(int i = 1; i <= n; ++i) lg[i] = lg[i-1] + (1 << lg[i-1] == i); dfs(s, 0); for(int i = 1; i <= m; ++i) { int x, y; scanf("%d%d",&x, &y); printf("%d ", LCA(x, y)); } return 0; }
-----------题解完毕------------
-----------小蒟蒻vector代码实现----------
#include<bits/stdc++.h> using namespace std; int n,m,s,x,y,fa[5020000][25],dep[5020000]; vector<int> v[5020000]; void add(int x,int y) { v[x].push_back(y); } queue<int> q; void dfs(int p) { q.push(p); while(!q.empty()) { int x=q.front();q.pop(); for(int i=0;i<v[x].size();i++) { int y=v[x][i]; if(dep[y]) continue; dep[y]=dep[x]+1; fa[y][0]=x; for(int i=1;i<=23;i++) { fa[y][i]=fa[fa[y][i-1]][i-1]; } q.push(y); } } } int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=23;i>=0;i--) { if(dep[fa[x][i]]>=dep[y]) x=fa[x][i]; } if(x==y) return x; for(int i=23;i>=0;i--) { if(fa[x][i]!=fa[y][i]) { x=fa[x][i]; y=fa[y][i]; } } return fa[x][0]; } int main() { cin>>n>>m>>s; for(int i=1;i<=n-1;i++) { cin>>x>>y; add(x,y); add(y,x); } dep[s]=1; dfs(s); for(int i=1;i<=m;i++) { cin>>x>>y; cout<<lca(x,y)<<' '; } return 0; }