可以把任何一条从(0,0)到(n, n)的非法路径 一 一对应到一条从(0,0)到(n-1, n+1)的路径 ,因此我们所有合法路径的数量就是从(0,0)走到
(n-1, n+1)的路线的数量。
那么从(0,0)到(n - 1, n + 1)的数量有多少条呢?
从(0, 0)到(n - 1)(n +1)一共要走2n 步, 其中 向右走(n - 1)步, 向上走(n +1)步,它的方案数是C(n - 1, 2n)步,所以非法方案就是C(n - 1, 2n)。
总方案是C(n, 2n), 那么合法方案就是C(n, 2n) - C(n - 1, 2n)
合法括号序列的数量是卡特兰数, 从(0, 0)到(n, n)的合法路径的数量也是卡特兰数。还有:
举例 有一个栈, 通过这个栈对 1 ~ n排序, 那么得到的方案数也是卡特兰数:
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
这个例子可以把所有的入栈操作看作是“(”, 所有的出栈操作看作是“)”, 那么任何一个序列都对应一个合法的括号序列,也就是卡特兰数
这是第一大类的卡特兰数的情景
第二大类的卡特兰数的情景:多边形三角划分的方案数。
有一个长度为 (n + 2)的多边形;
如 : 六边形, n = 4;, 可以划分成四个三角形,划分的数量一共有多少?这也是另一种卡特兰数,是用递推的方式得到的卡特兰数。
一个边为(n + 2)的多边形,它的它划分成三角形的数量是多少呢
首先,多边形里每一条边最终一定会属于某个三角形,对吧?
因此, 我们可以把这(n + 2)条边划分为k类,枚举一下三角形的形状,一共得到n类
抽屉原理

那么他至少一共下了77盘棋,最多132盘棋
假设美天下的棋的数量分别是a1、a2、……a~77
前缀和:
s1 = a1
s1 =a1 + a2
s1 =a1 + a2 + a1
……
sn =a1 + a2 + …… + an
让所有s都加上21,得到a1+21 、 s2+21 、 ……s77+21
s77+21 <= 153
一共有154个数,153个抽屉,
那么一定有某个数出现了两次,因为每周至少一盘棋,那么s中某一个数是s+21中某一个数
相同的某个数一定是si = sj+21

问题转化为 滑动窗口,即 无论怎么排, 总有一个窗口里的数之和为9,求n的最小值为多少
证明:n最小取多少,可以使得其中必有一个si=sj+ 9、
也就是前缀和s里面保证有两个数和为0
因此,可以把所有差是9的数放到一个抽屉里面
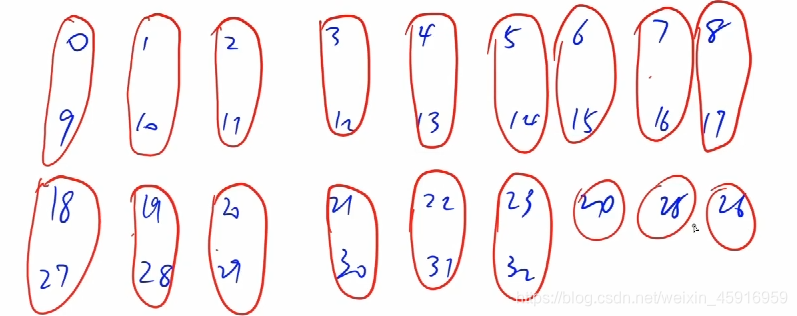
这时, 每个圈至多选择1个数,就有18个,那么再多选一个,就会一定有一个si是sj+ 0,所以19个数的话,n=18;
Nim 游戏

如果n是(m+1)的倍数,先手不管取多少,后手都区(m+1-x)这样就可以控制剩下的数量(m+1)的倍数,这样先手必败
如果 n不是(m+1)的倍数,那么先手必胜