1. 递归与分治
1.1 递归
递去，归来。
-
能够用递归解决的问题需要满足三个条件：
-
原问题可以转换为一个或多个子问题来求解，而这些子问题的求解方法和原问题完全相同，只是规模不同；
-
递归调用次数必须是有限的；
-
必须有结束递归的条件（递归出口）来终止递归。
-
-
何时使用递归：
-
定义是递归的（斐波那契）；
-
数据结构是递归的（二叉树、链表）；
-
问题求解的方法是递归的。
-
-
递归转非递归：
-
通常，尾递归可以转换为等价的非递归算法。
-
对于非尾递归的情况，可以在理解递归的实现的基础上 使用栈来模拟（二叉树非递归遍历）。
-
-
设计递归算法：
-
先求解问题的递归模型。
-
在设计递归算法的时候，如果纠结递归树的每一个阶段的话，就会极为复杂。因此，只考虑递归树中的第一层和第二层之间的关系即可，即“大问题” 和 “小问题” 的关系，其他关系类似。
-
求解问题的递归模型：
-
对原问题
f(n)进行分析，假设出合理的小问题f(n-1)； -
假设小问题
f(n-1)是可解的，在此基础上确定大问题f(n)的解，即给出f(n)与f(n-1)之间的关系，也就是确定了递归体。（与数学归纳法中确定i=n-1时成立，再求证i=n时等式成立的过程相似）。还要明确需要返回什么信息给上一层递归调用。 -
确定一个特定情况（如
f(0)或f(1)）的解，由此作为递归出口。（与数学归纳法中求证i=0或i=1时等式成立相似）
-
-
如，求数组中最小值：
#可转换为：当前元素 和 它前面所有元素中的最小值 相比较，这是一个递归的问题。 def Min(arr:list): if len(arr) <= 1: #递归出口：只含有一个元素，即认为最小（特定问题的解） return arr[0] m = Min(arr[:-1]) #假设f(n-1)是可解的，即求出来了arr[:-1]中的最小值 if m < arr[-1]: #然后将最后一个元素与“假设存在的”最小值比较 return m else: return arr[-1]
-
1.2 分治法
分治法就是：把一个复杂的问题 分解成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的 直接求解 （各个击破），原问题的解即 子问题的解的合并。
-
因此分治法的步骤为：
-
第一步 分： 将原来复杂的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题，分解到可以直接求解为止。
-
第二步 治： 此时可以直接求解。
-
第三步 合： 将小规模的问题的解合并为一个更大规模的问题的解，自底向上 逐步求出原来问题的解。
-
-
算法的设计模式：
Divide_and_Conquer(P){ if(xxx) //递归出口：如果规模足够小，克制直接求解，则开始“治” return ADHOC(P); //ADHOC是治理可直接求解子问题的子过程 <divide P into smaller subinstances P1,P2,...Pk>; //将P“分”解为k个子问题 for(int i = 0; i < k; ++i) yi = Divide_and_Conquer(Pi); //递归求解各个子问题 return merge(y1, y2, ..., yk); //将各个子问题的解“合”并为原问题的解 } -
设计划分策略，把原问题P分解成K个规模较小的子问题，这个步骤是分支算法的基础和关键。需要遵循两个原则：
-
平衡子问题原则：分解出的k个子问题规模最好大致相当；
-
独立子问题原则：分解出的k个子问题之间重叠越少越好，最好k个子问题相互独立，不存在重叠子问题。
-
-
分治法的复杂度分析（主定理）：
-
有递推关系式
T(n) = aT(n/b) + f(n)，其中n为问题规模，a为递推的子问题数量，n/b 为子问题的规模（假设每个子问题的规模都一样），f(n) 为递推以外进行的计算工作， a>=1, b>=1 是常数。则：-
若对于常数ε >0，有 f(n) = O(nlogb(a)-ε) ，ε > 0，则 T(n) = Θ(nlogba) ；（O(xxx)是f(n)的上界，T(n)的渐进阶为较大的那个，较大的就是 nlogba，因此T(n)就等于它）
-
若 f(n) = θ(nlogba) ，则 T(n) = Θ(nlogba·logn) （小θ表示同阶）
-
若常数 ε > 0，有 f(n) = Ω(nlogb(a)+ε) ，且对于某常数 c > 1 和所有充分大的额正整数n有
af(n/b) <= cf(n)，则 T(n) = Θ(f(n)) 。（Ω(xxx)是f(n)的下界，T(n)的渐进阶为较大的那个，较大的就是f(n)，因此T(n)就等于它）
-
-
例1：
-
求 T(n) = 9T(n/3) + n 渐进阶(Θ) :
-
a = 9, b = 3, f(n) = n; n^(logba) = n^2; 取 ε = 0.1 ，f(n) = O(nlogb(a) - ε) = O(n^1.9)，因此 T(n) = Θ(n^2)
-
-
例2：
-
T(n) = T(2n/3) + 1
-
a = 1, b = 3/2, f(n) = 1, n^(logba) = n^0 = 1, f(n) = 1, f(n) 与 n^(logba) 同阶，则 T(n) = Θ(logn)
-
-
例3：
-
T(n) = 2T(n/2) + nlogn
-
a = 2, b= 2, f(n) = nlogn, n^(logba) = n^1 = n, f(n) = nlogn，n^(logba) 是 f(n) 的下限，但不满足 f(n) = Ω(nlogb(a)+ε) ，因此无法应用Master定理。
-
-
-
例：分治 - 求和
def sum(arr:list): if len(arr) == 1: return arr #“治” 直接求解 mid = len(arr)//2 l = arr[:mid] r = arr[mid:] #“分” 分解成两个子问题 return sum(l) + sum(r) #“合” 自底向上求子数组l和r的和 sum([1,2,3,4]) #10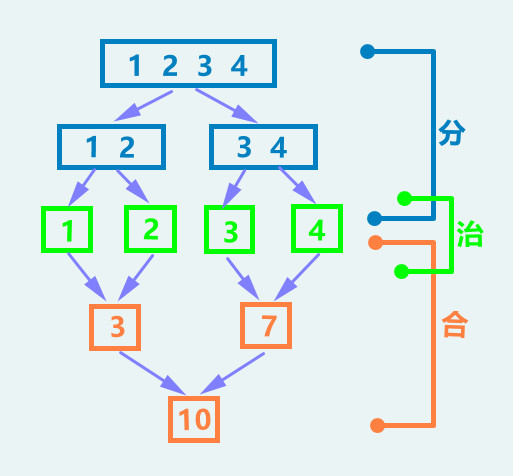
-
例：分治 - 归并排序
对于一个含有很多元素的数组，直接排序不容易，但如果分解成多个规模很小的数组（只有一个元素），那么这时候两个子数组排序（归并）就很容易了。
def merge(arr:list, low:int, mid:int, high:int): l = arr[low:mid] r = arr[mid:high] i = j = 0 # 用于迭代子序列l、r k = low len_l = mid-low len_r = high-mid while i < len_l or j < len_r: if j == len_r or (i < len_l and l[i] <= r[j]): arr[k] = l[i] k += 1 i += 1 else: arr[k] = r[j] k += 1 j += 1 def mergeSort(arr:list, low:int, high:int): if high-low == 1: #一个元素本身已经有序 return arr #“治” 直接求解 mid = (high+low) // 2 mergeSort(arr, low, mid) mergeSort(arr, mid, high) #“分” 分解成两个子问题 merge(arr, low, mid, high) #“合” 自底向上归并两个有序子数组 arr = [3,1,2,4,5] mergeSort(arr, 0, len(arr)) #[1,2,3,4,5]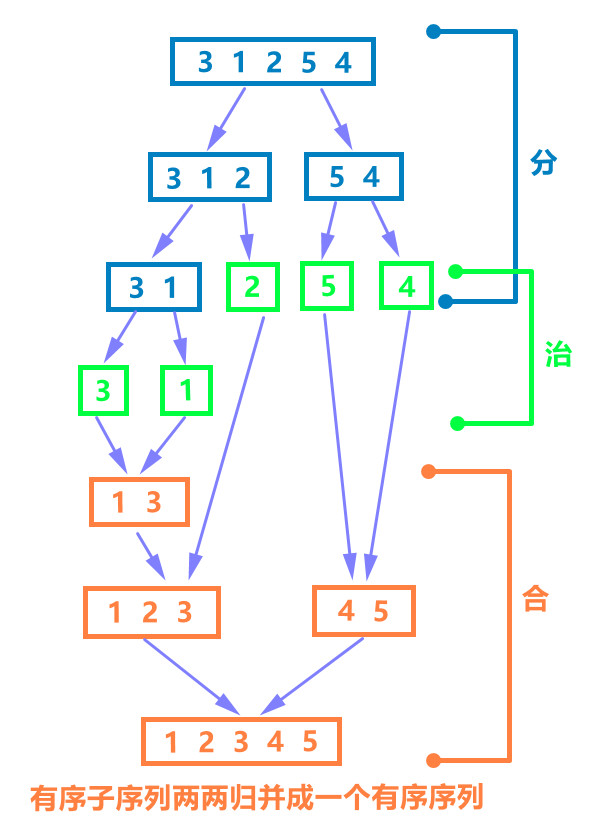
-
例：分治 - 求逆序对数目
-
如，
{3, 1, 2, 4}中逆序对有<3,1> <3,2> -
如果枚举的话，时间复杂度是O(n^2)。可以借用归并排序（O(nlogn)）。
-
如果数组只有一个元素，逆序对为0；
-
原数组A中逆序对可以分为三个部分：第一部分为子数组A1中的逆序对数C1；第二部分为A2中的C2；第三部分是一个元素在A1，而另一个元素在A2，这两个元素构成一个逆序对，C3。
-
对于C3，可以借助归并的过程判断。
-
def merge(arr:list, low:int, mid:int, high:int): num = 0 #逆序对数 l = arr[low:mid] r = arr[mid:high] i = j = 0 # 用于迭代子序列l、r k = low len_l = mid-low len_r = high-mid while i < len_l or j < len_r: if j == len_r or (i < len_l and l[i] <= r[j]): arr[k] = l[i] k, i = k + 1, i + 1 else: arr[k] = r[j] k, j = k + 1, j + 1 if i != len_l: #判断是因为，当i==len_l时，就会多加 num += 1 #【如果 l[i] < r[j] 则存在逆序对】 return num def mergeSort(arr:list, low:int, high:int): if high-low == 1: #一个元素本身已经有序 return 0 #“治” 直接求解，只含有一个元素的数组的逆序对的数目为0 mid = (high+low) // 2 C1 = mergeSort(arr, low, mid) C2 = mergeSort(arr, mid, high) #“分” 分解成两个子问题 C3 = merge(arr, low, mid, high) #“合” 自底向上归并两个有序子数组 return C1 + C2 + C3 arr = [3,1,2,4,5] mergeSort(arr, 0, len(arr)) #3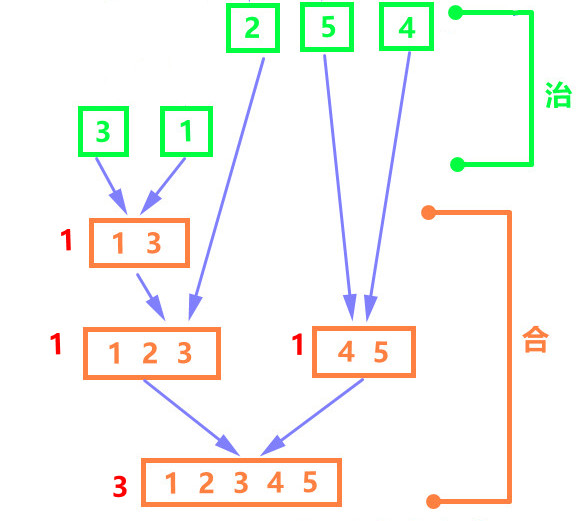
-
-
例：分治 - 快速排序
思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
-
过程：
-
分： 对于一个整数集合
A = {a[l], ..., a[r]}，以 a[l] 为基准将A划分为三个部分：A1、A2、A3，其中A2 = {a[l]}，A1所有元素都小于等于A2，A3所有元素都小于A1。然后分别对A1、A3进行递归处理，从而使得整个集合有序。 -
治： 如果划分后的A1和A3只含有一个元素，则已经有序，直接返回即可。
-
合： 因为在分的过程中A1和A3已经排好序了，所以A1、A2和A3已经有序了，在合并阶段无需处理。
-
def partition(arr:list, low:int, high:int): base = arr[low] # 备份基准元素，现在arr[low]空出来了 while low < high: while (low < high) and (arr[high] > base): #从右至左找到一个比基准元素小的 high -= 1 arr[low] = arr[high] #arr[low]已经空出，将比基准元素小的arr[high]填入空出的位置，然后arr[high]空出 while (low < high) and (arr[low] <= base): #从左至右找到一个比基准元素大的 low += 1 arr[high] = arr[low] #arr[high]已经空出，将比基准元素大的arr[low]填入空出的位置，然后arr[low]空出 arr[low] = base #while终止时 high==low，最后终止的位置，一定是high或low空出的（因为内while终止时，是被另一个位置拿走一个值，然后空出），所以可以直接将基准元素填入 return high def quickSort(arr:list, low:int, high:int): if low < high: k = partition(arr, low, high) quickSort(arr, low, k - 1) quickSort(arr, k + 1, high) ### === 其他划分思路 === ### 双路快排【困扰了半个月】 def partition(arr, l, r): base = arr[l] ll = l #l += 1 #不能加！加了之后只有两个元素的情况无法进入循环。如以下两种： # [1,2] # [2,1] while l < r: while l < r and arr[r] > base: #必须从右端开始，因为只有这样，循环因为l<r的条件不符合时终止的位置的元素才能比base小。如果先从左端开始的话，最后l==r，r此时指向的元素极有可能大于base，因此最后交换的话，比base大的值会放到base的左边。如[3,4,2,1,5]画图可看出。 r -= 1 while l < r and arr[l] <= base: l += 1 arr[l], arr[r] = arr[r], arr[l] arr[ll], arr[r] = arr[r], arr[ll] return r ### ll+1 ~ l 是小于base的区域 def pt(arr, l, r): ll = l base = arr[l] for i in range(ll+1, r+1): if arr[i] < base: l += 1 arr[l], arr[i] = arr[i], arr[l] arr[ll], arr[l] = arr[l], arr[ll] return l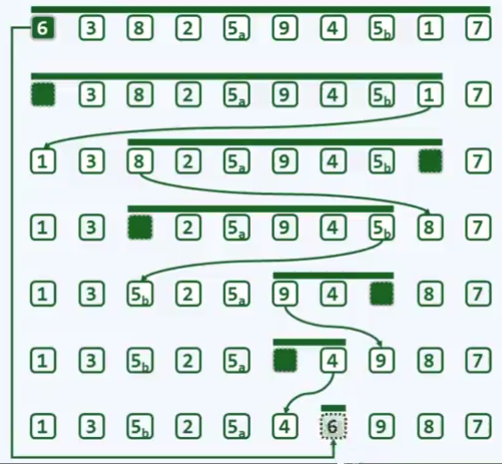
（图：学堂在线邓俊辉的老师MOOC ） -
-
性能分析：
-
不稳定排序：因为low和high移动方向相反，左右侧的相同大小的元素可能颠倒。
-
就地（空间复杂度O(1)）。
-
最好情况时间复杂度：每次划分都（接近）平均，轴点总是（接近）中点；复杂度为
T(n) = 2·T((n-1)/2) + O(n) = O(nlogn)(减一是中间的轴点没包括)。 -
最坏情况：每次划分都极不均衡，复杂度为
T(n) = T(n-1) + T(0) + O(n) = O(n^2)。 -
平均情况：
O(nlogn)。
-