上午
(cjh)学长讲课了,主要讲的动规
1.线性dp
典型例题
不会这个题(....!!!!!!)
四个(if)四个(for) 注意计数器从(0)还是(1)开始的
2.背包(他没讲)
3.区间dp
典型例题
两个题几乎都一样
给出区间dp的板子:
初始化balbalbala.....
for (int len = 2; len <= n; ++ len)
for (int i = 1; i <= n-len+1; ++ i) {
int j = i+len-1;
for (int k = i; k < j; ++ k)
f[i][j] = max/min(f[i][j],f[i][k]+f[k+1][j]*sth..)
}
其中
(f[i][j] = max/min(f[i][j], f[i][k]+f[k+1][j]*sth..))
4.状压dp
典型例题
学长说题解第一种做法不太好
最好是枚举子集 那样比较好
PS
枚举子集
int S = 233333;
for (int i = S; i; i = (i-1)&S)
cout <<bitset<10>(i)<<'
';
还有比较操蛋的插头dp
甩个比较好的链接
讲了到题 铺地板
对于此题 我们枚举三个状态,但是这个题有点难,对于我这种初学者不太合适
我们考虑一种简单的题:
还是铺地板,不过没有障碍物,我们铺的都是直线,并且,直线都是长至少为2,宽固定为1
对于这个题 我们规定 能继续延伸无论是横着或者竖着都是1
如果不能继续延伸 规定为0
然后每一行都是(2^{n}),有(n)行,所以复杂度为(n*2^{n})
5.期望dp(他没讲)
6.树形dp(他说是重点)
前两个题目都差不多,主要是我们开个(f)数组,(0)表示这个点没来(或者是不选),(1)表示来(或者是选):(f[i][0/1])
然后我们就可以根据他们的儿子来转移
对于上面那道题
(f[i][0] = sum{max(f[son][0], f[son][1])})
(f[i][1] = sum{f[son][0]}+v[i])
其中(v[i])表示(i)这个节点的快乐指数
对于下面那道题
(f[i][0] += f[son][1])
(f[i][1] += min(f[son][0], f[son][1]))
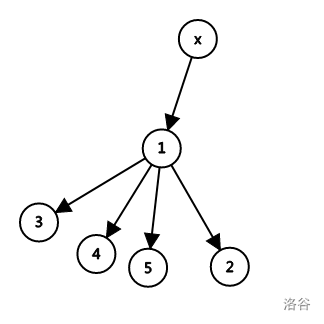
如图,我们假设节点(1)的下面有(k)个黑点,(x-->1)这条边为(val)
我们考虑(val)对整个图形的影响
设一共有(B)个黑点,(W)个白点
顾(val)对整个图形的影响为:
((k*(B-k)+(s[1]-k)*(w-(s[1]-k))*val)
其中(s[1])表示以(1)为祖先的子树的大小((size))
下午
一开始讲了一会,后来就做题了
讲了一个虚树
还有两个动规优化
对于玩玩具的那个:
-
1找出(dp)式子
-
2魔改
-
3运用线性规划的知识与凸包的知识
-
4用斜率优化来做他
对于玩股票的那个:
我们设(f[i][j])在第(i)天有(j)支股票能获得的最大价值
- 1 凭空买
(f[i][j] = -ap_{i}*j) 其中((0leq j leq as_{i}))
- 2 不买也不买
(f[i][j] = max(f[i-1][j], f[i][j])
- 3 在之前的基础上买
(f[i][j] = max(f[i][j], f[i-(w+1)][k]-(j-k)*ap{i})
其中((j-as_{i}leq k <j))
- 4在之前的基础上卖
(f[i][j] = max(f[i][j], f[i-(w+1)][k]+(k-j)*bp_{i})
其中((j<k leq j+bs_{i}))
然后经过一系列(nb)操作就可以用单调队列来优化了...
但是我既不会写代码也不会写优化
连这些状态都是从题解看过来的
晚上
关于插头(dp)上午说的那个简单例题,学长给出了代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long int64;
const int64 p = 1e9 + 7;
void work(int n, int m)
{
unordered_map<int, int64> dp[2];
int numnow = 0, numnext = 1;
dp[numnow][0] = 1;
for(int line = 1; line <= n; ++line)
{
for(int i = 1; i <= m; ++i)
{
dp[numnext].clear();
for(auto s = dp[numnow].begin(); s != dp[numnow].end(); ++s)
{
int nowst = s->first, nowval = s->second;
int u = (nowst >> i) & 1, l = (nowst >> (i - 1)) & 1;
if(u == 0 && l == 0)
{
(dp[numnext][nowst ^ (1 << i)] += nowval) %= p;
(dp[numnext][nowst ^ (1 << (i - 1))] += nowval) %= p;
}
if(u == 1 && l == 0)
{
(dp[numnext][nowst ^ (1 << i)] += nowval) %= p;
(dp[numnext][nowst ^ (1 << i) ^ (1 << (i - 1))] += nowval) %= p;
}
if(u == 0 && l == 1)
{
(dp[numnext][nowst ^ (1 << (i - 1))] += nowval) %= p;
(dp[numnext][nowst ^ (1 << i) ^ (1 << (i - 1))] += nowval) %= p;
}
}
swap(numnow, numnext);
}
dp[numnext].clear();
for(auto s = dp[numnow].begin(); s != dp[numnow].end(); ++s)
{
if(((s->first >> m) & 1) == 0)
dp[numnext][s->first << 1] = s->second;
}
swap(numnow, numnext);
}
cout << dp[numnext][0] << endl;
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
work(n, m);
return 0;
}
对于这份代码
其中(u)为(up),(l)为(left) 分别代表上边和左边来的数字
(nowst,nowval)分别代表当前这一行的状态,当前及以前已经拥有的方案数
(从左往右更新的,因此(i)在右边,(i-1)在左边)
对于特娘的三种(if)我们来画几个图

对于这个图 我们u和l都为0也就是说,当前状态我们只能再向下或者右转移
上图是(nowst)^(1<<(i-1))的情况 即向下开始直线
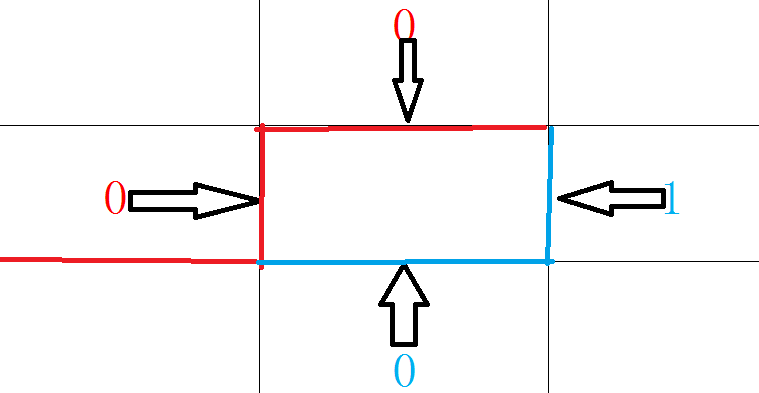
向右延伸的直线,即(nowst)^(1<<i)
至此(u = 0, l = 0)的情况结束。来看(u = 1, l = 0)的情况!
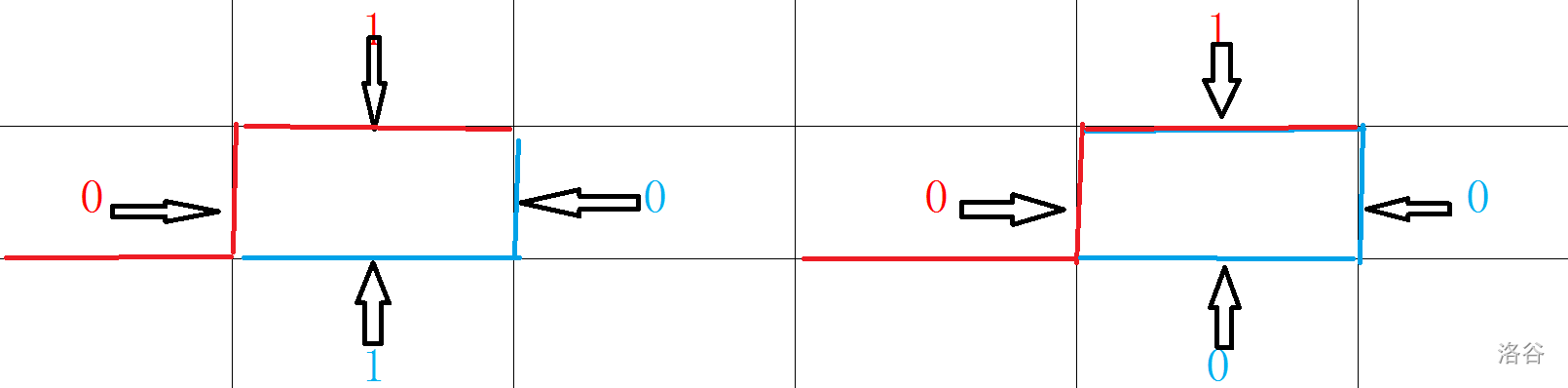
当(nowst)异或两次,即把第(i)位与第((i-1))位都取反了
对于取反两次的情况,就是顺着原来的方向走,原来是竖着,现在还是竖着
而上图右边的那个情况是 (nowst)^((1<<i)),即停止下渗
至此(u = 1, l = 0)的情况结束。来看(u = 0, l = 1)的情况!
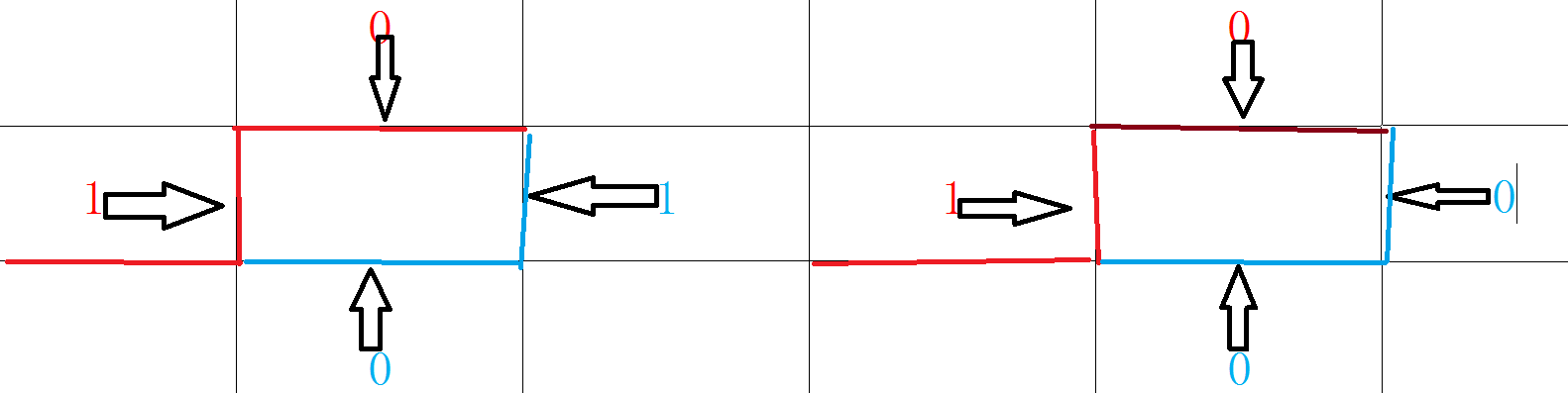
当(nowst)异或两次,即把第(i)位与第((i-1))位都取反了
对于取反两次的情况,就是顺着原来的方向走,原来是横着着,现在还是横着
而上图右边的那个情况是 (nowst)^((1<<(i-1)),即停止继续向左
(End...)