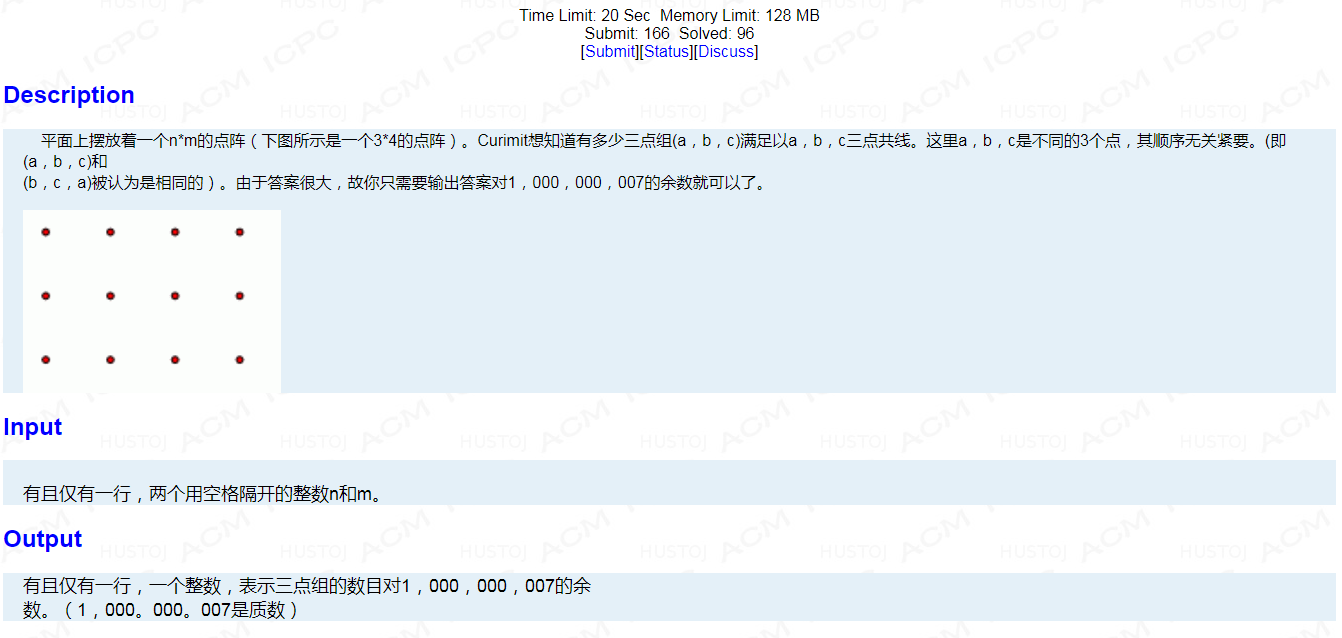

(权限题所以还是贴一下题面好了)
Solution
显然答案可以被分成两部分分别计算,一种是横的和竖的(可以直接算),另一种是斜的
考虑横的和竖的怎么算,这个直接组合数一下就好了
[ans1=mcdot C_n^3+ncdot C_m^3
]
然后斜的话,我们转成确定了第一个点和第三个点,求第二个点有多少个这样一个问题来求解
第二个点的话肯定要是整点,我们假设第一、三点的横、纵坐标之差分别为(i)和(j),那么用相似来推一下:
假设第二个点和第一个点的横、纵坐标之差分别是(x)和(y),那么
[egin{aligned}
frac{x}{i}&=frac{y}{j}\
x&=ycdot frac{i}{j}\
&=ycdot frac{i/gcd(i,j)}{j/gcd(i,j)}
end{aligned}
]
那么(y)应该要是(b/gcd(a,b))的倍数,那么(y)的取值总共有(frac{j}{j/gcd(i,j)}=gcd(i,j))种
然后去掉那个跟第三个点重合的点,第二个点总共就有(gcd(i,j)-1)种
然后根据对称性我们可以只考虑第一个点在第三个点左上角的情况,然后乘个(2)就好了
所以我们可以枚举(i,j),得出式子:
[egin{aligned}
ans2&=2sumlimits_{i=1}^{n-1}sumlimits_{j=1}^{m-1}(n-i)(m-j)(gcd(i,j)-1)\
&=2(sumlimits_{i=1}^{n-1}sumlimits_{j=1}^{m-1}(n-i)(m-j)sumlimits_{d|gcd(i,j)}varphi(d)-sumlimits_{i=1}^{n-1}sumlimits_{j=1}^{m-1}(n-i)(m-j))\
&=2(sumlimits_{d=1}^{min(n-1,m-1)}varphi(d)sumlimits_{i=1}^{lfloorfrac{n-1}{d}
floor}sumlimits_{j=1}^{lfloorfrac{m-1}{d}
floor}(n-di)(m-dj)-sumlimits_{i=1}^{n-1}sumlimits_{j=1}^{m-1}(n-i)(m-j))\
end{aligned}
]
其中第二步是用到了(sumlimits_{d|n}varphi(d)=n)的性质,然后第二步到第三步是转成枚举(gcd(i,j))(也就是(d))
(第二步那里一开始十分冲动直接上(mu)了然后发现什么都没搞出来。。。)
然后前面的(varphi)可以直接快速幂筛出来,后面的式子提一下公约数什么的可以直接用等差数列求和公式(O(1))解决
千万千万千万不要忘记了最开始的式子是(gcd(i,j)-1)而不是(gcd(i,j))。。。
最后输出(ans1+ans2)就好啦ovo
代码大概长这个样子
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MOD=1e9+7,MAXN=50010;
int phi[MAXN],p[MAXN],fac[MAXN],invfac[MAXN];
bool vis[MAXN];
int n,m,cnt,ans;
void prework(int n);
int sum(int n);
int getsum(int n,int d);
int ksm(int x,int y);
int C(int n,int m){if (n<m) return 0;return 1LL*fac[n]*invfac[m]%MOD*invfac[n-m]%MOD;}
int gcd(int x,int y){return y?gcd(y,x%y):x;}
int Sum(int n);
int main(){
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
#endif
scanf("%d%d",&n,&m);
int mn=min(n-1,m-1),mx=max(n-1,m-1);
prework(mx+1);
ans=0;
for (int d=1;d<=mn;++d)
ans=(1LL*ans+1LL*phi[d]*getsum(n,d)%MOD*getsum(m,d)%MOD)%MOD;
ans=(1LL*ans+MOD-1LL*sum(n-1)*sum(m-1)%MOD)%MOD;
ans=ans*2%MOD;
ans=(1LL*ans+(1LL*n*C(m,3)%MOD+1LL*m*C(n,3)%MOD)%MOD)%MOD;
printf("%d
",ans);
}
void prework(int n){
cnt=0;
phi[1]=1;
for (int i=2;i<=n;++i){
if (!vis[i])
phi[i]=i-1,p[++cnt]=i;
for (int j=1;j<=cnt&&p[j]*i<=n;++j){
vis[p[j]*i]=true;
if (i%p[j]==0){
phi[i*p[j]]=phi[i]*p[j];
break;
}
else
phi[i*p[j]]=phi[i]*phi[p[j]];
}
}
fac[0]=1;
for (int i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%MOD;
invfac[n]=ksm(fac[n],MOD-2);
for (int i=n-1;i>=0;--i) invfac[i]=1LL*invfac[i+1]*(i+1)%MOD;
}
int ksm(int x,int y){
int ret=1,base=x;
for (;y;y>>=1,base=1LL*base*base%MOD)
if (y&1) ret=1LL*ret*base%MOD;
return ret;
}
int sum(int n){
int tmp=n+1;
if (tmp&1) n/=2;
else tmp/=2;
return 1LL*n*tmp%MOD;
}
int getsum(int n,int d){
return (1LL*n*((n-1)/d)%MOD+MOD-sum((n-1)/d)*d%MOD)%MOD;
}