Church encoding

In mathematics, Church encoding is a means of representing data and operators in the lambda calculus. The data and operators form a mathematical structure which is embedded in the lambda calculus. The Church numerals are a representation of the natural numbers using lambda notation. The method is named for Alonzo Church, who first encoded data in the lambda calculus this way.

Terms that are usually considered primitive in other notations (such as integers, booleans, pairs, lists, and tagged unions) are mapped to higher-order functions under Church encoding. TheChurch-Turing thesis asserts that any computable operator (and its operands) can be represented under Church encoding. In the untyped lambda calculus the only primitive data type is the function. The Church-Turing thesis is that lambda calculus is Turing complete.

The Church encoding is not intended as a practical implementation of primitive data types. Its use is to show that other primitives data types are not required to represent any calculation. The completeness is representational. Additional functions are needed to translate the representation into common data types, for display to people. It is not possible in general to decide if two functions are extensionally equal due to the undecidability of equivalence from Church's theorem. The translation may apply the function in some way to retrieve the value it represents, or look up its value as a literal lambda term.

Lambda calculus is usually interpreted as using intensional equality. There are potential problems with the interpretation of results because of the difference between the intensional and extensional definition of equality.

邱奇编码是把数据和运算符嵌入到lambda演算内的一种方式，最常见的形式是邱奇数，它是使用lambda符号的自然数的表示法。这种方法得名于阿隆佐·邱奇，他首先以这种方法把数据编码到lambda演算中。

在其他符号系统中通常被认定为基本的项（比如整数、布尔值、有序对、列表和tagged unions）都被映射到使用邱奇编码的高阶函数；根据邱奇-图灵论题我们知道任何可计算的运算符（和它的运算数）都可以用邱奇编码表示。

很多学数学的学生熟悉可计算函数集合的哥德尔编号；邱奇编码是定义在lambda抽象而不是自然数上的等价运算。

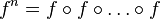Church数是在Church编码下的自然数的表示法。表示自然数 $n$ 的高阶函数是把任何其他函数 $f$ 映射到它的n重函数复合 $f^n = f circ f circ ldots circ f$ 的函数

定义

Church数0, 1, 2, ...在lambda演算中被定义如下：

0 ≡ λf.λx. x

1 ≡ λf.λx. f x

2 ≡ λf.λx. f (f x)

3 ≡ λf.λx. f (f (f x))

...

n ≡ λf.λx. fⁿ x

...

就是说，自然数 $n$ 被表示为Church数n，它对于任何lambda-项F和X有着性质：

n F X =_β Fⁿ X。

λ演算（lambda calculus）是一套用于研究函数定义、函数应用和递归的形式系统。
Lambda演算被称为最小的通用程序设计语言。它包括一条变换规则（变量替换）和一条函数定义方式，Lambda演算之通用在于，任何一个可计算函数都能用这种形式来表达和求值。因而，它是等价于图灵机的。尽管如此，Lambda演算强调的是变换规则的运用，而非实现它们的具体机器。可以认为这是一种更接近软件而非硬件的方式。

形式化定义

所有的lambda表达式可以通过下述以BNF范式表达的上下文无关文法描述：

<expr> ::= <identifier>
<expr> ::=(λ<identifier> .<expr>)
<expr> ::=(<expr> <expr>)

例如：λx y.x+y

头两条规则用来生成函数，而第三条描述了函数是如何作用在参数上的。

如下假定保证了不会产生歧义：（1）函数的作用是左结合的，和（2）lambda操作符被绑定到它后面的整个表达式。例如，表达式 (λx.x x)(λy.y) 可以简写成λ(x.x x) λy.y 。

通过lambda terms来组成
1.函数名,不重要,所以lambda演算不需要.
2.多参数的函数都可以转换为单参数的函数,所以不需要
多参数函数.
3.参数名无所谓,所以the naive notion of equality on
lambda terms is alpha-equivalence。

语法十分简单:
– lt可以是一个变量,x;
– t如果是一个lt（lambda term), x是一个变量的话, λx.t 也是一个lt( 叫做
lambda abstraction)
– 如果t和s是lt,那么ts也是( 叫做 application)
● 括号用来解决表达式上的歧义问题,比如【λ写作Y】：
– Yx.((Yx.x)x) 和 (Yx.(Yx.x))x两者不同,要是没括号就弄
不清楚了.

Alpha equivalence
● Free variables
– 没绑定的都算.Yx.x没有.Yx.y中y是.
● Capture-avoiding substitutions
– 设定 t,s,r是lt,x、y是变量的情况下, t[x:=r]的意思是将t中的x以r来替换.
– x[x:=r] = r
– y[x:=r] = y if x != y
– (ts)[x:=r] = (t[x:=r])(s[x:=r])
– (Yx.t)[x:=t] = Yx.t
– (Yy.t)[x:=r] = Yy.(t[x:=r]) if x!=y 且y 非r中的自由变量
– 示例:
● (Yx.x)[y :=y] = Yx.(x[y:=y]) = Yx.x
● ((Yx.y)x)[x:=y] = ((Yx.y)[x:=y])(x[x:=y])=(Yx.y)y

– 最后一个变化式中y非r中的自由变量的作用在于避免变换过程中出现
歧义,避免歧义的方法就是修改变量名称就可以.
● (Yx.y)[y:=x]=Yx.(y[y:=x])=Yx.x 有歧义
– 修改名称后:
● (Yz.x)[x:=y]=Yz.(x[x:=y])=Yz.y 无歧义
● Beta reduction
– (Yx.t)s可以转化成 t[x:=s]
– 其实应该就是求值的过程:
● (Yx.xx)(Yx.xx)
-> (Yx.xx)[x:=Yx.xx] = (x[x:=Yx.xx])(x[x:=Yx.xx]) = (Yx.xx)(Yx.xx)

LC- 变量【闭包？】

自由和绑定变量
– Y操作符内的是被绑定的,外部的是自由变量.
– 比如,y是绑定的,x是自由的:
● Yy.x x y
– 绑定按照最近原则
● Yx.y(Yx.z x) 最后的x绑定的是第二个.
● 变量集的定义:
– FV(x)={x} , x is a variable
– FV(Yx.M)=FV(M)/{x}
– FV(M N)=FV(M)∪FV(N)
● 没有自由变量的表达式是closed的.也即组合子或者是组合逻辑中的表达式

LC- 三个转换

也叫alpha-renaming,绑定的变量可以随时改变名称.
– 通过alpha变换的表达式都是alpha-equivalent，static scope的语言[比
如c,cpp],只要保证变量名称不掩盖scope中原有的就可以了.
– 代换中的使用就需要alpha来防止不必要的歧义.
● β-reduction
– 函数求值
– ((Yv.e)e') is e[v:=e'e],举例是((Yn.n*2)7) -> 7*2
● η-conversion
– 用于表示两个函数的相等性
– 此变换用于化简,不是必须的.

church encoding

Church Numerals
– 对自然数的建模
● Church Booleans
– 逻辑
● Church pairs
– List 基本操作的影子
● List encodings
● 递归
● ......

函数是通过λ表达式匿名地定义的，这个表达式说明了此函数将对其参数进行什么操作。例如，“加2”函数f(x)= x + 2可以用lambda演算表示为λx.x + 2 (或者λy.y + 2，参数的取名无关紧要)而f(3)的值可以写作(λx.x + 2) 3。函数的应用（application）是左结合的：f x y =(f x) y。

考虑这么一个函数：它把一个函数作为参数，这个函数将被作用在3上：λf.f 3。如果把这个（用函数作参数的）函数作用于我们先前的“加2”函数上：(λf.f 3)(λx.x+2)，则明显地，下述三个表达式：

(λf.f 3)(λx.x+2) 与 (λx.x + 2) 3 与 3 + 2

是等价的。有两个参数的函数可以通过lambda演算这么表达：一个单一参数的函数的返回值又是一个单一参数的函数（参见Currying）。例如，函数f(x, y) = x - y可以写作λx.λy.x - y。下述三个表达式：

(λx.λy.x - y) 7 2 与 (λy.7 - y) 2 与 7 - 2

也是等价的。然而这种lambda表达式之间的等价性无法找到一个通用的函数来判定。

并非所有的lambda表达式都可以规约至上述那样的确定值，考虑

(λx.x x)(λx.x x)

或

(λx.x x x)(λx.x x x)

然后试图把第一个函数作用在它的参数上。 (λx.x x)被称为ω 组合子，((λx.x x)(λx.x x))被称为Ω，而((λx.x x x) (λx.x x x))被称为Ω₂，以此类推。(欧米伽Ω Omega（大写Ω，小写ω ），又称为大O，)

若仅形式化函数作用的概念而不允许lambda表达式，就得到了组合子逻辑。

类似λx.(x y)这样的lambda表达式并未定义一个函数，因为变量y的出现是自由的，即它并没有被绑定到表达式中的任何一个λ上。一个lambda表达式的自由变量的集合是通过下述规则（基于lambda表达式的结构归纳地）定义的：

在表达式V中，V是变量，则这个表达式里自由变量的集合只有V。
在表达式λV .E中（V是变量，E是另一个表达式），自由变量的集合是E中自由变量的集合减去变量V。因而，E中那些V被称为绑定在λ上。
在表达式 (E E')中，自由变量的集合是E和E'中自由变量集合的并集。

在lambda表达式的集合上定义了一个等价关系(在此用==标注)，“两个表达式其实表示的是同一个函数”这样的直觉性判断即由此表述，这种等价关系是通过所谓的“alpha-变换规则”和“beta-归约规则”。

α-变换[编辑]

Alpha-变换规则表达的是，被绑定变量的名称是不重要的。比如说λx.x和λy.y是同一个函数。尽管如此，这条规则并非像它看起来这么简单，关于被绑定的变量能否由另一个替换有一系列的限制。

Alpha-变换规则陈述的是，若V与W均为变量，E是一个lambda表达式，同时E[V:=W]是指把表达式E中的所有的V的自由出现都替换为W，那么在W不是 E中的一个自由出现，且如果W替换了V，W不会被E中的λ绑定的情况下，有

λV.E == λW.E[V:=W]

这条规则告诉我们，例如λx.(λx.x) x这样的表达式和λy.(λx.x) y是一样的。

β-归约[编辑]

Beta-归约规则表达的是函数作用的概念。它陈述了若所有的E'的自由出现在E [V:=E']中仍然是自由的情况下，有

((λV.E) E') == E [V:=E']

成立。

==关系被定义为满足上述两条规则的最小等价关系（即在这个等价关系中减去任何一个映射，它将不再是一个等价关系）。

对上述等价关系的一个更具操作性的定义可以这样获得：只允许从左至右来应用规则。不允许任何beta归约的lambda表达式被称为Beta范式。并非所有的lambda表达式都存在与之等价的范式，若存在，则对于相同的形式参数命名而言是唯一的。此外，有一个算法用户计算范式，不断地把最左边的形式参数替换为实际参数，直到无法再作任何可能的规约为止。这个算法当且仅当lambda表达式存在一个范式时才会停止。Church-Rosser定理说明了，当且仅当两个表达式等价时，它们会在形式参数换名后得到同一个范式。

η-变换

前两条规则之后，还可以加入第三条规则，eta-变换，来形成一个新的等价关系。Eta-变换表达的是外延性的概念，在这里外延性指的是，两个函数对于所有的参数得到的结果都一致，当且仅当它们是同一个函数。Eta-变换可以令λx .f x和f相互转换，只要x不是f中的自由出现。下面说明了为何这条规则和外延性是等价的：

若f与g外延地等价，即，f a == g a对所有的lambda表达式a成立，则当取a为在f中不是自由出现的变量x时，我们有f x == g x，因此λx .f x == λx .g x，由eta-变换f == g。所以只要eta-变换是有效的，会得到外延性也是有效的。

相反地，若外延性是有效的，则由beta-归约，对所有的y有(λx .f x) y == f y，可得λx .f x == f，即eta-变换也是有效的。

Natural Numbers as Church Numerals
----------------------------------

Natural numbers are non-negative. Given a successor function, next, 
which adds one, we can define the natural numbers in terms of
zero and next:

    1 = (next 0)
    2 = (next 1)
      = (next (next 0))
    3 = (next 2)
      = (next (next (next 0)))

and so on. Therefore a number n will be that number of
successors of zero. Just as we adopted the convention TRUE = first,
and FALSE = second, we adopt the following convention:

     zero  = Lf.Lx.x
     one   = Lf.Lx.(f x)
     two   = Lf.Lx.(f (f x))
     three = Lf.Lx.(f (f (f x)))
     four  = Lf.Lx.(F (f (f (f x))))


Therefore we have a "unary" representation of the natural
numbers, such that n is represented as n applications of the
function f to the argument x. This representation is refered to as
CHURCH NUMERALS. 

We can define the function next as follows:

  next = Ln.Lf.Lx.(f ((n f) x))

and therefore one as follows:

 next = Ln.Lf.Lx.(f ((n f) x))

and therefore one as follows:

  one = (next zero)
      => (Ln.Lf.Lx.(f ((n f) x)) zero)
      => Lf.Lx.(f ((zero f) x))
      => Lf.Lx.(f ((Lg.Ly.y f) x)) (* alpha conversion avoids clash *)
      => Lf.Lx.(f (Ly.y x))
      => Lf.Lx.(f x)

and two as follows:

  two = (next one)
      => (Ln.Lf.Lx.(f ((n f) x)) one)
      => Lf.Lx.(f ((one f) x))
      => Lf.Lx.(f ((Lg.Ly.(g y) f) x)) (* again, alpha conversion *)
      => Lf.Lx.(f (Ly.(f y) x)
      => Lf.Lx.(f (f x))

val next = fn n => fn f => fn x => (f ((n f) x));

NOTE that ((two g) y) = (g (g y)). So if we had some function, say
one that increments n:
 
   inc = Ln.(n+1)

then we can get a feel for a Church Numeral as follows:

   ((two inc) 0)
   => ((Lf.Lx.(f (f x)) inc) 0)
   => (Lx.(inc (inc x) 0)
   => (inc (inc 0))
   => (Ln.(n+1) (Ln.(n+1) 0))
   => (Ln.(n+1) (0 + 1))
   => ((0 + 1) + 1)
   => 2

We are now in a position to define addition in terms of next:

   add = Lm.Ln.Lf.Lx.((((m next) n) f) x);

Therefore four may be computed as follows:

   four = ((add two) two)
        => ((Lm.Ln.Lf.Lx.((((m next) n) f) x) two) two)
        => (Ln.Lf.Lx.((((two next) n) f) x)
        => Lf.Lx.((((two next) two) f x)
        => Lf.Lx.((((Lg.Ly.(g (g y)) next) two) f x)
        => Lf.Lx.(((Ly.(next (next y)) two) f) x)
        => Lf.Lx.(((next (next two)) f) x)
        => Lf.Lx.(((next (Ln.Lf.Lx.(f ((n f) x)) two)) f) x)


Multiplication is defined as follows:

   mult = Lm.Ln.Lx.(m (n x))

   six  = ((mult two) three)
        => ((Lm.Ln.Lx.(m (n x)) two) three)
        => (Ln.Lx.(two (n x) three)
        => Lx.(two (three x))
        => Lx.(two (Lg.Ly.(g (g (g y))) x))
        => Lx.(two Ly.(x (x (x y))))
        => Lx.(Lf.Lz.(f (f z)) Ly.(x (x (x y))))
        => Lx.Lz.(Ly.(x (x (x y))) (Ly.(x (x (x y))) z))
        => Lx.Lz.(Ly.(x (x (x y))) (x (x (x z))))
        => Lx.Lz.(x (x (x (x (x (x z))))))


And exponentiation as follows:

    power = Lm.Ln.(m n);

    nine  = ((power two) three)
          => ((Lm.Ln.(m n) two) three)
          => (Ln.(two n) three)
          => (two three)
          => (Lf.Lx.(f (f x)) three)
          => Lx. (three (three x))
          => Lx. (three (Lg.Ly.(g (g (g y))) x))
          => Lx. (three Ly.(x (x (x y))))
          => Lx. (Lg.Lz.(g (g (g z))) Ly.(x (x (x y))))
          => Lx.Lz.(Ly.(x (x (x y))) 
                    (Ly.(x (x (x y)))
                     (Ly.(x (x (x y))) z)))
          => Lx.Lz.(Ly.(x (x (x y)))
                    (Ly.(x (x (x y)))
                      (x (x (x z)))))
          => Lx.Lz.(Ly.(x (x (x y)))
                     (x (x (x (x (x (x z)))))))
          => Lx.Lz.(x (x (x (x (x (x (x (x (x z)))))))))


The following lambda function tests for zero:

   third = Lx.Ly.Lz.z
   iszero = Ln.((n third) first)

Another approach:

   T = Lx.Ly.x
   F = Lx.Ly.y
   af = Lx.F
   zp = Ln.((n af) T)

Here we take a function "af" that always returns "false".
Since a church numeral is a function of two arguments, we
apply the number to be tested to "af" as the first argument 
and to "T" as the second argument.  

If the number being tested is zero (which is the same as "F"), then 
it selects the second argument and so returns "T".

If the number is not zero then it will behave as a church
numeral and apply the function some number of times...
and the function it applies is a function that returns "F" in all
circumstances... no matter how many times it's applications are nested.

Let's try this for a test of two:

(zp two)  -->  (L n ((n af) T) two) --> ((two af) T)
          -->  ( (L g L y (g (g y)) af) T )
          -->  ( L y (af (af y)) T )
          -->  ( af ( af T ) )
          -->  ( L x F ( L x F T ) )
          -->  F


The lambda function pred delivers the predecessor of a
Church Numeral:


    pair = Lx.Ly.Lf.((f x) y);
    prefn = Lf.Lp.((pair (f (p first))) (p first))
    pred = Ln.Lf.Lx.(((n (prefn f)) (pair x x)) second)

   
It should be of interest to note the following. A major
landmark in Lambda Calculus occurred in the 1930's when
Kleene discovered how to express the operation of
subtraction within Church's scheme (yes, that means that even
though Church invented/discovered the Lambda Calculus he was
unable to implement subtraction and subsequently division, within
that calculus)! Other landmarks then followed, such as the recursive 
function Y. In 1937 Church and Turing, independently, showed that every 
computable operation (algorithm) can be achieved in a Turing machine
and in the Lambda Calculus, and therefore the two are equivalent.  
Similarly Godel introduced his description of computability, again 
independently, in 1929, using a third approach which was again shown 
to be equivalent to the other 2 schemes.

It appears that there is a "platonic reality" about
computability. That is, it was "discovered" (3 times idepenedently)
rather than "invented". It appears to be natural in some
sense.


(********************** ml source ***********************)

(* Church Numerals *)

val zero = fn f => fn x => x;
val next = fn n => fn f => fn x => (f ((n f) x));
val add = fn m => fn n => fn f => fn x => ((((m next) n) f) x);
val mult = fn f => fn g => fn x => (f (g x));
val power = fn f => fn g => (f g);

(* Church Numerals *)
val one = (next zero);
val two = (next one);

val inc = fn n => n+1;

(* More Church Numerals *)
val four = (add one (add one (add one (add one zero))));
val three = ((add one) two);
val five = ((add three) two);
val six = ((mult three) two);
val nine = ((power two) three);
val ten = ((mult two) five);

(* A test to show what a Church Numeral does *)

((zero inc) 0);
((five inc) 0);
((ten inc) 0);

val first = fn x => fn y => x;
val second = fn x => fn y => y;
val third = fn x => fn y => fn z => z;

val iszero = fn n => ((n third) first);
(* Predicate, is a Church Numeral zero? *)

val T = fn x => fn y => x ;
val F = fn x => fn y => y ;
val af = fn x => F;
val zp = fn n => ((n af) T);  (* zp is a zero predicate *)

val pair = fn x => fn y => fn f => ((f x) y);

val prefn = fn f => fn p => ((pair (f (p first))) (p first));
val pred = fn n => fn f => fn x => (((n (prefn f))(pair x x)) second);
(* predecessor function *)

val eight = (pred nine);

转自：http://www.cs.unc.edu/~stotts/723/Lambda/church.html

http://blog.csdn.net/crazyhacking/article/details/8183088

更多：https://gist.github.com/vivekhaldar/2438498

http://jtauber.com/blog/2008/11/26/church_encoding_in_python/