笔者,特别地对归并排序的
复杂度进行了分析;
看了好多博客,只是简单的说了下结论,结论怎么来的,根本不去分析,写博客跟没写似的,,更气人的是,还有抄书的,书上写啥,博客就写啥,浪费时间,这种博客,写的人、看的人,时间都被浪费了;
目录
归并排序
先了解下归并排序中归并的意思;
归并:即将两个有序的数组,合并为一个更大的有序的数组 ;
思想:要想将一个大数组排序,我们可以将大数组分为两个小的数组,对这个小的数组进行排序,然后将两个小的有序的数组,归并 到一个大的数组中;递归 这个过程,直到小的数组中元素 只有一个,然后进行归并;
缺点(使用‘原地归并’解决)
从上面的 思想 里面,我们可以知道,归并排序 是一个使用 递归 的排序算法;而说到递归,就会想到每次递归需要的 空间;
就像我们上面说的一样,每次归并两个小数组的时候,都创建一个新的数组(申请新的内存空间),将归并的结果放到里面;这样做,当需要进行排序的数组的长度,很小的时候,没有什么问题;
但是,需要排序的数组的长度很大的时候,我们需要递归的次数,也就随之变多,这样一个递归排序需要的空间,就急剧增加,是我们不能忍受的 ;
这里我们可以将使用的空间降低到最低,就是每次递归,进行归并两个小的数组的时候,我们并不创建新的数组,来存储归并的结果 ;而是在递归开始的时候,创建一个跟需要排序的数组一样大的数组,在每次递归的时候,先把两个小数组里面的元素,复制进这个大数组里面,而将归并的结果,放回小数组里面;这样,就避免了,每次递归都创建数组的缺点 ;
但是,还是避免不了最少使用 N 个额外的数组空间 ;这里的原地,并不是真正的原地 ;还是需要最少 N 个额外空间 ;
上述思想是一种
原地排序的思想;
java代码实现
归并排序有两种实现方式,这是其一:自顶向下的归并排序
package cn.yaz.study.sort._2_2;
import cn.yaz.study.sort._2_1.Example;
import org.junit.Test;
/**
* 归并排序(自顶向下的归并排序)
*/
public class Merge {
@Test
public void test(){
Integer[] a = {3, 2, 1, 6, 34, 2, 12, 55, 334, 56, 2, 78,12,45,25};
sort(a);
Example.show(a);
}
// 辅助数组。所有归并需要的暂用空间,由它提供
public Comparable[] c;
public void sort(Comparable[] comparable) {
// 创建辅助数组
c = new Comparable[comparable.length];
// 进行归并排序
sort(comparable, 0, comparable.length - 1);
}
/**
* 归并排序的递归代码
*/
public void sort(Comparable[] comparables, int lo, int hi) {
// 先判断小数组的长度
if (lo >= hi) {
return;
}
// 继续递归,将每一个小数组,再次一分为二
// 将左半边数组排序
sort(comparables, lo, (lo + hi) / 2);
// 将右半边数组排序
sort(comparables, (lo + hi) / 2 + 1, hi);
// 小数组各自排序完毕。进行归并
merge(comparables, lo, hi);
}
/**
* 归并代码
*/
public void merge(Comparable[] comparables, int lo, int hi) {
// 先将需要归并的小数组,复制到辅助数组里面
for (int i = lo; i <= hi; i++) {
c[i] = comparables[i];
}
// 右半边数组的起始角标
int rStart = (lo + hi) / 2 + 1;
// 记录下这个其实角标
int mid = rStart;
// 因为下面我们需要单独操作数组c、comparables ;因此,我们再准备一套角标
// lo、hi 操作 comparables数组; i、j 操作 c 数组
int i = lo;
int j = hi;
// 进行归并
while (lo <= hi) {
// 需要重点注意的事情:下面的if语句的顺序,是不可以随便写的
// 也就是判断小数组是个归并结束的代码,要放在数组元素比较之前;
// 表示左半个数组,归并完事了,可以将右边数组剩下元素,直接插入了
if (i == mid) {
comparables[lo++] = c[rStart++];
// 剩下的最后一种情况,就是右半个数组,归并完事了,可以将左边数组剩下元素,直接插入了
} else if (rStart == j + 1) {
comparables[lo++] = c[i++];
}
// 如果 c[i] < c[rStart],小的元素,归并进 comparables 数组中
else if (Example.less(c[i], c[rStart])) {
// 赋值的同时,完成 i 指向下一个数组元素
comparables[lo++] = c[i++];
}
// 如果 c[i] > c[rStart],小的元素,归并进 comparables 数组中
else if (!Example.less(c[i], c[rStart])) {
// 赋值的同时,完成 i 指向下一个数组元素
comparables[lo++] = c[rStart++];
}
}
}
}Example类,请见 ;
复杂度分析
我看了好多博客,根本不对复杂度进行分析,只是直接写出结论,没意思;
先分析 比较次数
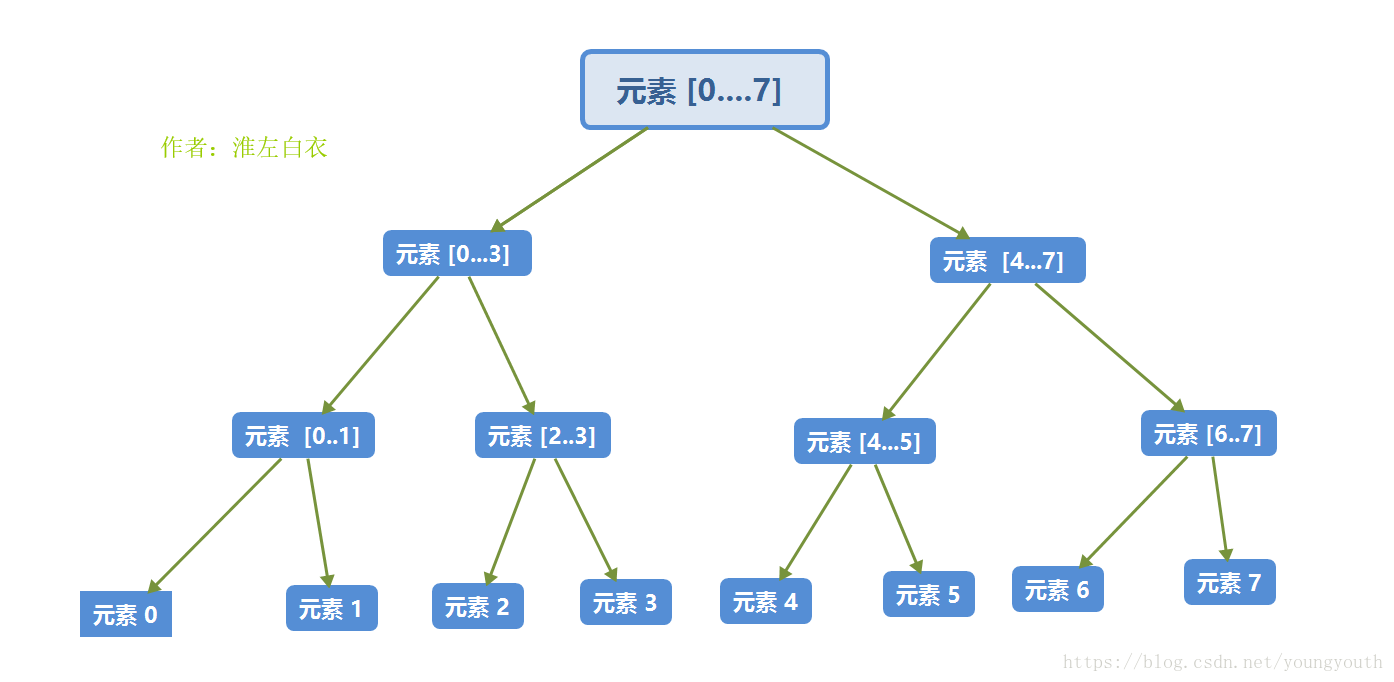
递归树
(K从0开始计数)第K层,有 个子数组 ;每个子数组有 个元素,对于有 个元素的数组,最多需要比较 次;第 K 层,需要 x = 次比较;( n = N是数组元素的总数,因此,这里也就是 N 次比较 ;)
这里说的,都是书上的话,看了也不定记得!反正笔者是没记住
擦!正在我苦苦思索,怎么用语言把比较次数直白的、简单的、容易记住的 描述出来的时候,我突然发现,递归树,每层元素都是一样多的,都是N个元素,而我们为N个元素进行排序的时候,最多需要N次比较;so,只要知道递归树有多少层就可以求出一共比较了多少次了;很容易推导出,N 个元素的数组的 二分递归树 一共有 层(根节点除外,学过高中数学就可以推导出)
因此一共比较了 N x = N 次;
上述说的比较次数是最坏情况下,因为,数组的个数是2的幂,此时递归树是一个完全二叉树;
假如,数组的不是2的幂,则 递归树,将不是 一个完全二叉树,最后一层的元素,就将比 N 少,因此,最后一层的比较次数,比 N 少;
因此,总体上是 小于 N 次
再分析 访问数组次数
我另辟蹊径,还是从,递归树,每层元素都是一样多的,都是N个元素,这个角度入手
访问数组的操作,只发生在 merge( ) 方法里面,而递归树的每层的每一个元素,都是要经过 merge( ) 方法的,在 merge( ) 方法里面,N 个元素,需要 N 次 复制,N 次赋值,最多需要 N 次比较,我们在 merge( ) ,一共有 两个数组 ,每次访问都是一起访问,因此,访问数组 3N x 2 = 6N 次,而我们一共有 层;
因此,一共访问 6N 次数组 ;
master定理
对于这种递归的复杂度,找不到合理的方法,干推,太闹心了,如果不想推导,可以直接使用 master定理 ;
master定理
递归关系: T(n) = a*T(n/b)+c*n^k ;T(1) = c ;有这样的结论:
if (a > b^k)——T(n) = O(n^(logb(a)))if (a = b^k)——T(n) = O(n^k*logn)if (a < b^k)——T(n) = O(n^k)
sort(comparables, lo, (lo + hi) / 2); //
sort(comparables, (lo + hi) / 2 + 1, hi);
merge(comparables, lo, hi);
我们写的代码的 递归状态方程:这里又需要写出 递归状态方程 。。。。。不写了!(感兴趣的同学,自己去看专门介绍 master定理 的博客,这里我还是重点讲 归并排序 的)
改进
算法第四版的课后作业,有下面的题,我会把代码放到我写的
《算法第四版-课后习题答案》,里面,需要的同学,可以去查看下 ;
我们可以对上述的代码,进行改进,提高归并排序的性能 ;
对小规模数组使用
插入排序理由:当我们进行递归二数组的时候,如果当小数组的长度,已经不是很大的时候,依然使用递归继续二分的话,那么,我们将频繁的调用merge()方法;这也是递归固有的通病:当
子问题规模很小的时候,,递归会使得调用过于频繁 ;因此,我们可以考虑,当小数组的长度小于一定长度(书上建议为15)的时候,使用
插入排序,来对小数组进行排序,可以提高插入排序的性能 ;因为
插入排序对 小规模乱序数组(满足插入排序适用场景之一:每个元素距离它最终的位置都不远;) 排序很快;每次归并之前,测试两个小数组,是否有序
理由:如果两个小数组满足[mid] < [mid+1],也就是说,左边的小数组的最后一个元素,小于右边小数组的第一个元素;那么这两个小数组,是可以直接归并进大数组里面的,这样就省却了每次都比较的开销 ;每次归并的时候,不将数组复制到辅助数组里面
理由: 我们可以不用把数组复制到辅助数组里面,再排序回原数组中 ;其实,可以让辅助数组、原数组的角色,来回交替变化,达到完成排序,而不复制的效果 ;
上述改动,均可见代码:
归并排序的意义
我们前面学过的排序算法,复杂度都是指数级别的,今天学的归并排序,将复杂度降低到了,对数级别;这是一个很有意义的算法,让我们在对非常大多的数据量进行排序,变为可能;
但是,归并排序并不是完美的,它有一个缺点,就是需要 N 个额外空间的辅助数组,来辅助排序,并不是原地排序 ;
下次讲的 快速排序,则可以克服掉 归并排序 的 缺点 ;