啦啦啦我ysw又回来啦!之后大概会准备打acm,暑假尽量复习复习,因为已经快两年没碰oi了,最多也就高三noip前学弟学妹出题讲题,所以从这一篇blog开始大概会有一系列“打基础”的blog,既是复习也是重新学一遍叭~高中的时候学得就不太扎实
题意:对于一个任何三条对角线不会交于同一点的凸$n$边形,问对角线交点个数,$nleq 10^5$。
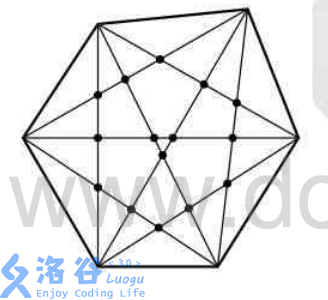
例如$n=6$的情形下答案为15

似乎我们可以随意给一个端点编号为1,按照逆时针/顺时针顺序依次编号$1,2,3……n$,这样一来我们可以先只考虑以点1为其中一个端点出发的所有对角线(图中红线)对应的交点,这个问题似乎好处理了许多,因为如果另一条对角线要和它有交点(蓝线)当且仅当蓝线的两个端点在红线的两侧!(嗯!这不就是计算几何里面判断直线是否有交点的方法嘛!?)
于是我们想,对于编号为$k$的点,1~k内从点2到点$k-1$是可以作为其中一个起点的,一共是$k-1-2+1=k-2$个点,同样的另一侧从$k+1$到$n$可以作为对角线另一点,一共是$n-(k+1)+1=n-k$个点
乘法原理得到$(k-2)(n-k)$,接着只要对所有情形进行求和就行了,对于$k$来说最小取到3(2的话就不是对角线了),最大取到$n-1$
所以对于以任意一点为端点的所有对角线的交点便是:$m=sum_{k=3}^{n-1}(n-k)(k-2)$,对$n$个点进行同样的操作就得到$nm$,而注意到如果这样写,每个交点对应两条对角线的四个端点都作为了一次起点,也就是说每个交点都被算了四次,所以我们要的答案应该是$ans=frac{1}{4}nm$,式子推出来啦!
接着就可以编程求解了…首先整个问题的时间复杂度是$O(n)$,轻轻松松通过,不过我们注意到对应答案的上界是$O(n^3)$级别的也就是$10^{15}$级别的差不多,一开始我只开了个long long交上去然后挂了两个点…后面改成unsigned long long 就过了…emm好吧
话说回来我们再回头看看那个和式$m=sum_{k=3}^{n-1}(n-k)(k-2)$,好像我们并不陌生呀!
里面展开就是$nk-2n-k^2-2k$我们对k求和就稍微整理一下变成$sum_{k=3}^{n-1}[k(n-2)-2n-k^2]$,嗯第一项是等差数列,第二项是对于$k$的常数列,第三项是平方和,我们有结论$sum_{k=1}^{n}k^2=frac{1}{6}n(n+1)(2n+1)$,对于这题只要改个$n$再扣掉前两项就行
整个和式拆开再化简就得到这题的答案可以写成:
$frac{n}{4}[frac{1}{2}(n+2)^2-2(n^2-3n)-frac{1}{6}n(n-1)(2n-1)+5]$
整个问题变成$O(1)$的复杂度啦!~(虽然好像没什么用,哈哈哈)